Integral dengan Batas Tak Hingga
Integral tentu yang kita pelajari awalnya adalah mengintegralkan fungsi f(x) pada interval yang jelas, yaitu [a, b]. Dalam banyak situasi nyata, terutama di bidang seperti fisika, ekonomi, dan statistik, kita seringkali ingin mengintegralkan fungsi pada interval yang tidak terbatas. Misalnya, dari 0 hingga ∞, atau dari −∞ hingga plus tak hingga. Integral seperti ini disebut integral tak wajar. Istilah "batas tak hingga" mengacu pada fakta bahwa kita membiarkan salah satu atau kedua batas integral menuju tak hingga (positif atau negatif). Ini berarti kita sedang mencari luas di bawah kurva yang meluas hingga tak terhingga. Karena kita tidak bisa benar-benar menghitung hingga tak hingga, kita perlu mengembangkan konsep limit untuk memberikan makna pada integral tak wajar. Kita akan melihat bagaimana nilai integral mendekati suatu angka tertentu saat batas atas atau bawah mendekati tak hingga.
Integral tak wajar sangat penting dalam banyak aplikasi karena memungkinkan kita untuk menghitung kuantitas yang melibatkan proses yang berlanjut tanpa batas. Misalnya, dalam probabilitas, kita seringkali ingin menghitung peluang suatu peristiwa terjadi dalam rentang nilai yang sangat besar. Integral tak wajar adalah perluasan dari konsep integral tertentu. Mereka memungkinkan kita untuk menghitung luas di bawah kurva pada interval yang tidak terbatas. Meskipun konsepnya mungkin terlihat rumit pada awalnya, integral tak wajar adalah alat yang sangat kuat dalam banyak bidang ilmu.
1. Integral dengan Satu Batas Tak Hingga
Jika nilai limitnya ada dan nilainya terbatas (bukan ±∞), maka kita katakan bahwa integral tak wajar yang bersesuaian konvergen dan memiliki nilai tersebut. Jika tidak, integral dikatakan divergen.
Konvergen: Jika ketika kita mendekati batas tak hingga, nilai integral mendekati suatu bilangan tertentu (dan bilangan itu bukan tak hingga), maka kita katakan integral tersebut konvergen. Artinya, integral memiliki nilai yang jelas.
Divergen: Jika nilai integral tidak mendekati bilangan tertentu ketika kita mendekati batas tak hingga (misalnya, nilai integral terus bertambah besar tanpa batas), maka kita katakan integral tersebut divergen. Artinya, integral tidak memiliki nilai yang jelas.
contoh:
Misal diberikan fungsi f(x) = xe-x. Tentu saja mengintegralkan f(x) pada interval [0, 1] atau [0, 2] dapat dengan mudah dilakukan. Misal f(x) diintegralkan pada interval [0, b] dengan b > 0 akan menjadi:
2. Integral dengan Kedua Batasnya Tak Hingga
3. Fungsi Densitas
Misalkan X adalah suatu variabel random kontinu. Fungsi 𝑓(𝑥) = P(X = 𝑥) disebut fungsi densitas variabel random X jika dan hanya jika:
Nilai mean dan varians variabel random kontinu didefinisikan sebagai:
Nilai fungsi tidak pernah negatif, dan
Untuk x < 0, jelas bahwa F(x) = P(X ≤ x) = 0. Adapun untuk x ≥ 0:
sehingga fungsi distribusi kumulatifnya adalah:
d) Misal 𝜆 = 0,01; tentukan peluang bahwa masa hidupnya lebih dari 20 jam!
d) Misal 𝜆 = 0,01; tentukan peluang bahwa masa hidupnya lebih dari 20 jam!
Misal kurva y = 1/x pada interval [1, ∞) diputar mengelilingi sumbu-x, terbentuklah benda putar yang dinamai sebagai "Gabriel's Horn". Kita mengklaim bahwa:
1. Volume V dari benda ini adalah terbatas (finite);
2. Luas permukaan A dari benda ini adalah tak terbatas (infinite).
Jika kita coba terapkan dalam kehidupan sehari-hari, hasil ini seolah-olah mengatakan bahwa benda tersebut dapat diisi dengan sejumlah cat yang terbatas, namun tidak cukup cat untuk mengecat seluruh permukaan bagian dalamnya. Berikut perhitungan volume dan luasnya:
Adapun luas permukaannya tak hingga.
Paradoks Gabriel's Horn adalah sebuah konsep dalam kalkulus yang cukup membingungkan. Bayangkan sebuah bentuk seperti terompet yang ujungnya semakin mengecil hingga tak terhingga. Paradoks ini menyatakan bahwa bagian dalam terompet ini dapat diisi dengan cat dalam jumlah yang terbatas, namun luas permukaan bagian dalamnya justru tak terhingga. Intuisi kita mungkin akan mengatakan bahwa jika luas permukaan suatu benda tak terhingga, maka volume benda tersebut juga harus tak terhingga. Namun, dalam kasus Gabriel's Horn, perhitungan matematis menunjukkan hasil yang berbeda. Paradoks ini muncul karena sifat-sifat khusus dari fungsi yang digunakan untuk membentuk Gabriel's Horn (y = 1/x). Ketika kita memutar fungsi ini mengelilingi sumbu x, kita mendapatkan bentuk yang unik di mana volume mendekati nilai tertentu (terbatas) saat panjang terompet mendekati tak hingga, namun luas permukaannya terus bertambah tanpa batas. Meskipun terdengar kontraintuitif, paradoks ini memiliki implikasi dalam berbagai bidang, seperti fisika dan matematika. Konsep ini membantu kita memahami bagaimana konsep volume dan luas permukaan dapat berperilaku secara berbeda dalam situasi tertentu. Paradoks Tanduk Gabriel adalah sebuah konsep matematis yang menunjukkan bahwa sebuah benda dapat memiliki volume yang terbatas namun luas permukaan yang tak terbatas. Konsep ini sering digunakan sebagai contoh menarik untuk menunjukkan bagaimana intuisi kita terkadang dapat bertentangan dengan hasil perhitungan matematis.
Paradoks Gabriel's Horn adalah sebuah konsep dalam kalkulus yang cukup membingungkan. Bayangkan sebuah bentuk seperti terompet yang ujungnya semakin mengecil hingga tak terhingga. Paradoks ini menyatakan bahwa bagian dalam terompet ini dapat diisi dengan cat dalam jumlah yang terbatas, namun luas permukaan bagian dalamnya justru tak terhingga. Intuisi kita mungkin akan mengatakan bahwa jika luas permukaan suatu benda tak terhingga, maka volume benda tersebut juga harus tak terhingga. Namun, dalam kasus Gabriel's Horn, perhitungan matematis menunjukkan hasil yang berbeda. Paradoks ini muncul karena sifat-sifat khusus dari fungsi yang digunakan untuk membentuk Gabriel's Horn (y = 1/x). Ketika kita memutar fungsi ini mengelilingi sumbu x, kita mendapatkan bentuk yang unik di mana volume mendekati nilai tertentu (terbatas) saat panjang terompet mendekati tak hingga, namun luas permukaannya terus bertambah tanpa batas. Meskipun terdengar kontraintuitif, paradoks ini memiliki implikasi dalam berbagai bidang, seperti fisika dan matematika. Konsep ini membantu kita memahami bagaimana konsep volume dan luas permukaan dapat berperilaku secara berbeda dalam situasi tertentu. Paradoks Tanduk Gabriel adalah sebuah konsep matematis yang menunjukkan bahwa sebuah benda dapat memiliki volume yang terbatas namun luas permukaan yang tak terbatas. Konsep ini sering digunakan sebagai contoh menarik untuk menunjukkan bagaimana intuisi kita terkadang dapat bertentangan dengan hasil perhitungan matematis.
Apakah ada yang salah dengan matematika kita? Tidak. Bayangkan tanduk itu dibelah di sisi, dibuka, lalu dibentangkan. Dengan jumlah cat yang terbatas, kita tidak mungkin mengecat permukaan ini dengan lapisan cat yang ketebalannya seragam. Namun, kita bisa melakukannya jika kita mengijinkan lapisan cat menjadi semakin tipis saat kita bergerak semakin jauh dari ujung tebal tanduk. Dan tentu saja, itulah yang terjadi ketika kita mengisi tanduk yang tidak dibelah dengan π satuan kubik cat.
5. Integral Tak Hingga Fungsi Pangkat
Pada kasus Gabriel's Horn, telah diketahui bahwa integral ini divergen untuk p = 1, untuk p < 1 juga divergen, adapun untuk p > 1 integral ini konvergen.


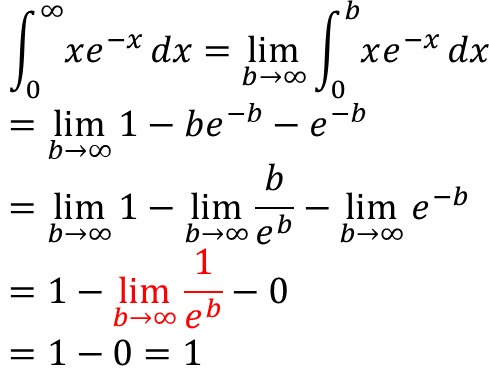









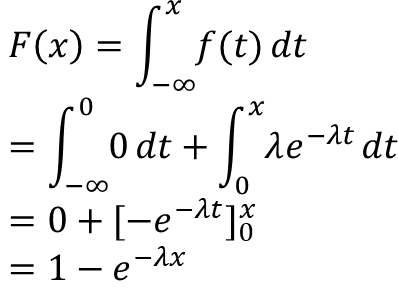
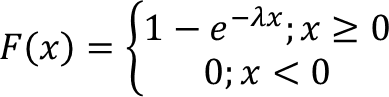




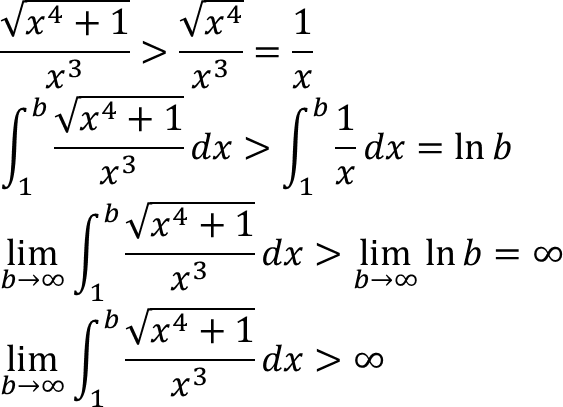
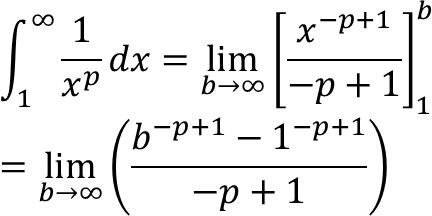
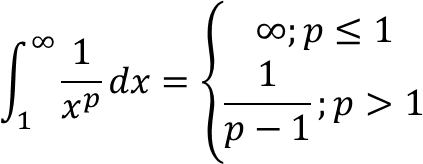


Komentar
Posting Komentar