Uji Linearitas dan Keberartian Regresi
1. Uji Linearitas Regresi
➢ Analisis regresi mengharuskan adanya hubungan fungsional antara X dan Y yang linear → perubahan nilai di salah satu variabel independen akan menghasilkan perubahan yang konstan pada variabel dependen.
➢ Tujuan linearitas pada regresi adalah meyakinkan hubungan linear pada X dan Y dan juga dampak dari model tersebut. Selain itu, residu tersisa sudah tidak memiliki pola tertentu sehingga memastikan bahwa model yang dikeluarkan benar tepat.
➢ Tidak dipenuhinya asumsi linearitas menjadikan estimasi parameter regresi menjadi bias (koefisien regresi, kesalahan baku, dan pengujian signifikansi) yang berakibat model regresi menjadi tidak tepat jika digunakan untuk prediksi.
➢ Hasil analisis regresi yang underfitting atau overfitting serta resiko kesalahan tipe I atau tipe II menjadi sangat besar.
Berikut langkah-langkah uji linearitas:
1. Urutkan dan Kelompokkan Data
Data diurutkan berdasarkan nilai X dari terkecil hingga terbesar. Data dengan nilai X yang sama dikelompokkan bersama.
X₁: Kelompok data dengan nilai X yang sama (X₁), memiliki n₁ data Y yang bersesuaian.
X₂: Kelompok data dengan nilai X yang sama (X₂), memiliki n₂ data Y yang bersesuaian.
⋮
Xk: Kelompok data dengan nilai X yang sama (Xk), memiliki nk data Y yang bersesuaian.
Total data (n) adalah jumlah dari semua pengulangan (n₁ + n₂ + ... + nk). 'k' menunjukkan kelompok data X yang unik atau berbeda.
2. Definisikan Istilah-istilah
Setelah data dikelompokkan, beberapa istilah didefinisikan untuk memudahkan perhitungan dan analisis selanjutnya:
Yij: Nilai Y yang ke-j dalam kelompok data Xᵢ. (j = 1, 2, ..., nᵢ). Artinya, ini adalah nilai Y individual dalam setiap kelompok X.
Tᵢ: Jumlah dari semua nilai Y dalam kelompok Xᵢ. (Tᵢ = Yᵢ₁ + Yᵢ₂ + ... + Yᵢnᵢ). Ini adalah total nilai Y untuk setiap kelompok X.
Ȳᵢ: Rata-rata nilai Y dalam kelompok Xᵢ. Dihitung dengan rumus: Ȳᵢ = Tᵢ / nᵢ (Total nilai Y dalam kelompok dibagi banyaknya data Y dalam kelompok tersebut).
3. Hitung Jumlah Kuadrat
a. Jumlah kuadrat regresi
b. Jumlah kuadrat galat
c. Jumlah kuadrat total
JKT = JKR + JKG
d. Jumlah kuadrat galat murni (variasi acak atau galat percobaan),
dengan dbGM = n – k
e. Jumlah kuadrat kekurangcocokan atau jumlah kuadrat tuna cocok (variasi yang menyimpang dari model)
𝐽𝐾𝐺𝑇𝐶 = 𝐽𝐾𝐺 − 𝐽𝐾𝐺𝑀 dengan dbGTC = 𝑘 − 2
4. Hitung Rerata Kuadrat
a. Rerata kuadrat galat murni, RKGM = JKGM/dbGM = JKGM/(n – k)
b. Rerata kuadrat galat tuna cocok, RKGTC = JKGTC/dbGTC = JKGTC/(k − 2)
5. Hitung Nilai F
F = RKGTM/RKGM
6. Tentukan keputusan berdasarkan daerah kritis:
DK = {F | F > Fα; k − 2; n – k}
Berikut tabel uji linearitas
|
SV |
JK |
db |
RK |
F |
|
Regresi |
JKR |
1 |
RKR |
|
|
Tuna Cocok |
JKGTC |
k – 2 |
RKGTC |
F = RKGTC/RKGM |
|
Galat Murni |
JKGM |
n – k |
RKGM |
|
|
Total |
JKT |
n – 1 |
|
|
Penelitian untuk mengetahui ada tidaknya hubungan antara variabel frekuensi penyiraman per pekan (x) dan kecepatan pertumbuhan tanaman (y) pada 10 kali eksperimen.
1. Hipotesis Statistik
H0: Hubungan antara X dan Y linear.
H1: Hubungan antara X dan Y tidak linear.
2. Taraf Signifikansi
α = 5% = 0,05
3. Statistik Uji
Ingat kembali pada artikel sebelumnya, bahwa persamaan regresinya adalah Y = 0,24 + 0,31X
JKT = 2,029
JKR = 1,922
JKG = 0,107
Selanjutnya untuk menghitung JKGM, JKGTC, RKGM, dan RKGTC digunakan tabel bantu sebagai berikut.
|
Kel |
X |
Y |
Y2 |
n |
T |
T2/n |
|
1 |
5 5 |
1,6 1,9 |
2,56 3,61 |
2 |
3,5 |
6,125 |
|
2 |
6 6 |
2,1 2,2 |
4,41 4,84 |
2 |
4,3 |
9,245 |
|
3 |
7 7 |
2,3 2,5 |
5,29 6,25 |
2 |
4,8 |
11,52 |
|
4 |
8 8 |
2,7 2,8 |
7,29 7,84 |
2 |
5,5 |
15,125 |
|
5 |
9 9 |
2,9 3,1 |
8,41 9,61 |
2 |
6 |
18 |
|
Total |
70 |
24,1 |
60,11 |
10 |
- |
60,015 |
Berdasarkan tabel di atas diperoleh nilai k = 5, jumlah kuadrat (JK) diperoleh sebagai berikut:
dbGTC = k − 2 = 5 − 2 = 3
Selanjutnya nilai Rerata Kuadrat (RK) sebagai berikut.
RKGM = JKGM/dbGM = 0,095/5 = 0,019
RKGTC = JKGTC/dbGTC = 0,012/3 = 0,004
F = RKGTC/RKGM = 0,004/0,019 = 0,210526
4. Daerah Kritis dan Keputusan Uji
DK = {F | F > Fα; k − 2; n – k} = {F | F > F0,05; 3; 5} = 5,409451
F = 0,210526 < 5,409451 sehingga F ∉ DK, akibatnya H0 diterima.
5. Kesimpulan
Hubungan antara X dan Y linear.
2. Uji Keberartian Regresi
➢ Uji keberartian atau signifikansi regresi digunakan untuk meyakinkan bahwa regresi yang didapat berdasarkan penelitian memiliki arti secara signikan → melihat keberartian (signifikansi) regresi.
Dalam pengujian keberartian regresi digunakan pendekatan analisis variansi dengan menggunakan nilai-nilai JKT, JKR, dan JKG yang sudah diperoleh sebelumnya seperti pada uji linearitas.
1. Hitung jumlah kuadrat
a. Jumlah kuadrat regresi
dengan dbR = 1
b. Jumlah kuadrat galat
dengan dbG = n − 2
c. Jumlah kuadrat total
JKT = JKR + JKG
dbT = dbR + dbG = n − 1
2. Hitung rerata kuadrat
a. Rerata kuadrat regresi
RKR = JKR/1 = JKR
b. Rerata kuadrat galat
RKG = JKG/dbG = JKG/(n − 2)
3. Hitung nilai F
F = RKR/RKG
4. Tentukan keputusan berdasarkan daerah kritis:
DK = {F | F > Fα; 1; n – 2}
Berikut tabel uji keberartian regresi
|
SV |
JK |
db |
RK |
F |
|
Regresi |
JKR |
1 |
RKR |
F = RKR/RKG |
|
Galat |
JKG |
n – 2 |
RKG |
|
|
Total |
JKT |
n – 1 |
|
|
Contoh:
Penelitian untuk mengetahui ada tidaknya hubungan antara variabel frekuensi penyiraman per pekan (x) dan kecepatan pertumbuhan tanaman (y) pada 10 kali eksperimen.
1. Hipotesis Statistik
H0: Hubungan antara X dan Y tidak berarti.
H1: Hubungan antara X dan Y berarti.
2. Taraf Signifikansi
α = 5% = 0,05
3. Statistik Uji
Ingat kembali pada artikel sebelumnya, bahwa persamaan regresinya adalah Y = 0,24 + 0,31X
JKT = 2,029
JKR = 1,922
dbR = 1
JKG = 0,107
dbG = n − 2 = 10 − 2 = 8
Selanjutnya nilai Rerata Kuadrat (RK) sebagai berikut.
RKR = JKR = 1,922
RKG = JKG/dbG = 0,107/8 = 0,013375
F = RKR/RKG = (1,922)/(0,013375) = 143,7009
4. Daerah Kritis dan Keputusan Uji
DK = {F | F > Fα; 1; n – 2} = {F | F > F0,05; 1; 8} = 5,317655
F = 143,7009 > 5,317655 sehingga F ∈ DK, akibatnya H0 ditolak dan H1 diterima.
5. Kesimpulan
Regresi linear antara X dan Y berarti.
3. Uji Keberartian Koefisien Regresi
Jika koefisien regresi berarti, maka dapat dikatakan terdapat pengaruh variabel X terhadap Y.
Ingat kembali rumus kesalahan baku koefisien regresi (b)
sedangkan kesalahan baku koefisien konstan (a)
Pengujian Keberartian Koefisien Regresi:
b: koefisien regresi
a: koefisien konstan
sb: kesalahan baku koefisien regresi
sa: kesalahan baku koefisien konstan
Adapun daerah kritis sebagai berikut.
Adapun daerah kritis sebagai berikut.
DK = {t | t < –t½α; n – 2 ∨ t > t½α; n – 2}
dengan t½α; n – 2 adalah nilai dari tabel t (distribusi student) dengan derajat kebebasan 𝑛 − 2.
Contoh:
1. Hipotesis Statistik
H0a: Koefisien konstan tidak berarti.
H1a: Koefisien konstan berarti.
H0b: Koefisien regresi tidak berarti.
H1b: Koefisien regresi berarti.
2. Taraf Signifikansi
α = 5% = 0,05
3. Statistik Uji
Ingat kembali pada artikel sebelumnya, bahwa persamaan regresinya adalah Y = 0,24 + 0,31X
a = 0,24 dan b = 0,31
ingat kembali bahwa JKG nya adalah 0,107; ∑x² = 510; n = 10; ∑x = 70
selanjutnya dihitung sa dan sb sebagai berikut.
4. Daerah Kritis dan Keputusan Uji
Titik kritis ±t½α; n – 2 = ±t0,025; 8 = ±2,306
DK = {t | t < –t½α; n – 2 ∨ t > t½α; n – 2} = {t | t < –2,306 ∨ t > 2,306}
ta = 7,037 > 2,306 sehingga ta ∈ DK, akibatnya H0a ditolak dan H1a diterima.
tb = 11,988 > 2,306 sehingga tb ∈ DK, akibatnya H0b ditolak dan H1b diterima.
5. Kesimpulan
Koefisien konstan dan koefisien regresi keduanya berarti. Dengan kata lain frekuensi penyiraman mempengaruhi kecepatan pertumbuhan.
Catatan:
Variabel bebas mempengaruhi variabel terikat atau tidak, bergantung pada keberartian koefisien regresi, terlepas koefisien konstan berarti atau tidak.
4. Interval Konfidensi Koefisien Regresi
Dengan asumsi bahwa data amatan berdistribusi normal dan independen, interval konfidensi 100(1 − α)% untuk koefisien β dalam regresi linear sederhana adalah:
contoh: Hitung interval konfidensi 95% koefisien pada data sebelumnya.
t½α; n – 2 = t0,025; 8 = 2,306
t½α; n – 2 = t0,025; 8 = 2,306
interval konfidensi untuk β adalah:
panjang sayap = t½α; n – 2.sb = (2,306)(0,02586) = 0,059634
b − 0,059634 ≤ β ≤ b + 0,059634 ↔ 0,31 − 0,059634 ≤ β ≤ 0,31 + 0,059634
0,250366 ≤ β ≤ 0,369634
interval konfidensi untuk α adalah:
panjang sayap = t½α; n – 2.sa = (2,306)(0,034106) = 0,078649
a − 0,078649 ≤ α ≤ a + 0,078649 ↔ 0,24 − 0,078649 ≤ α ≤ 0,24 + 0,078649
0,161351 ≤ α ≤ 0,318649
Jadi, interval konfidensi 95% untuk koefisien konstan adalah 0,161351 ≤ α ≤ 0,318649 dan untuk koefisien regresi adalah 0,250366 ≤ β ≤ 0,369634.


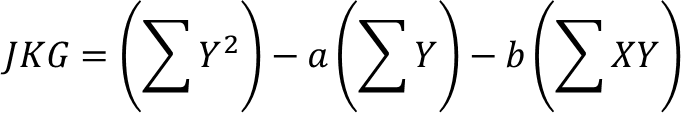
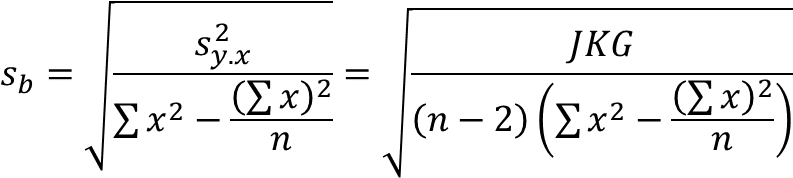





Komentar
Posting Komentar