Integral Fungsi Transenden Khusus
Banyak integral tentu yang tidak dapat diselesaikan dengan menggunakan Teorema Dasar 2 Kalkulus muncul begitu sering dalam matematika terapan sehingga mereka diberi nama khusus. Ada banyak persamaan integral yang rumit dalam matematika yang tidak bisa kita selesaikan dengan cara biasa. Persamaan-persamaan ini sering muncul dalam masalah-masalah nyata, seperti dalam fisika atau teknik. Karena sering digunakan, para ahli matematika memberi nama khusus pada persamaan-persamaan ini. Berikut adalah beberapa fungsi akumulasi ini, bersama dengan nama umum dan singkatannya:
1. Fungsi Galat (Error Function)
3. Integral Sinus Fresnel (Fresnel Sine Integral)
4. Integral Kosinus Fresnel (Fresnel Cosine Integral)
4. Integral Kosinus Fresnel (Fresnel Cosine Integral)
Fungsi-fungsi khusus ini sangat berguna untuk menyelesaikan berbagai masalah. Meskipun terlihat rumit, komputer dapat menghitung nilai perkiraan dari fungsi-fungsi ini dengan sangat cepat dan akurat. Jadi, meskipun kita mungkin tidak bisa menghitungnya dengan tangan, kita tetap bisa memanfaatkannya untuk memecahkan masalah yang lebih besar. Intinya, fungsi khusus adalah persamaan integral yang rumit tapi penting dalam matematika. Meskipun rumit, kita bisa menggunakan komputer untuk menghitungnya.
contoh:
Dalam statistika, terdapat fungsi densitas normal umum, yaitu
P(X ≤ x) = F(x)
P(a ≤ X ≤ b) = P(X ≤ b) − P(X ≤ a) = F(b) − F(a)


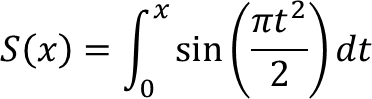
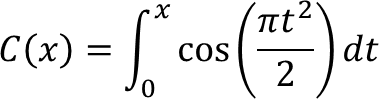
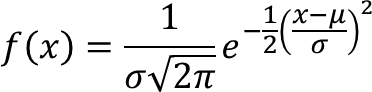
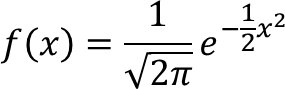







Komentar
Posting Komentar