Deret Tak Hingga
Misal diberikan suatu barisan geometri dengan suku pertama dan rasionya 1/2, barisannya adalah:
1/2, 1/4, 1/8, 1/16, ...
Misal dijumlahkan sebanyak n suku pertama
S1 = 1/2
S2 = 1/2 + 1/4 = 3/4
S3 = 1/2 + 1/4 + 1/8 = 7/8
...
Sn = 1/2 + 1/4 + 1/8 + ... + (1/2)n = 1 − (1/2n)
Apabila jumlah ini dilimitkan menuju tak hingga, akan konvergen ke 1.
Umumnya, deret tak hingga a1 + a2 + a3 + ... dinotasikan:
Definisi: Deret tak hingga a1 + a2 + a3 + ... konvergen dengan jumlah totalnya S jika barisan dari jumlah parsial {Sn} konvergen ke S. Jika {Sn} divergen maka deretnya divergen, dan deret yang divergen tidak memiliki jumlah total.
2. Uji Divergensi Umum
Teorema: Jika suatu deret a1 + a2 + a3 + ... konvergen, maka barisan {an} konvergen ke 0. Kontraposisi dari pernyataan ini adalah jika barisan {an} tidak konvergen ke 0, maka deret a1 + a2 + a3 + ... divergen.
Suatu barisan {an} yang tidak konvergen ke 0 terdapat 2 kemungkinan:
Misal Sn adalah jumlah parsial dari suatu deret, dan {Sn} barisan yang konvergen ke S. Ketahui bahwa rumus umum an = Sn − Sn-1. Karena barisan {Sn} konvergen ke S, tentunya saat n menuju tak hingga, nilainya menuju S, sehingga:
Catatan: Teorema ini tidak berlaku kebalikan. Suatu barisan {an} yang konvergen ke 0, belum tentu {Sn} konvergen.
3. Deret Geometri
Suatu barisan geometri umumnya dinyatakan dengan:
an = arn-1, dengan a ≠ 0, r ≠ 0, r ≠ 1
Jumlah parsial ke-n (yang juga jumlah n suku pertama) adalah:
Sn = a + ar + ar² + ... + arn-1, kalikan masing-masing ruas dengan r − 1
(r − 1)Sn = r(a + ar + ar² + ... + arn-1) − (a + ar + ar² + ... + arn-1) = ar + ar² + ... + arn − (a + ar + ar² + ... + arn-1), tentunya setiap suku akan hilang kecuali:
(r − 1)Sn = a(rn − 1), bagi kembali masing-masing ruas dengan r − 1, diperoleh:
(i) Untuk |r| < 1
Pertimbangkan limit |rn| dengan n menuju ∞. Semakin besar nilai n, semakin |rn| mendekati 0, sehingga rn juga mendekati 0, dan limit n menuju ∞ dari rn adalah 0.
Jadi, untuk |r| < 1, semakin besar nilai n, semakin nilai Sn mendekati a/(1 − r). Dengan kata lain, deret {Sn} konvergen ke a/(1 − r).
(ii) Untuk |r| ≥ 1
Untuk kasus |r| ≥ 1, barisan {an} tidak konvergen ke 0, sehingga deret {Sn} divergen.
4. Deret Harmonik
Misal suatu barisan dinyatakan dengan an = 1/n, barisan ini disebut sebagai barisan harmonik. Ketika kita mengambil limit menuju tak hingga, akan diperoleh:
Dengan kata lain, barisan ini konvergen ke 0.
Akan tetapi, apakah deret yang dibentuk dari barisan ini konvergen?, simak uraian berikut:
Akan tetapi, apakah deret yang dibentuk dari barisan ini konvergen?, simak uraian berikut:
Ternyata deretnya divergen. Kasus ini menunjukkan bahwa teorema uji divergensi umum tidak berlaku kebalikan.
5. Collapsing / Telescoping Series
Barisan t disebut sebagai collapsing / telescoping sequence jika dapat dinyatakan dalam:
tn = an+1 − an, yaitu selisih dari dua suku berurutan dari suatu barisan (an).
Sebagai konsekuensinya, jumlah parsial hanya terdiri dari selisih dua suku dari {an}, setelah dilakukan kanselasi (penyingkatan). Teknik penyingkatan ini, di mana sebagian dari setiap suku saling menyingkat dengan sebagian dari suku berikutnya, dikenal sebagai metode selisih.
Bayangkan sebuah teleskop yang ditarik. Ketika ditarik, bagian-bagian teleskop akan saling menyusut masuk ke bagian lainnya. Deret teleskopik bekerja dengan prinsip yang mirip. Setiap suku dalam deret ini memiliki bagian yang saling menghilangkan dengan suku berikutnya, sehingga ketika kita menjumlahkan suku-suku tersebut, sebagian besar suku akan saling menghilangkan, menyisakan hanya sedikit suku yang tidak terhapus.
Jumlah parsial ke-n dari deret teleskopik adalah:
Biasanya deret teleskopik digunakan pada fungsi rasional dalam bentuk fraksi parsial (jika memungkinkan).
contoh:
contoh:
Diberikan tn = 12/(n² + 5n + 4) untuk n ≥ 1, apakah membentuk deret konvergen?
Buat dekomposisi fraksi parsial:
Bentuk ini memungkinkan untuk menggunakan deret teleskopik karena memungkinkan kanselasi. Berikut rumus jumlah parsial terkanselasi:
6. Linearitas Deret Konvergen
Misal dua barisan {an} dan {bn} masing-masing membentuk deret yang konvergen, dan c konstanta, berlaku linearitas:
(i) Perkalian Skalar
Jika barisan {an} membentuk deret yang divergen dan c ≠ 0, maka hasil perkalian skalar membentuk deret yang divergen.
Terkadang kita lupa akan definisi deret tak hingga sebagai limit dari barisan jumlah parsial, dan kita membiarkan intuisi kita membawa kita pada paradoks. Sebagai contoh, deret
1 − 1 + 1 − 1 + ... + (−1)n+1 + ...
memiliki jumlah parsial
S₁ = 1
S₂ = 1 − 1 = 0
S₃ = 1 − 1 + 1 = 1
S₄ = 1 − 1 + 1 − 1 = 0
...
Barisan jumlah parsial, 1, 0, 1, 0, 1, ..., divergen; sehingga deret 1 − 1 + 1 − 1 + ... juga divergen. Namun, kita mungkin melihat deret ini sebagai
(1 − 1) + (1 − 1) + (1 − 1) + ...
dan mengklaim bahwa jumlahnya adalah 0. Atau, kita mungkin melihat deret ini sebagai
1 − (1 − 1) − (1 − 1) − (1 − 1) − ...
dan mengklaim bahwa jumlahnya adalah 1. Lebih aneh lagi, kita menggunakan bentuk rekursif:
S = 1 − (1 − 1 + 1 − 1 + ...) = 1 − S
2S = 1
S = ½
Jumlah dari deret ini tidak mungkin sama dengan 0, 1, dan ½ sekaligus.
Paradoks ini terjadi karena kita mencoba menerapkan operasi aljabar biasa pada deret tak hingga, padahal tidak semua sifat aljabar yang berlaku untuk jumlah hingga juga berlaku untuk jumlah tak hingga. Pengelompokan suku-suku dalam deret tak hingga dapat mengubah hasil penjumlahan, terutama untuk deret yang tidak konvergen.
Deret 1 − 1 + 1 − 1 + ... adalah contoh dari deret yang tidak konvergen. Kita tidak bisa memberikan nilai yang pasti untuk jumlah deret ini karena hasil penjumlahannya akan tergantung pada cara kita mengelompokkan suku-sukunya. Oleh karena itu, dalam mempelajari deret tak hingga, kita harus sangat berhati-hati dan tidak menggeneralisasi sifat-sifat dari jumlah hingga ke jumlah tak hingga.
9. Pengelompokan Suku
Suku-suku dari deret konvergen dapat dikelompokkan dengan cara apa pun (asalkan urutan suku-suku dipertahankan), dan deret baru yang terbentuk akan konvergen dengan jumlah yang sama dengan deret aslinya.
Kita bisa mengelompokkan suku-suku dalam deret konvergen dengan cara apa pun yang kita inginkan, asalkan urutannya tidak berubah. Meskipun kita mengelompokkan suku-suku, jumlah total dari deret tersebut akan tetap sama. Dengan mengelompokkan suku-suku dengan cara yang tepat, kita bisa menyederhanakan perhitungan dan menemukan jumlah deret dengan lebih mudah.
Sifat pengelompokan suku dalam deret konvergen adalah salah satu sifat yang membedakan deret konvergen dengan deret divergen. Deret divergen tidak memiliki sifat ini, artinya cara kita mengelompokkan suku-suku dalam deret divergen dapat mengubah hasil penjumlahannya.

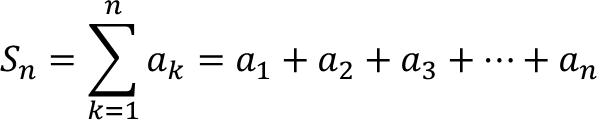







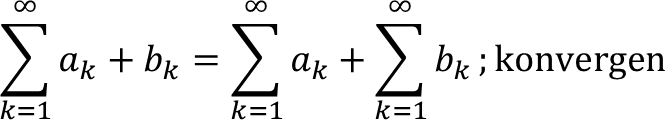


Komentar
Posting Komentar