Fungsi Dua Variabel

1. Fungsi Dua Variabel

Fungsi dua variabel f mengaitkan setiap pasangan terurut (x, y) yang merupakan anggota himpunan D pada bidang dengan tepat satu bilangan real f(x, y). Himpunan D disebut daerah asal fungsi. Jika tidak dinyatakan secara spesifik, kita menganggap D adalah daerah asal alamiah, yaitu himpunan terbesar di mana fungsi terdefinisi. Daerah hasil fungsi adalah himpunan dari semua nilai fungsi. Dengan cara yang sama, kita dapat mengembangkan fungsi tiga atau lebih variabel riil.

contoh:

Tentukan domain dari fungsi

Agar nilai fungsi terdefinisi, diharuskan keduanya terdefinisi.

Apabila digambarkan, grafik domainnya adalah:

2. Grafik Fungsi Dua Variabel

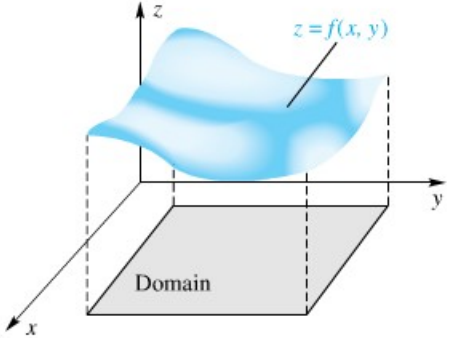
Jika f fungsi dua variabel dengan daerah asal D, grafik dari f adalah himpunan semua titik (x, y, z) di ruang demikian sehingga z = f(x, y) dan (x, y) ∈ D.

contoh:

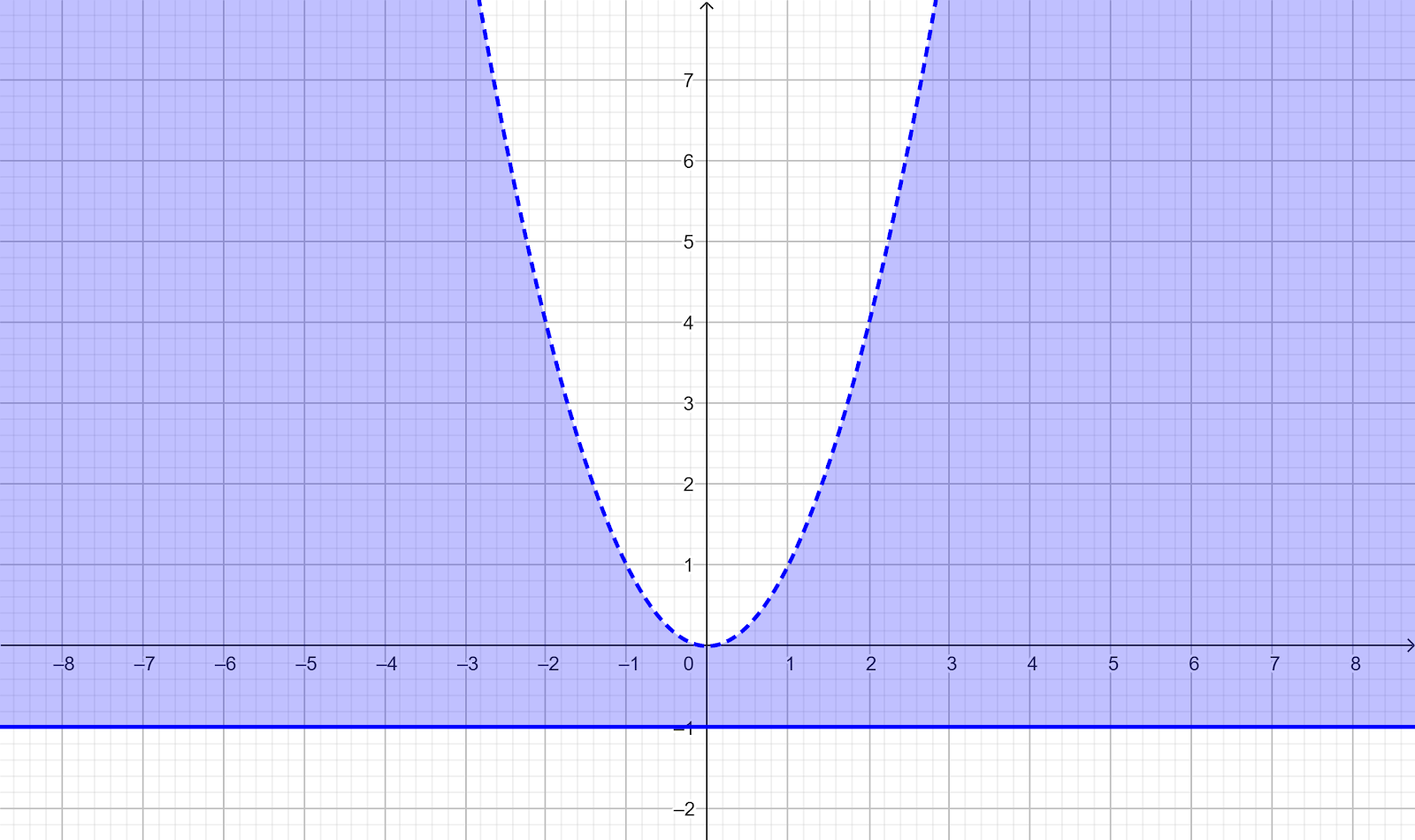
Buatlah grafik fungsi f(x, y) = sqrt(y + 1) + ln(x² − y)

3. Kurva Ketinggian dan Peta Kontur

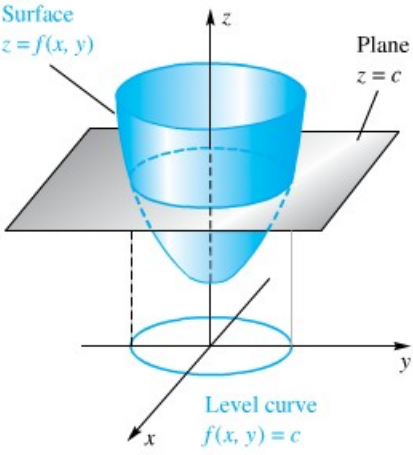
Jika irisan bidang z = k dengan permukaan z = f(x, y) diproyeksikan pada bidang XOY diperoleh suatu kurva yang disebut sebagai kurva ketinggian yang bersesuaian dengan ketinggian k. Persamaan kurva ketinggian tersebut adalah f(x, y) = k.

Sedangkan kumpulan dari kurva ketinggian disebut sebagai Peta Kontur.

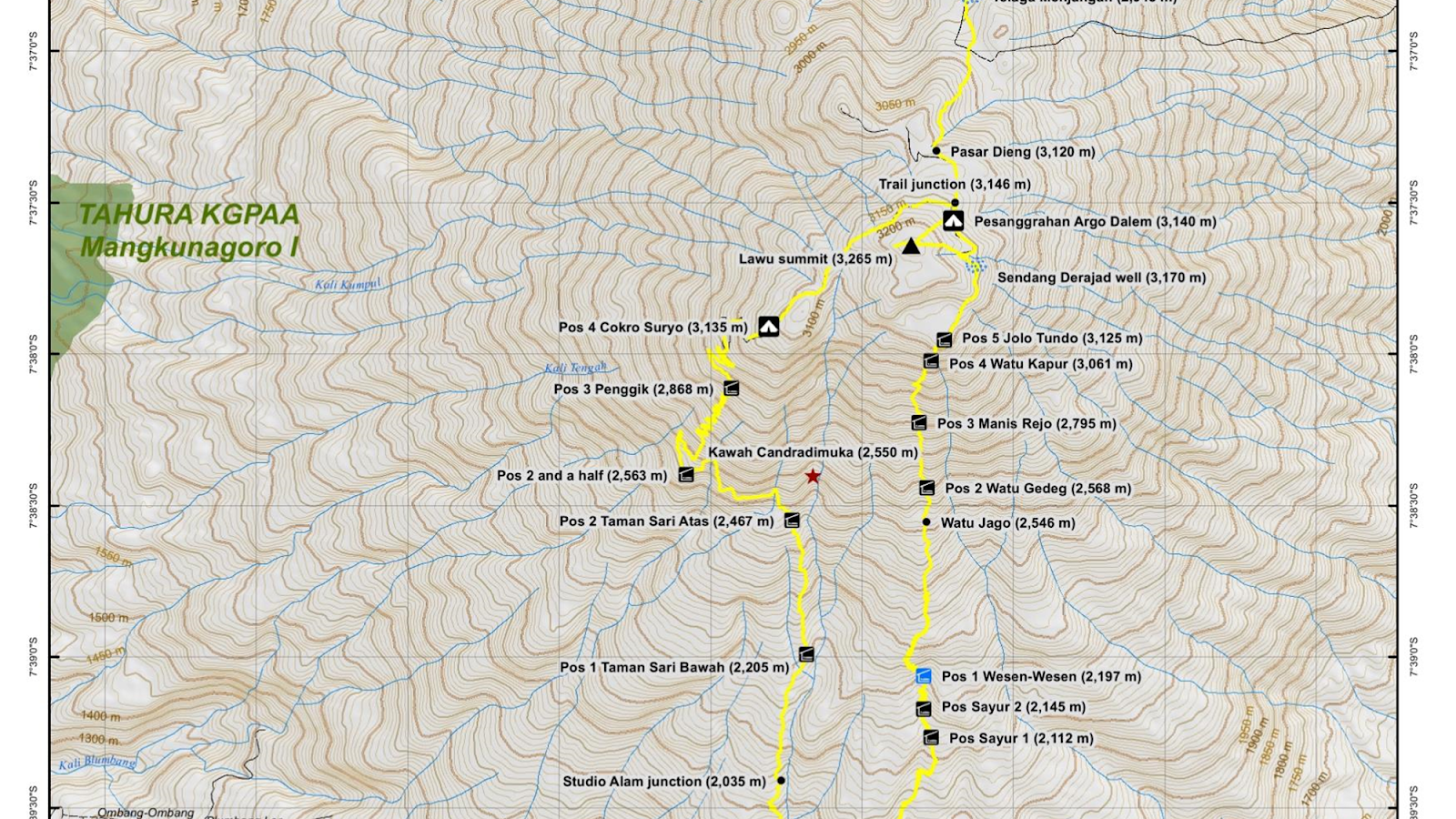
Bayangkan memotong sebuah gunung dengan bidang horisontal. Setiap potongan akan menghasilkan garis kontur. Garis-garis kontur ini digambar pada peta untuk menunjukkan bentuk dan ketinggian gunung. Peta kontur membuat kita lebih mudah memahami bentuk permukaan yang kompleks, seperti permukaan gunung, lembah, atau bahkan grafik fungsi matematika. Bayangkan Anda melihat peta topografi. Garis-garis pada peta itu adalah kurva tingkat. Garis yang rapat menunjukkan area yang curam, sedangkan garis yang jarang menunjukkan area yang datar. Kurva tingkat adalah alat yang sangat berguna dalam visualisasi data tiga dimensi. Dengan memahami konsep ini, Anda dapat lebih mudah menginterpretasikan grafik fungsi dua variabel dan peta topografi.

Contoh 1: Buatlah peta kontur dari fungsi f(x, y) = x − ⅑x³ – ½y²

(i) Buat grafik fungsi, potongkan dengan bidang-bidang yang sejajar XOY

(ii) Proyeksikan potongan-potongan tersebut ke bidang XOY

Contoh 2: Peta Kontur Gunung Lawu

Contoh 3: Peta kontur dari fungsi f(x, y) = ln(x² + y² − 1)

4. Penerapan Peta Kontur

Peta kontur sering digunakan untuk menunjukkan cuaca atau kondisi lain di berbagai titik pada peta. Misalnya, suhu bervariasi dari satu tempat ke tempat lain. Kita dapat membayangkan T(x, y) sebagai suhu di lokasi (x, y). Kurva tingkat untuk suhu yang sama disebut isoterm atau kurva isotermal. Sebagai contoh, gambar berikut menunjukkan peta isoterm untuk Amerika Serikat:

Pada tanggal 9 April 1917, gempa bumi kuat berpusat di dekat Sungai Mississippi, tepat di selatan St. Louis, terasa hingga sejauh utara Iowa dan sejauh selatan Mississippi. Intensitas gempa bumi diukur dari I hingga XII, dengan angka yang lebih tinggi sesuai dengan gempa bumi yang lebih parah. Gempa bumi berkekuatan VI akan menyebabkan kerusakan fisik pada bangunan.

Jika kita membayangkan intensitas I sebagai fungsi dari lokasi (x, y), maka kita dapat menggambarkan intensitas gempa bumi menggunakan peta dengan kurva tingkat yang sesuai dengan intensitas yang sama. Kurva dengan intensitas konstan disebut kurva isoseismik. Sebagai contoh, gambar berikut menunjukkan bahwa wilayah yang mengalami intensitas VI meliputi wilayah St. Louis dan sebuah jalur di tenggara Missouri:

Sebagian besar Missouri timur dan Illinois barat daya mengalami intensitas antara V dan VI. Karena Kansas City dan Memphis berada di dekat kurva isoseismik yang sama, intensitasnya kira-kira sama di Kansas City dan Memphis.

Pada intinya, peta kontur sangat berguna untuk memvisualisasikan data spasial dan memahami distribusi fenomena seperti suhu, curah hujan, atau intensitas gempa bumi. Dengan melihat peta kontur, kita dapat dengan mudah mengidentifikasi daerah dengan nilai tinggi atau rendah, serta pola-pola spasial lainnya.

5. Fungsi Dengan Tiga atau Lebih Variabel

Banyak besaran bergantung pada tiga variabel atau lebih. Misalnya, suhu di sebuah auditorium besar dapat bergantung pada lokasi (x, y, z); ini mengarah pada fungsi T(x, y, z). Kecepatan aliran fluida dapat bergantung pada lokasi (x, y, z), serta waktu t; ini mengarah pada fungsi V(x, y, z, t). Terakhir, nilai rata-rata ujian di kelas dengan 50 siswa bergantung pada 50 nilai ujian x₁, x₂, ..., x₅₀; ini mengarah pada fungsi A(x₁, x₂, ..., x₅₀).

Kita dapat memvisualisasikan fungsi dengan tiga variabel dengan membuat plot permukaan tingkat, yaitu permukaan dalam ruang tiga dimensi yang menghasilkan nilai konstan untuk fungsi tersebut. Fungsi dengan empat variabel atau lebih jauh lebih sulit untuk divisualisasikan. Daerah asal alami dari fungsi dengan tiga variabel atau lebih adalah himpunan semua pasangan terurut (atau rangkap empat, dan seterusnya) yang masuk akal untuk fungsi tersebut dan menghasilkan bilangan real.

Fungsi tidak selalu hanya bergantung pada satu atau dua variabel. Ada banyak situasi di mana nilai suatu besaran dipengaruhi oleh lebih banyak variabel. Untuk fungsi dengan tiga variabel, kita bisa membayangkan permukaan 3D. Setiap titik pada permukaan mewakili nilai fungsi untuk kombinasi tertentu dari ketiga variabel. Daerah asal adalah semua kemungkinan nilai yang bisa dimasukkan ke dalam fungsi.

Pada intinya, konsep fungsi tidak terbatas pada dua variabel. Dalam banyak situasi nyata, kita perlu mempertimbangkan lebih banyak variabel untuk mendapatkan gambaran yang lebih lengkap.