Turunan Parsial

1. Turunan Parsial

Misalkan f adalah fungsi dari dua variabel x dan y. Jika salahsatu variabel dibuat konstan, maka f menjadi fungsi satu variabel.

a. Turunan parsial f(x, y) terhadap x, berarti variabel y pada f(x, y) dianggap konstan, dinyatakan dengan f_x(x, y), dan didefinisikan sebagai:

b. Turunan parsial f(x, y) terhadap y, berarti variabel x pada f(x, y) dianggap konstan, dinyatakan dengan f_y(x, y), dan didefinisikan sebagai:

Simbol yang digunakan untuk menyatakan turunan parsial adalah 𝜕. Misal z = f(x, y), kita dapat menyatakan f_x(x, y) dengan 𝜕z/𝜕x, juga f_y(x, y) dengan 𝜕z/𝜕y.

Konsep ini menjelaskan bagaimana kita bisa melihat sebuah fungsi dari dua variabel sebagai fungsi dari satu variabel saja jika salah satu variabelnya dianggap konstan. Misalnya, jika kita memiliki fungsi yang menggambarkan suhu di suatu ruangan (yang bergantung pada panjang dan lebar ruangan), kita bisa memikirkan bagaimana suhu berubah jika kita hanya mengubah panjang ruangan sambil menjaga lebarnya tetap.

Penggunaan aturan dan rumus-rumus turunan yang ada pada turunan fungsi satu variabel (turunan biasa) untuk turunan parsial ke x, variabel y dianggap konstanta dan sebaliknya untuk turunan parsial ke y variabel x dianggap konstanta, kemudian mengganti nilai x dan y dengan nilai yang diminta.

contoh:

1. Diberikan f(x, y) = x²y + 3y³, tentukan f_x(1, 2) dan f_y(1, 2)

f_x(x, y) = 2xy; f_x(1, 2) = 2.1.2 = 4

f_y(x, y) = x² + 9y²; f_y(1, 2) = 1² + 9.2² = 37

2. Tentukan turunan parsial terhadap x maupun y dari fungsi f(x, y) = x⁴.sin(xy³)

f_x(x, y) = 4x³.sin(xy³) + x⁴.cos(xy³).y³

f_y(x, y) = x⁴.cos(xy³).3xy²

2. Interpretasi Geometri Turunan Parsial

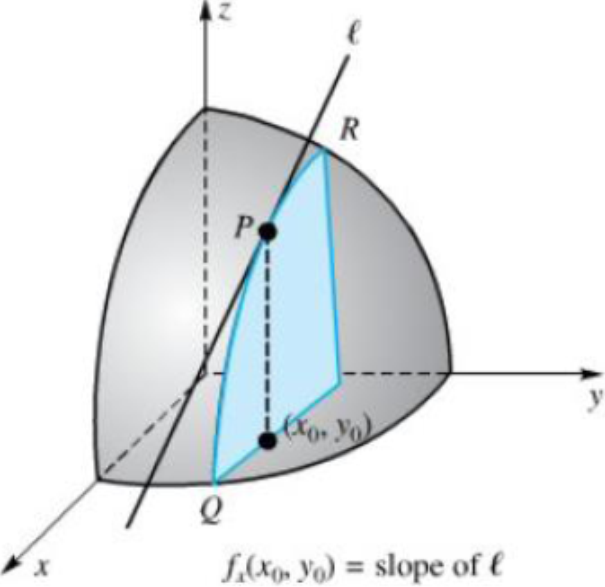
Pertimbangkan permukaan yang persamaannya adalah z = f(x, y). Bidang y = y₀ memotong permukaan ini dalam kurva bidang, dan nilai f_x(x₀, y₀) adalah kemiringan garis singgung pada kurva ini di titik P(x₀, y₀, f(x₀, y₀)). Demikian pula, bidang x = x₀ memotong permukaan dalam kurva bidang, dan f_y(x₀, y₀) adalah kemiringan garis singgung pada kurva ini di titik P.

Turunan parsial juga dapat diartikan sebagai laju perubahan (sesaat) suatu besaran. Misalkan ada sebuah senar biola yang ujungnya terikat di titik A dan B, dan senar tersebut bergetar pada bidang xz. Posisi senar pada suatu waktu tertentu t. Jika z = f(x, t) menyatakan tinggi senar pada titik P dengan koordinat x pada waktu t, maka ∂z/∂x adalah kemiringan senar di titik P, dan ∂z/∂t adalah laju perubahan tinggi titik P terhadap waktu sepanjang garis vertikal yang ditunjukkan. Dengan kata lain, ∂z/∂t adalah kecepatan vertikal titik P.

contoh:

Tentukan persamaan parameter garis singgung kurva perpotongan z = f(x, y) = x² + y² dengan bidang x = 1 di titik (1, 2, 5)

f_y(x, y) = 2y; f_y(1, 2) = 4. Inilah kemiringan garis singgung kurva di titik (1, 2, 5) dalam arah sumbu y. Artinya, jika kita bergerak sedikit ke arah y dari titik tersebut, nilai z akan naik dengan laju 4.

Dari kemiringan yang kita dapatkan, kita bisa menentukan vektor arah garis singgung. Vektor arah ini adalah ⟨0, 1, 4⟩. Komponen x adalah 0 karena x konstan (x = 1), komponen y adalah 1 karena kita bergerak searah sumbu y, dan komponen z adalah 4 sesuai dengan kemiringan yang kita hitung.

Kita sudah memiliki titik yang dilalui garis singgung (1, 2, 5) dan vektor arahnya. Dengan menggunakan persamaan parametrik garis, kita dapat menulis persamaan garis singgung sebagai berikut:

(x, y, z) = (1, 2, 5) + t(0, 1, 4)

x = 1,    y = 2 + t,    z = 5 + 4t

3. Turunan Parsial Tingkat Tinggi

Karena turunan parsial dari suatu fungsi terhadap x dan y, pada umumnya, merupakan fungsi lain dari dua variabel yang sama, maka fungsi ini dapat diturunkan parsial lagi terhadap x atau y, menghasilkan empat turunan parsial tingkat dua dari f.

Meskipun simbol turunan bukan merupakan pecahan, tetapi turunan parsial tingkat tinggi seolah-olah memiliki sifat komutatif pada mayoritas kasus, yaitu f_xy(x, y) = f_yx(x, y), secara simbol terlihat membenarkannya, meskipun kesamaan ini salah pada minoritas kasus, hal ini akan dimengerti setelah mempelajari limit dan kontinuitas fungsi dua atau lebih variabel.

contoh:

1. Tentukan keempat turunan parsial tingkat dua dari f(x, y) = sin(x/y) + x³y²

Turunan tingkat satu:

Turunan tingkat dua:

Kasus ini termasuk kasus mayoritas, dimana f_xy(x, y) = f_yx(x, y) merupakan kesamaan yang benar.

2. Volume suatu gas tertentu dihubungkan terhadap suhunya 𝑇 dan tekanannya 𝑃 menurut hukum gas 𝑃𝑉 = 10𝑇, dengan 𝑉 diukur dalam meter kubik, 𝑃 dalam kg per meter persegi, dan 𝑇 dalam Kelvin. Jika 𝑉 dijaga tetap konstan pada 50, berapakah laju perubahan tekanan terhadap suhu ketika 𝑇 = 200?

𝑃𝑉 = 10𝑇 berarti P = 10T/V, sehingga ∂P/∂T = 10/V

Karena nilai V dijaga konstan pada 50, pada saat T = 200, ∂P/∂T = 10/V = 10/50 = 0,2

Jadi, tekanan bertambah besar pada laju 0,2 kg per meter kubik per Kelvin.

Lanjutan: Turunan parsial tingkat tiga dan lebih tinggi didefinisikan dengan cara yang serupa, dan notasinya juga mirip. Jadi, jika f adalah fungsi dari dua variabel x dan y, maka turunan parsial tingkat tiga dari f yang diperoleh dengan mendiferensialkan f secara parsial, pertama terhadap x dan kemudian dua kali terhadap y, akan dinotasikan dengan:

4. Turunan Parsial Fungsi Lebih dari Dua Variabel

Misalkan f adalah fungsi dari tiga variabel, x, y, dan z. Turunan parsial dari f terhadap x pada titik (x, y, z) dinotasikan dengan f_x(x, y, z) atau ∂f(x, y, z)/∂x dan didefinisikan sebagai:

Dengan demikian, f_x(x, y, z) dapat diperoleh dengan menganggap y dan z sebagai konstanta dan mendiferensiasikan terhadap x.

Turunan parsial terhadap y dan z didefinisikan dengan cara yang serupa. Turunan parsial dari fungsi dengan empat variabel atau lebih didefinisikan dengan cara yang sama. Turunan parsial seperti f_xy dan f_xyz yang melibatkan diferensiasi terhadap lebih dari satu variabel disebut turunan parsial campuran.