Aturan Rantai, Fungsi Implisit, Bidang Singgung (KPB)

Ingat kembali aturan rantai pada fungsi satu variabel. Misal y = f(x(t)), dengan f dan x keduanya dapat diturunkan, kita dapat menentukan turunan y terhadap t dengan:

Lalu bagaimana untuk fungsi lebih dari satu variabel? Apakah analog umum dari aturan rantai satu variabel berlaku? Ya, dan berikut adalah pernyataan yang sangat elegan tentang hal itu. Misalkan R menyatakan bilangan real dan Rⁿ menyatakan ruang Euclidean n-dimensi, misalkan g adalah fungsi dari R ke Rⁿ, dan misalkan f adalah fungsi dari Rⁿ ke R. Jika g dapat diturunkan pada t dan jika f dapat diturunkan pada g(t), maka fungsi komposit f ∘ g dapat diturunkan pada t dan

(f ∘ g)'(t) = ∇f(g(t)) · g'(t)

1. Aturan Rantai Versi I

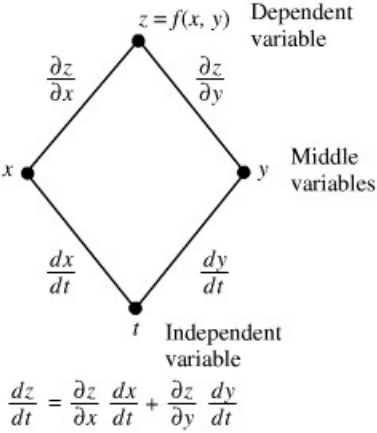
Misal x = x(t) dan y = y(t) terdiferensialkan di t, dan misal z = f(x, y) terdiferensialkan di (x(t), y(t)), maka z = f(x(t), y(t)) terdiferensialkan di t dengan:

atau misalkan p = (x, y) kita dapat menyatakannya:

Contoh 1: Kasus untuk dua variabel

Ketika sebuah tabung lingkaran tegak dipanaskan, jari-jarinya (𝑟) dan tingginya (ℎ) bertambah, sehingga otomatis permukaannya (𝑆) juga bertambah luas. Misalkan pada saat 𝑟 = 10 𝑐𝑚 dan ℎ = 100 𝑐𝑚, 𝑟 bertambah pada laju 0,2 𝑐𝑚/𝑗𝑎𝑚 dan ℎ bertambah pada laju 0,5 𝑐𝑚/𝑗𝑎𝑚. Berapakah laju pertamabahan luas 𝑆 pada saat tersebut?

Rumus total seluruh permukaan sebuah tabung adalah 𝑆 = 2𝜋𝑟ℎ + 2𝜋𝑟²

Sehingga laju pertambahan 𝑆 diperoleh sebagai berikut:

= 2𝜋ℎ + 4𝜋𝑟 (0,2) + 2𝜋ℎ (0,5)

Laju pertambahan 𝑆 pada saat 𝑟 = 10 𝑐𝑚 dan ℎ = 100 𝑐𝑚 adalah

2𝜋.100 + 4𝜋.10.(0,2) + 2𝜋.10.(0,5) = 58𝜋 𝑐𝑚²/jam.

Jadi, laju pertamabahan luas 𝑆 pada saat tersebut adalah 58𝜋 𝑐𝑚²/jam.

Contoh 2: Kasus untuk tiga variabel

Misal w = x²y + y + xz, dimana x = cos(θ), y = sin(θ), z = θ², tentukan dw/dθ.

dw/dθ = (2xy + z)(−sin(θ)) + (x² + 1)cos(θ) + x.2θ

= −2cos(θ)sin²(θ) − θ².sin(θ) + cos³(θ) + cos(θ) + 2θ.cos(θ)

2. Aturan Rantai Versi II

Misal x = x(s, t) dan y = y(s, t) terdiferensialkan di (s, t) dan misal z = f(x, y) terdiferensialkan di (x(s, t), y(s, t)), maka z = f(x(s, t), y(s, t)) terdiferensialkan parsial di (s, t) dengan

Contoh:

Misal z = 3x² − y², dimana x = 2s + 7t dan y = 5st, tentukan 𝜕z/𝜕t dalam s dan t!

Gunakan aturan rantai versi II

𝜕z/𝜕t = 6x.7 + (−2y).5s = 42(2s + 7t) −10st.5s = 84s + 294t − 50s²t

3. Fungsi Implisit

Anggaplah persamaan F(x, y) = 0 secara implisit mendefinisikan y sebagai fungsi dari x, misalnya y = g(x), tetapi fungsi g sulit atau bahkan tidak mungkin untuk ditentukan secara eksplisit. Kita tetap dapat mencari turunan dy/dx. Salah satu metode untuk melakukannya, yaitu diferensiasi implisit. Berikut ini adalah metode lain untuk menentukannya.

Mari kita diferensialkan kedua sisi persamaan F(x, y) = 0 terhadap x dengan menggunakan aturan rantai. Kita akan mendapatkan:

Dengan menyelesaikan persamaan di atas untuk dy/dx, kita memperoleh rumus:

Jika z merupakan fungsi implisit dari x dan y yang didefinisikan oleh persamaan F(x, y, z) = 0, maka dengan mendiferensialkan kedua sisi persamaan terhadap x sambil menganggap y sebagai konstanta, kita akan mendapatkan:

Jika kita menyelesaikan persamaan di atas untuk dz/dx dan mengingat bahwa dy/dx = 0 (karena y dianggap konstanta), kita akan mendapatkan rumus pertama berikut ini. Dengan cara yang serupa, jika kita menganggap x sebagai konstanta dan mendiferensialkan terhadap y, kita akan mendapatkan rumus kedua.

Contoh:

Misal F(x, y, z) = x³e^y+z − y.sin(x − z) = 0 mendefinisikan secara implisit z sebagai fungsi dari x dan y, tentukan turunan parsial z terhadap x.

4. Bidang Singgung

Ingat kembali persamaan bidang singgung permukaan z = f(x, y) di titik (x₀, y₀, f(x₀, y₀)) adalah

z = f(x₀, y₀) + ∇f(x₀, y₀) · 〈x − x₀, y − y₀〉

Telah diperkenalkan konsep bidang singgung suatu permukaan, namun hanya untuk permukaan yang ditentukan oleh persamaan bentuk z = f(x, y). Sekarang, kita ingin mempertimbangkan situasi yang lebih umum, yaitu permukaan yang ditentukan oleh F(x, y, z) = k. (Perhatikan bahwa z = f(x, y) dapat ditulis sebagai F(x, y, z) = f(x, y) − z = 0). Pertimbangkan sebuah kurva pada permukaan ini yang melalui titik (x₀, y₀, z₀). Jika x = x(t), y = y(t), dan z = z(t) adalah persamaan parametrik untuk kurva ini, maka untuk setiap t,

F(x(t), y(t), z(t)) = k

Dengan menggunakan aturan rantai, kita dapatkan:

Kita dapat mengekspresikan ini dalam bentuk gradien dari F dan turunan dari vektor posisi kurva r(t) = x(t)i + y(t)j + z(t)k sebagai:

Sebagaimana telah dibahas bahwa dr/dt adalah garis singgung kurva. Oleh karena itu, gradien ∇𝐹 di (x₀, y₀, z₀) tegak lurus dengan garis singgung kurva di titik ini.

Ketegaklurusan ini berlaku untuk setiap kurva yang melalui (x₀, y₀, z₀) di permukaan F(x, y, z) = k. 

Garis singgung dari kurva-kurva pada permukaan yang berpotongan suatu titik akan membentuk bidang singgung di titik tersebut. Gradien di titik (x₀, y₀, z₀) tegak lurus bidang singgung yang melalui titik tersebut.

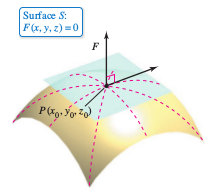
Misalkan F(x, y, z) = k mendefinisikan sebuah permukaan, dan misalkan F terdiferensialkan pada titik P(x₀, y₀, z₀) dari permukaan ini, dengan ∇F(x₀, y₀, z₀) ≠ 0. Maka, bidang yang melalui titik P dan tegak lurus terhadap ∇F(x₀, y₀, z₀) disebut bidang singgung permukaan F(x, y, z) = k di titik P.

5. Rumus Bidang Singgung

Untuk permukaan F(x, y, z) = k, persamaan bidang singgung di titik P(x₀, y₀, z₀) adalah:

∇F(x₀, y₀, z₀) · 〈x − x₀, y − y₀, z − z₀〉 = 0

atau dengan kata lain,

F_x(x₀, y₀, z₀)(x − x₀) + F_y(x₀, y₀, z₀)(y − y₀) + F_z(x₀, y₀, z₀)(z − z₀) = 0

Secara khusus, untuk permukaan z = f(x, y), persamaan bidang singgung pada titik (x₀, y₀, f(x₀, y₀)) adalah:

z − z₀ = f_x(x₀, y₀)(x − x₀) + f_y(x₀, y₀)(y − y₀)

Contoh:

Tentukan persamaan bidang singgung dan garis normal permukaan x² + y² + 2z² = 23 di titik (1, 2, 3).

Misal F(x, y, z) = x² + y² + 2z² − 23, gradien ∇F(x, y, z) adalah 2xi + 2yj + 4zk, sehingga

∇F(1, 2, 3) = 2i + 4j + 12k.

Persamaan bidang singgung di (1, 2, 3) adalah 2(x − 1) + 4(y − 2) + 12(z − 3) = 0

Bisa juga dituliskan x + 2y + 6z − 23 = 0

Sedangkan persamaan garis normal di (1, 2, 3) adalah