Turunan Berarah dan Gradien
Ingat kembali suatu fungsi f(x, y) dari dua variabel. Turunan parsial fx(x, y) dan fy(x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah yang sejajar dengan sumbu x dan y. Tujuan kita sekarang adalah mempelajari laju perubahan f pada arah sembarang. Hal ini mengarah pada konsep turunan berarah, yang pada gilirannya terkait dengan gradien.
Akan lebih mudah jika kita menggunakan notasi vektor. Misalkan p = (x, y), dan i dan j adalah vektor satuan pada arah positif sumbu x dan y. Maka, kedua turunan parsial di titik p dapat ditulis sebagai berikut:
Untuk mendapatkan konsep yang kita cari, yang perlu kita lakukan adalah mengganti i atau j dengan vektor satuan sembarang u. Dengan mengganti i atau j dengan vektor satuan sembarang u, kita dapat menghitung laju perubahan fungsi f pada arah yang ditentukan oleh vektor u. Ini adalah dasar dari konsep turunan arah.
1. Definisi dan Interpretasi Geometri Turunan Berarah
Untuk setiap vektor satuan u, misal
Dengan demikian, turunan arah dari f pada titik p dalam arah i adalah fx(p) dan dalam arah j adalah fy(p). Karena p = (x, y), kita juga menggunakan notasi Duf(x, y). Vektor u menentukan sebuah garis L pada bidang xy yang melalui (x₀, y₀).
Bidang yang melalui L dan tegak lurus terhadap bidang XOY memotong permukaan z = f(x, y) pada sebuah kurva C. Garis singgung pada kurva C di titik (x₀, y₀, f(x₀, y₀)) memiliki kemiringan Duf(x₀, y₀). Interpretasi lain yang berguna adalah bahwa Duf(x₀, y₀) mengukur laju perubahan f terhadap jarak dalam arah u.
Dengan kata lain, nilai Duf(x₀, y₀) adalah kemiringan garis singgung kurva perpotongan permukaan z = f(x, y) dengan bidang sejajar u tegak lurus bidang XOY di titik P(x₀, y₀, f(x₀, y₀)). Duf(x₀, y₀) adalah kemiringan garis singgung di P.
2. Hubungan dengan Gradien
Ingat kembali bahwa ∇f(p) = fx(p)i + fy(p)j.
Misalkan f dapat diturunkan di titik p. Maka f memiliki turunan arah di p dalam arah vektor satuan u = u1i + u2j dan
Duf(p) = u · ∇f(p)
Artinya,
Duf(x, y) = u1fx(x, y) + u2fy(x, y)
Contoh:
Diberikan f(x, y) = 4x² − xy + 3y², tentukan turunan berarah f di titik (2, −1) pada arah vektor a = 4i + 3j.
Vektor satuan u dengan arah a adalah ⅘i + ⅗j.
fx(x, y) = 8x − y dan fy(x, y) = −x + 6y
fx(2, −1) = 17 dan fy(2, −1) = −8
Duf(2, −1) = 〈⅘, ⅗〉 · 〈17, −8〉 = ⅘(17) + ⅗(−8) = 44/5
3. Laju Perubahan Maksimum
Untuk suatu fungsi f pada titik tertentu p, adalah wajar untuk bertanya ke arah mana fungsi tersebut berubah paling cepat, yaitu, ke arah mana Duf(p) memiliki nilai terbesar? Dari rumus geometri untuk perkalian titik, kita dapat menulis
Duf(p) = u · ∇f(p) = ‖u‖ ‖∇f(p)‖ cos(θ) = ‖∇f(p)‖ cos(θ)
di mana θ adalah sudut antara u dan ∇f(p). Dengan demikian, Duf(p) mencapai nilai maksimum ketika θ = 0 dan nilai minimum ketika θ = π. Kita dapat merangkum sebagai berikut.
Suatu fungsi meningkat paling cepat pada titik p dalam arah gradien (dengan laju ‖∇f(p)‖) dan menurun paling cepat pada arah yang berlawanan (dengan laju −‖∇f(p)‖).
Bayangkan sebuah permukaan bukit. Gradien pada suatu titik pada permukaan bukit akan menunjuk ke arah kemiringan yang paling curam. Jika Sixtyfourians berjalan searah dengan gradien, Anda akan naik dengan paling cepat. Sebaliknya, jika Anda berjalan berlawanan arah dengan gradien, Anda akan turun dengan paling cepat.
4. Kurva Ketinggian dan Gradiennya
Ingat kembali bahwa kurva ketinggian dari permukaan z = f(x, y) adalah proyeksi ke bidang XOY dari kurva perpotongan antara permukaan dengan bidang z = k yang sejajar dengan bidang XOY. Nilai fungsi pada semua titik pada kurva ketinggian yang sama adalah konstan.
Misalkan L adalah kurva ketinggian dari f(x, y) yang melalui titik sembarang P(x₀, y₀) di domain f, dan misalkan vektor satuan u adalah vektor singgung satuan terhadap L di P. Karena nilai f sama pada semua titik pada kurva ketinggian L, turunan arahnya Duf(x₀, y₀), yang merupakan laju perubahan f(x, y) dalam arah u, adalah nol ketika u adalah vektor singgung satuan terhadap L.
Karena
0 = Duf(x₀, y₀) = ∇f(x₀, y₀) · u
kita menyimpulkan bahwa ∇f(x₀, y₀) dan u tegak lurus.
Bayangkan sebuah peta topografi. Garis-garis kontur pada peta tersebut adalah kurva tingkat yang menunjukkan ketinggian yang sama. Gradien pada suatu titik akan menunjuk ke arah kemiringan yang paling curam. Jika Anda berjalan sepanjang garis kontur, ketinggian Anda tidak akan berubah karena Anda bergerak tegak lurus terhadap arah kemiringan.
Gradien dari f pada titik P tegak lurus terhadap kurva ketinggian dari f yang melalui P.
Bayangkan sebuah bukit. Garis kontur pada peta bukit adalah kurva tingkat. Jika Anda berdiri di suatu titik pada bukit, gradien pada titik itu akan menunjuk ke arah yang paling curam, yaitu tegak lurus terhadap garis kontur yang melewati titik tersebut.
Peta cuaca: Garis isobar (garis yang menghubungkan titik-titik dengan tekanan udara yang sama) adalah kurva ketinggian. Gradien tekanan udara pada suatu titik akan tegak lurus terhadap garis isobar, menunjukkan arah angin.
Permukaan air: Garis kontur pada peta kedalaman laut adalah kurva ketinggian. Gradien kedalaman pada suatu titik akan tegak lurus terhadap garis kontur, menunjukkan arah kemiringan dasar laut.
Misal digambarkan permukaan z = |xy|, beserta peta kontur dan medan gradiennya. Perhatikan bahwa vektor-vektor gradien tegak lurus terhadap kurva ketinggiam dan menunjuk ke arah peningkatan z yang terbesar.
Bayangkan Anda memiliki sebuah peta topografi gunung. Garis-garis kontur pada peta tersebut menunjukkan ketinggian yang sama. Jika Anda menggambar sebuah panah pada setiap titik pada peta yang menunjukkan arah kemiringan yang paling curam, maka panah-panah tersebut akan tegak lurus terhadap garis kontur dan akan menunjuk ke puncak gunung.
Contoh:
Diberikan paraboloid z = ¼x² + y². Tentukan kurva ketinggiannya yang melalui P(2, 1). Tentukan vektor gradien dari paraboloid di P.
Kurva ketinggian paraboloid pada ketinggian z = k adalah ¼x² + y² = k, masukkan titik P(2, 1) ke persamaan kurva ketinggian, diperoleh k = ¼.2² + 1² = 2. Jadi, kurva ketinggian yang melalui P adalah ellips ¼x² + y² = 2.
Misal f(x, y) = ¼x² + y², fx(x, y) = ½x, fy(x, y) = 2y, gradien paraboloid pada titik P(2, 1) adalah
∇f(2, 1) = fx(2, 1)i + fy(2, 1)j = i + 2j.
5. Dimensi yang Lebih Tinggi
Konsep kurva ketinggian untuk fungsi dua variabel dapat digeneralisasi menjadi permukaan ketinggian untuk fungsi tiga variabel. Jika f adalah fungsi dari tiga variabel, permukaan f(x, y, z) = k, di mana k adalah konstanta, adalah permukaan tingkat untuk f. Pada semua titik pada permukaan tingkat, nilai fungsi adalah sama, dan vektor gradien dari f(x, y, z) pada titik P(x, y, z) dalam domainnya adalah normal (tegak lurus) terhadap permukaan tingkat f yang melalui P.
Dalam masalah konduksi panas pada benda homogen, di mana w = f(x, y, z) memberikan suhu pada titik (x, y, z), permukaan tingkat f(x, y, z) = k disebut permukaan isotherm karena semua titik di atasnya memiliki suhu yang sama (k). Pada setiap titik dalam benda, panas mengalir dalam arah yang berlawanan dengan gradien (yaitu, dalam arah penurunan suhu terbesar) dan oleh karena itu tegak lurus terhadap permukaan isotherm yang melalui titik tersebut. Jika w = f(x, y, z) memberikan potensial listrik (tegangan) pada setiap titik dalam medan potensial listrik, permukaan tingkat fungsi tersebut disebut permukaan equipotensial. Semua titik pada permukaan equipotensial memiliki potensial listrik yang sama, dan arah aliran listrik adalah sepanjang gradien negatif, yaitu, dalam arah penurunan potensial terbesar.
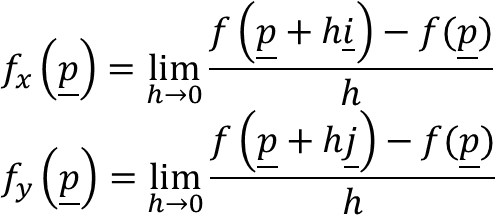













Komentar
Posting Komentar