Integral atas Daerah Bukan Persegi Panjang

1. Pengenalan

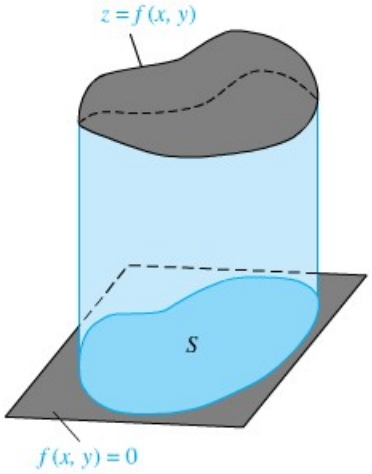
Misal S adalah sembarang himpunan tertutup dan terbatas. Kelilingi S dengan persegi panjang R yang sisi-sisinya sejajar dengan sumbu-sumbu koordinat.

Misal f(x, y) terdefinisi dan f(x, y) = 0 pada bagian dari R yang terletak di luar S.

Kita katakan f terintegralkan pada S jika dia terintegralkan pada R dan ditulis

Integral rangkap  pada himpunan S secara umum memenuhi sifat : 

(i) Linier 

(ii) Aditif (pada himpunan-himpunan yang berpotongan pada suatu kurva mulus)

(iii) Perbandingan

2. Himpunan y Sederhana dan Himpunan x Sederhana

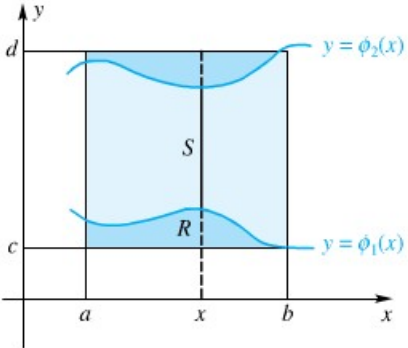
A. Himpunan y sederhana

S dikatakan himpunan y-sederhana jika terdapat φ₁ dan φ₂ yang kontinu pada [a, b] sedemikian sehingga S = {(x, y): φ₁(x) ≤ y ≤ φ₂(x), a ≤ x ≤ b}. Garis dalam arah sumbu y memotong S pada satu ruas garis atau satu titik atau tidak memotong sama sekali.

B. Himpunan x sederhana

S dikatakan himpunan x-sederhana jika terdapat ψ₁ dan ψ₂ yang kontinu pada [c, d] sedemikian sehingga S = {(x, y): ψ₁(y) ≤ x ≤ ψ₂(y), c ≤ y ≤ d}. Garis dalam arah sumbu–x memotong S pada satu ruas garis atau satu titik atau tidak memotong sama sekali.

Ciri	Himpunan x-sederhana	Himpunan y-sederhana
Garis yang memotong	Horisontal	Vertikal
Batas	ψ₁(y) ≤ x ≤ ψ₂(y)	φ₁(x) ≤ y ≤ φ₂(x)
Interval	c ≤ y ≤ d	a ≤ x ≤ b

Himpunan x sederhana lebih mudah diintegralkan terhadap x terlebih dahulu, sedangkan himpunan y sederhana lebih mudah diintegralkan terhadap y terlebih dahulu.

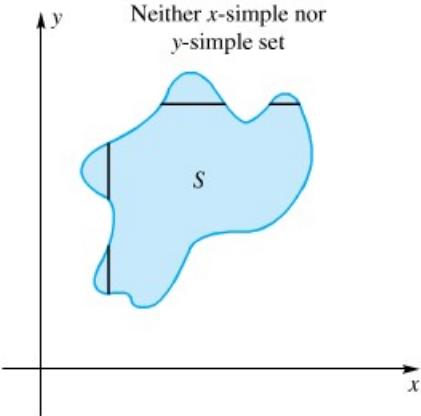
C. Himpunan yang bukan himpunan y sederhana maupun himpunan x sederhana

Himpunan yang tidak termasuk dalam kategori x-sederhana atau y-sederhana, kita tidak dapat langsung menerapkan rumus integral ganda yang sederhana untuk menghitung luas atau volume daerah tersebut. Kita perlu menggunakan teknik-teknik lain atau membagi daerah menjadi beberapa bagian yang lebih kecil yang masing-masing memenuhi syarat x-sederhana atau y-sederhana.

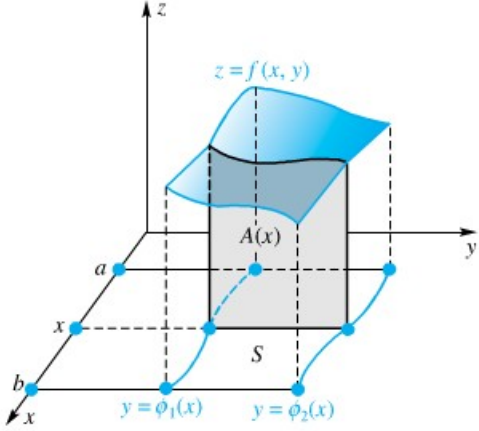
3. Menentukan Integral pada Himpunan y Sederhana atau x Sederhana

Sekarang misalkan kita ingin menghitung integral ganda dari suatu fungsi f(x, y) pada himpunan y-sederhana S. Kita bungkus S dalam sebuah persegi panjang R dan membuat f(x, y) = 0 di luar S. Kemudian

Secara umum rumus integral pada himpunan y sederhana adalah:

Adapun rumus integral pada himpunan x sederhana:

Adapun jika himpunan S bukan merupakan himpunan x-sederhana maupun y-sederhana, maka biasanya himpunan tersebut dapat dianggap sebagai gabungan dari beberapa bagian yang masing-masing merupakan himpunan x-sederhana atau y-sederhana. Integral pada masing-masing bagiannya dapat dihitung dan kemudian dijumlahkan untuk mendapatkan integral keseluruhan pada S.

Contoh Soal dan Pembahasan

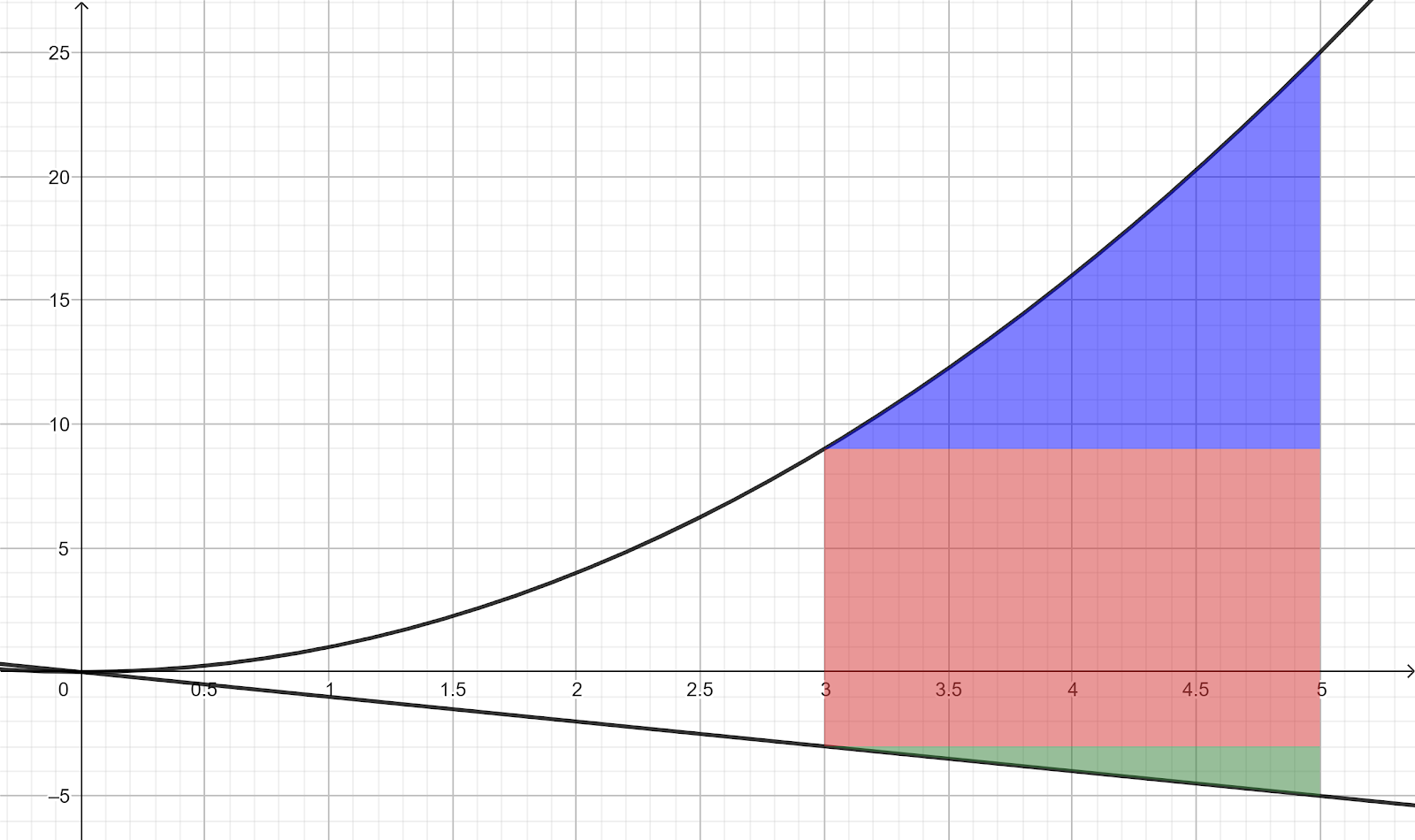
1. Diberikan daerah S berikut:

Misal daerah S dibatasi oleh kurva y = x², y = −x, x = 3, dan x = 5. Jika f(x, y) = 4x + 10y, maka tentukan volume dari ruang yang diatas S dibawah permukaan z = f(x, y).

Daerah S merupakan himpunan y sederhana dengan S = {(x, y): −x ≤ y ≤ x², 3 ≤ x ≤ 5}, sehingga lebih mudah untuk diintegralkan terhadap y terlebih dahulu

Lalu bagaimana jika diintegralkan terhadap x terlebih dahulu? kita bagi menjadi 3 bagian yang masing-masing merupakan himpunan x sederhana.

Himpunan S bukan himpunan x sederhana, tetapi dapat dibagi menjadi 3 bagian yang masing-masing himpunan x sederhana. Untuk menentukan integralnya, tentukan masing-masing bagian lalu dijumlahkan.

2. Diberikan suatu ruang di oktan I dibatasi oleh paraboloid z = x² + y² dan silinder x² + y² = 4, tentukan volumenya!

Perhatikan daerah integrasinya di bidang XOY, yaitu ¼ dari lingkaran x² + y² = 4 dan dibatasi sumbu x dan sumbu y.

Karena x² + y² = 4, kita dapat menuliskan batas kanan untuk x = sqrt(4 − y²); 0 < x < sqrt(4 − y²)

Untuk y, kita batasi 0 < y < 2

Penutup atasnya adalah paraboloid z = x² + y², ini menjadi integrannya.

Ambil substitusi trigonometri 

Misal 𝑦 = 2.sin(⁡𝑡) → 𝑑𝑦 = 2.cos(⁡𝑡) 𝑑𝑡

𝑦 = 0 → 𝑡 = arcsin(⁡0) = 0

𝑦 = 2 → 𝑡 = arcsin(2/2) = 𝜋∕2

Jadi, volumenya adalah 2𝜋.