Aturan Sinus dan Aturan Kosinus

1. Aturan Sinus
Perhatikan gambar berikut:
Diberikan segitiga ABC dan titik D terletak pada sisi BC sehingga AD merupakan garis tinggi.
Perhatikan segitiga ABD, siku-siku di D
AD = AB.sin(B) = c.sin(B) ...(i)
Perhatikan segitiga ACD, siku-siku di D
AD = AC.sin(C) = b.sin(C) ...(ii)
Dari (i) dan (ii) diperoleh:
AD = AD
c.sin(B) = b.sin(C)
c/sin(C) = b/sin(B) ...(iii)
Selanjutnya perhatikan:
Misal titik E terletak pada sisi AC sehingga BE merupakan garis tinggi.
Perhatikan segitiga ABE, siku-siku di E
AE = AB.sin(A) = c.sin(A) ...(iv)
Perhatikan segitiga ACE, siku-siku di E
AE = BC.sin(C) = a.sin(C) ...(v)
Dari (iv) dan (v) diperoleh:
AE = AE
c.sin(A) = a.sin(C)
c/sin(C) = a/sin(A) ...(vi)
Dari (iii) dan (vi) diperoleh:
a/sin(A) = b/sin(B) = c/sin(C)
Selanjutnya ingat kembali rumus jari-jari lingkaran luar:
masukkan persamaan (i)
sehingga diperoleh:
bentuk persamaan terakhir ini disebut sebagai aturan sinus.

2. Aturan Kosinus
Perhatikan gambar berikut:
Menurut dalil proyeksi, berlaku:
c² = a² + b² – 2bp
sedangkan p = a.cos(C), sehingga:
c² = a² + b² – 2.a.b.cos(C)
secara analog, berlaku untuk ketiga sisi:
c² = a² + b² – 2.a.b.cos(C)
b² = a² + c² – 2.a.c.cos(B)
a² = b² + c² – 2.b.c.cos(A)
Untuk mencari nilai kosinus, berikut ini rumusnya:
Catatan:
Ingat kembali sudut berelasi, bahwa sin(180° – α) = sin(α). Hal ini berakibat jika diketahui nilai sinus, akan terdapat dua besar sudut yang memenuhinya, satu sudut lancip dan satu sudut tumpul.
Sedangkan cos(180° – α) = –cos(α). Sehingga kita bisa memastikan besar sudutnya jika diketahui nilai kosinus. Untuk kosinus positif, sudut di kuadran I, dan untuk kosinus negatif, sudut di kuadran II.
Mempertimbangkan ini, lebih aman menggunakan aturan kosinus untuk mencari besar sudut.
Berikut video berhati-hati menggunakan aturan sinus:

3. Aturan Tangen
A. Rumus Napler
Ingat kembali aturan sinus:
sehingga:
a = 2R.sin(A),    b = 2R.sin(B),    c = 2R.sin(C)
sehingga:
B. Identitas Tripel Tangen
A + B + C = 180°
C = 180° – (A + B)
tan(C) = tan[180° – (A + B)]
= –tan(A + B)
sehingga:
tan(C).[tan(A).tan(B) – 1] = tan(A) + tan(B)
tan(A).tan(B).tan(C) – tan(C) = tan(A) + tan(B)
∴ tan(A).tan(B).tan(C) = tan(A) + tan(B) + tan(C)

4. Aturan Kotangen
A. Aturan Kotangen
Perhatikan gambar berikut:
diperoleh:
cot(½A) = (s – a)/r, juga:
cot(½B) = (s – b)/r,
cot(½C) = (s – c)/r
sehingga:
B. Identitas Tripel Kotangen
A + B + C = 180°
½A + ½B + ½C = 90°
½C = 90° – (½A + ½B)
tan(½C) = tan[90° – (½A + ½B)]
tan(½C) = cot(½A + ½B)
tan(½C) = [cot(½A).cot(½B) – 1]/[cot(½A) + cot(½B)]
cot(½A) + cot(½B) = [cot(½A).cot(½B) – 1].cot(½C)
cot(½A) + cot(½B) = cot(½A).cot(½B).cot(½C) – cot(½C)
∴ cot(½A) + cot(½B) + cot(½C) = cot(½A).cot(½B).cot(½C)
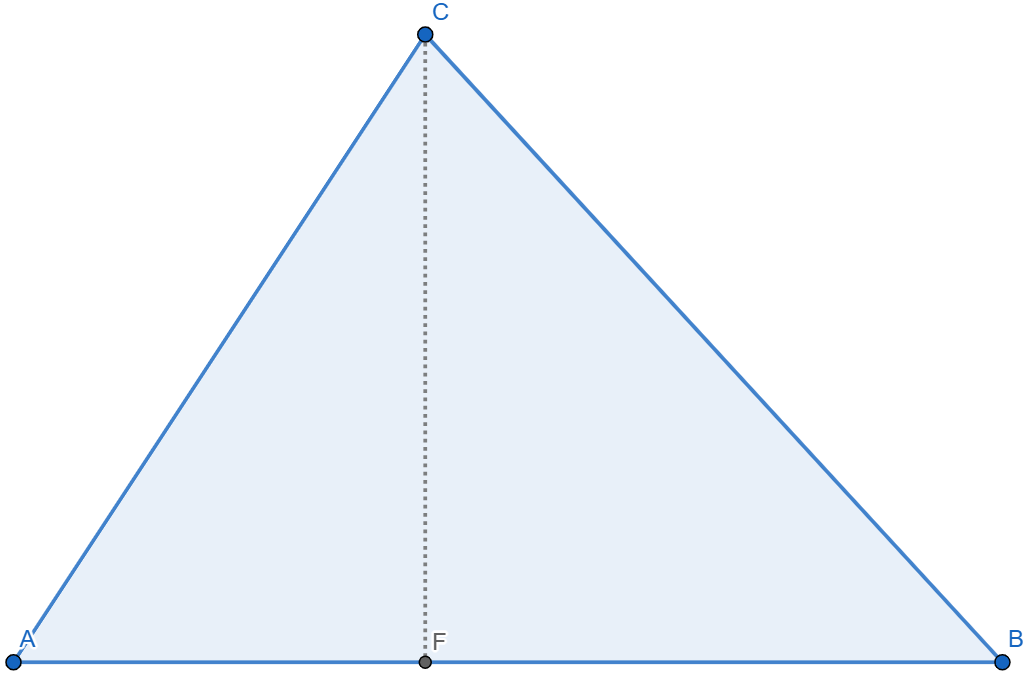
C. Perbandingan Panjang Sisi dan Tinggi
Perhatikan gambar berikut:
Diberikan segitiga ABC dan titik F pada sisi AB sehingga CF merupakan garis tinggi.
cot(A) = |AF|/|CF|,    cot(B) = |BF|/|CF|
cot(A) + cot(B) = (|AF| + |BF|)/|CF| = |AB|/|CF|
cot(A) + cot(B) = c/|CF|
Jumlah kotangen dua sudut pada segitiga sama dengan perbandingan panjang sisi segitiga terhadap tingginya.
D. Jumlah Hasil Kali Sepasang
cot(A).cot(B) + cot(A).cot(C) + cot(B).cot(C)
= cot(A).cot(B) + cot(C).[cot(A) + cot(B)]
= cot(A).cot(B) + cot[180° – (A + B)].[cot(A) + cot(B)]
= cot(A).cot(B) – cot(A + B).[cot(A) + cot(B)]
= cot(A).cot(B) – [cot(A).cot(B) – 1]/[cot(A) + cot(B)] × [cot(A) + cot(B)]
= cot(A).cot(B) – [cot(A).cot(B) – 1]
= 1
Jadi, cot(A).cot(B) + cot(A).cot(C) + cot(B).cot(C) = 1

5. Rumus De Lambre - Mollweide
A. Rumus Mollweide 1
Jadi, diperoleh:
B. Rumus Mollweide 2
Jadi, diperoleh:

Contoh Soal
1. Diberikan segitiga ABC dengan besar ∠A = 30°, ∠C = 105° dan panjang BC = 10 cm. Maka panjang AB dan AC adalah …
∠B = 180° – (∠A + ∠C) = 180° – (30° + 105°) = 45°
menurut aturan sinus, berlaku:
Panjang AC
Panjang AB
Jadi, panjang AB adalah 19,319 cm dan panjang AC adalah 14,142 cm.

2. Perhatikan gambar berikut:
Tentukan panjang sisi BC dan besar sudut ABC.
• Panjang sisi AC
• Panjang sisi BC
• Besar sudut ABC

3. Dari pelabuhan P, kapal A berlayar ke arah 45° dengan kecepatan 30 km/jam, sedangkan kapal B berlayar ke arah 345° dengan kecepatan 35 km/jam. Berapakah jarak kapal A dan kapal B setelah 2 jam?
Diketahui kapal A berlayar ke arah 45° dan kapal B berlayar ke arah 345°, sudut antara keduanya adalah 345° – 45° = 300°, principalnya 60°.
Kapal A berlayar dengan kecepatan 30 km/jam, sehingga setelah 2 jam, jarak tempuhnya adalah 60km.
Kapal B berlayar dengan kecepatan 35 km/jam, sehingga setelah 2 jam, jarak tempuhnya adalah 70km.
Kuadrat jarak antara keduanya adalah:
60² + 70² – 2.60.70.cos(60°) = 3600 + 4900 – 8400.½ = 4300
Jarak antara keduanya adalah sqrt(4300) ≈ 65,574 km.

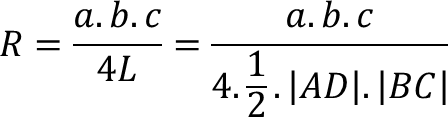
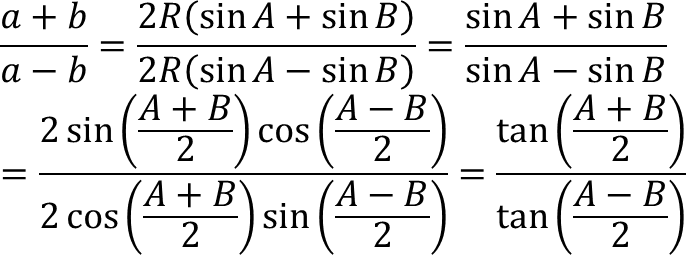
Komentar

Posting Komentar

Postingan populer dari blog ini

Rotasi Baru (Komposisi Geseran dan Rotasi)

Gambar
1. Komposisi Geseran dengan Rotasi Untuk sebarang titik A, B, P, dan besar sudut θ, selalu dapat ditemukan titik C sehingga: a. S AB R P, θ  = R C, θ   Misal terdapat dua garis sejajar r dan s dengan jarak antara keduanya adalah ½|AB|, sehingga dipenuhi S AB  = M r M s . Misal terdapat garis t yang memotong s di P dengan sudut antara s dan t adalah ½θ, sehingga dipenuhi R P, θ  = M s M t . Kita dapat menguraikan S AB R P, θ  = (M r M s )(M s M t ) = M r M s M s M t   = M r IM t   = M r M t , karena r sejajar s, sudut antara r dan t juga ½θ, misal r dan t berpotongan di C = R C, θ   b. R P, θ S AB  = R C, θ   Misal terdapat dua garis sejajar r dan s dengan jarak antara keduanya adalah ½|AB|, sehingga dipenuhi S AB  = M s M r . Misal terdapat garis t yang memotong s di P dengan sudut antara s dan t adalah ½θ, sehingga dipenuhi R P, θ  = M t M s . Kita dapat menguraikan R P, θ S AB  = M t M s M s M r   = M t ...
Read more »

2024: Aritmatika Jilid XII

Gambar
Aritmatika adalah event tahunan yang diselenggarakan oleh Himpunan Mahasiswa Pendidikan Matematika Universitas Sebelas Maret Surakarta. Dalam Aritmatika jilid XII terdapat tiga rangkaian acara yaitu Lomba Olimpiade Matematika, Lomba Media Pembelajaran Matematika Tingkat Nasional, dan Lomba Microteching tingkat Nasional. 1. Olimpiade Matematika Lomba ini diperuntukkan bagi siswa SMP, SMA, atau sederajat dari seluruh Indonesia. Lomba ini bersifat individu, tidak berkelompok. Setiap sekolah dibolehkan mengirimkan lebih dari satu delegasi. Timeline untuk olimpiade ini sebagai berikut: 1 s/d 20 Juli 2024: Pendaftaran Gelombang 1, dengan biaya pendaftaran Rp 40.000 untuk SMP dan Rp 45.000 untuk SMA. 22 Juli s/d 10 Agustus 2024: Pendaftaran Gelombang 2, dengan biaya pendaftaran Rp 45.000 untuk SMP dan Rp 50.000 untuk SMA. 12 s/d 25 Agustus 2024: Pendaftaran Gelombang 3, dengan biaya pendaftaran Rp 50.000 untuk SMP dan Rp 55.000 untuk SMA. 1 September 2024: Technical Meeting (Online) 7 Septemb...
Read more »

Kombinasi Linear Vektor dan Rentang

Gambar
1. Ruang Penyelesaian untuk Sistem-Sistem Homogen Jika A x = b adalah suatu sistem persamaan linear, maka setiap vektor x yang memenuhi persamaan ini disebut suatu vektor penyelesaian dari sistem tersebut. Teorema berikut ini menunjukkan bahwa vektor penyelesaian dari suatu sistem linear homogen membentuk suatu ruang vektor, yang akan kita sebut sebagai ruang penyelesaian dari sistem tersebut. Teorema: "Jika A x = 0 adalah suatu sistem linear homogen dari m persamaan dalam n variabel, maka himpunan vektor penyelesaiannya adalah suatu subruang dari R-n". Bukti: Anggap W adalah himpunan vektor penyelesaian. Paling tidak ada satu vektor dalam W, yaitu 0 . Untuk menunjukkan bahwa W tertutup terhadap penjumlahan dan perkalian skalar, kita harus menunjukkan bahwa jika x dan x ' adalah sembarang vektor-vektor penyelesaian dan k adalah sembarang skalar, maka x + x ' dan k x juga merupakan vektor-vektor penyelesaian. Akan tetapi, jika x dan x ' adalah vektor-vekt...
Read more »