Barisan Aritmetika Bertingkat

1. Bentuk Polinomial untuk Barisan Aritmetika Bertingkat

Misal diberikan barisan

1, 3, 8, 20, 43, 81, 138, ...

beda antar suku tidak sama, yaitu

2, 5, 12, 23, 38, 57, ...

ulangi langkah yang sama

3, 7, 11, 15, 19, ...

4, 4, 4, 4, ... beda sudah sama

barisan ini memerlukan 3 kali perulangan untuk menjadi konstan.

Secara umum, barisan aritmatika bertingkat dapat dirumuskan menggunakan polinomial dengan derajatnya sama dengan banyak perulangan sehingga menjadi barisan yang konstan. Untuk koefisiennya bisa ditentukan menggunakan sistem persamaan linear.

Misal banyak perulangannya adalah m, rumus suku ke-n pada barisan dapat dinyatakan menggunakan polinomial berderajat m, untuk koefisiennya ditentukan menggunakan SPL m + 1 variabel.

Untuk contoh diatas, karena terjadi 3 kali perulangan untuk menjadi konstan, barisan tersebut dapat dinyatakan dalam polinomial berderajat 3, kita bisa memisalkan:

Uₙ = an³ + bn² + cn + d

U₁ = a.1³ + b.1² + c.1 + d = a + b + c + d

U₂ = a.2³ + b.2² + c.2 + d = 8a + 4b + 2c + d

U₃ = a.3³ + b.3² + c.3 + d = 27a + 9b + 3c + d

U₄ = a.4³ + b.4² + c.4 + d = 64a + 16b + 4c + d

Terbentuklah SPL 4 variabel

a + b + c + d = 1 (i)

8a + 4b + 2c + d = 3 (ii)

27a + 9b + 3c + d = 8 (iii)

64a + 16b + 4c + d = 20 (iv)

(ii) − (i) → 7a + 3b + c = 2 (v)

(iii) − (ii) → 19a + 5b + c = 5 (vi)

(iv) − (iii) → 37a + 7b + c = 12 (vii)

(vi) − (v) → 12a + 2b = 3 (viii)

(vii) − (vi) → 18a + 2b = 7 (ix)

(ix) − (viii) → 6a = 4 ↔ a = ⅔, masukkan ke (viii)

12.⅔ + 2b = 3 ↔ b = −5/2, masukkan ke (v)

7.⅔ + 3(−5/2) + c = 2 ↔ c = 29/6, masukkan ke (i)

⅔ − 5/2 + 29/6 + d = 1 ↔ d = −2

Telah diperoleh nilai untuk koefisiennya, sehingga barisan ini dapat dirumuskan:

Uₙ = ⅔n³ − (5/2)n² + (29/6)n − 2

Dengan ini, misal kita ingin menentukan suku ke-12, kita dapat mencari dengan memasukkan n = 12 ke rumus Uₙ

U₁₂ = ⅔.12³ − (5/2).12² + (29/6).12 − 2 = 848

Jadi, suku ke-12 adalah 848.

2. Deret Aritmetika Bertingkat dalam Polinomial

Misal suatu barisan aritmatika dengan tingkat m, rumus untuk deretnya menjadi bertingkat m + 1.

Misal suatu barisan

1, 3, 8, 20, 43, 81, 138, ...

barisan ini bertingkat 3

Deret dari barisan ini dapat dinyatakan:

1, 4, 12, 32, 75, 156, 294, ...

Deretnya membentuk barisan baru, dengan tingkat 4, untuk koefisiennya bisa dicari menggunakan SPL 5 variabel berikut:

a + b + c + d + e = 1 (i)

16a + 8b + 4c + 2d + e = 4 (ii)

81a + 27b + 9c + 3d + e = 12 (iii)

256a + 64b + 16c + 4d + e = 32 (iv)

625a + 125b + 25c + 5d + e = 75 (v)

apabila diselesaikan, akan diperoleh a = ⅙, b = −½, c = 4/3, d = 0, e = 0

sehingga Sₙ = ⅙n⁴ − ½n³ + (4/3)n²

3. Menentukan Rumus Uₙ berdasarkan Rumus Sₙ

Ingat kembali bahwa:

Sₙ = U₁ + U₂ + U₃ + U₄ + ... + Uₙ₋₁ + Uₙ

Sₙ₋₁ = U₁ + U₂ + U₃ + U₄ + ... + Uₙ₋₁

Sehingga diperoleh:

Uₙ = Sₙ − Sₙ₋₁

dengan ini, lebih mudah mencari rumus Uₙ daripada rumus Sₙ.

Contoh:

Diberikan Sₙ = ⅙n⁴ − ½n³ + (4/3)n², tentukan rumus untuk Uₙ.

Uₙ = Sₙ − Sₙ₋₁

= ⅙n⁴ − ½n³ + (4/3)n² − ⅙(n − 1)⁴ + ½(n − 1)³ + (4/3)(n − 1)²

= ⅙(4n³ − 6n² + 4n − 1) − ½(3n² − 3n + 1) + (4/3)(2n − 1)

= ⅔n³ + (−1 − 3/2)n² + (⅔ + 3/2 + 8/3)n − ⅙ − ½ − 4/3

= ⅔n³ − (5/2)n² + (29/6)n − 2

4. Rumus Uₙ untuk Sₙ berbentuk Suku Tunggal

Beberapa contoh ini akan cukup membantu:

A. Untuk Sₙ = n

Uₙ = Sₙ − Sₙ₋₁ = n − (n − 1) = 1

B. Untuk Sₙ = n²

Uₙ = Sₙ − Sₙ₋₁ = n² − (n − 1)² = n² − (n² − 2n + 1) = 2n − 1

C. Untuk Sₙ = n³

Uₙ = Sₙ − Sₙ₋₁ = n³ − (n − 1)³ = n³ − (n³ − 3n² + 3n − 1) = 3n² − 3n + 1

D. Untuk Sₙ = n⁴

Uₙ = Sₙ − Sₙ₋₁ = n⁴ − (n − 1)⁴ = n⁴ − (n⁴ − 4n³ + 6n² − 4n + 1) = 4n³ − 6n² + 4n − 1

E. Untuk Sₙ = n⁵

Uₙ = Sₙ − Sₙ₋₁ = n⁵ − (n − 1)⁵ = n⁵ − (n⁵ − 5n⁴ + 10n³ − 10n² + 5n − 1) = 5n⁴ − 10n³ + 10n² − 5n + 1

dan seterusnya. Secara umum dapat ditentukan menggunakan binomial:

5. Rumus Jumlah Khusus (Rumus Faulhaber)

Misal suatu barisan bersuku tunggal, berikut ini beberapa contoh rumus jumlah khusus:

A. Rumus jumlah khusus untuk Uₙ = 1

Sₙ = 1 + 1 + 1 + ... + 1, sebanyak n, sehingga

Sₙ = n

B. Rumus jumlah khusus untuk Uₙ = n

Sₙ = 1 + 2 + 3 + ... + n

Ingat kembali bahwa 1 + 3 + 5 + ... + (2n − 1) = n², bagi masing-masing ruas dengan 2

1/2 + 3/2 + 5/2 + ... + (n − 1/2) = n²/2 ...(i)

Ingat kembali bahwa 1 + 1 + 1 + ... + 1 = n, bagi masing-masing ruas dengan 2

½ + ½ + ½ + ... + ½ = n/2 ...(ii)

(i) + (ii) → 1 + 2 + 3 + ... + n = n²/2 + n/2, boleh juga dituliskan

1 + 2 + 3 + ... + n = (n² + n)/2, dapat difaktorkan

1 + 2 + 3 + ... + n = n(n + 1)/2

C. Rumus jumlah khusus untuk Uₙ = n²

Sₙ = 1 + 2² + 3² + ... + n² = 1 + 4 + 9 + ... + n²

Ingat kembali bahwa 1 + 7 + 19 + ... + (3n² − 3n + 1) = n³, bagi masing-masing ruas dengan 3

1/3 + 7/3 + 19/3 + ... + (n² − n + 1/3) = n³/3 ...(i)

Ingat kembali bahwa 1 + 3 + 5 + ... + (2n − 1) = n², bagi masing-masing ruas dengan 2

1/2 + 3/2 + 5/2 + ... + (n − 1/2) = n²/2 ...(ii)

(i) + (ii) → 5/6 + 23/6 + 53/6 + ... + (n² − 1/6) = n³/3 + n²/2 ...(iii)

Ingat kembali bahwa 1 + 1 + 1 + ... + 1 = n, bagi masing-masing ruas dengan 6

1/6 + 1/6 + 1/6 + ... + 1/6 = n/6 ...(iv)

(iii) + (iv) → 1 + 4 + 9 + ... + n² = n³/3 + n²/2 + n/6, boleh juga dituliskan

1 + 4 + 9 + ... + n² = (2n³ + 3n² + n)/6, dapat difaktorkan

1 + 4 + 9 + ... + n² = n(n + 1)(2n + 1)/6

D. Rumus jumlah khusus untuk Uₙ = n³

Sₙ = 1 + 2³ + 3³ + ... + n³ = 1 + 8 + 27 + ... + n³

Ingat kembali bahwa 1 + 15 + 65 + ... + (4n³ − 6n² + 4n − 1) = n⁴, bagi masing-masing ruas dengan 4

1/4 + 15/4 + 65/4 + ... + (n³ − (3/2)n² + n − 1/4) = n⁴/4 ...(i)

Ingat kembali bahwa 1 + 7 + 19 + ... + (3n² − 3n + 1) = n³, bagi masing-masing ruas dengan 2

1/2 + 7/2 + 19/2 + ... + ((3/2)n² − (3/2)n + 1/2) = n³/2 ...(ii)

(i) + (ii) → 3/4 + 29/4 + 103/4 + ... + (n³ − n/2 + 1/4) = n⁴/4 + n³/2 ...(iii)

Ingat kembali bahwa 1 + 3 + 5 + ... + (2n − 1) = n², bagi masing-masing ruas dengan 4

1/4 + 3/4 + 5/4 + ... + (n/2 − 1/4) = n²/4 ...(iv)

(iii) + (iv) → 1 + 8 + 27 + ... + n³ = n⁴/4 + n³/2 + n²/4, boleh juga dituliskan

1 + 8 + 27 + ... + n³ = (n⁴ + 2n³ + n²)/4, dapat difaktorkan

1 + 8 + 27 + ... + n³ = n²(n + 1)²/4

E. Rumus jumlah khusus untuk Uₙ = n⁴

Sₙ = 1⁴ + 2⁴ + 3⁴ + ... + n⁴ = 1 + 16 + 81 + ... + n⁴

Ingat kembali bahwa 1 + 31 + 211 + ... + (5n⁴ − 10n³ + 10n² − 5n + 1) = n⁵, bagi masing-masing ruas dengan 5

1/5 + 31/5 + 211/5 + ... + (n⁴ − 2n³ + 2n² − n + 1/5) = n⁵/5 ...(i)

Ingat kembali bahwa 1 + 15 + 65 + ... + (4n³ − 6n² + 4n − 1) = n⁴, bagi masing-masing ruas dengan 2

1/2 + 15/2 + 65/2 + ... + (2n³ − 3n² + 2n − 1/2) = n⁴/2 ...(ii)

(i) + (ii) → 7/10 + 137/10 + 747/10 + ... + (n⁴ − n² + n − 3/10) = n⁵/5 + n⁴/2 ...(iii)

Ingat kembali bahwa 1 + 7 + 19 + ... + (3n² − 3n + 1) = n³, bagi masing-masing ruas dengan 3

1/3 + 7/3 + 19/3 + ... + (n² − n + 1/3) = n³/3 ...(iv)

(iii) + (iv) → 31/30 + 481/30 + 2431/30 + ... + (n⁴ + 1/30) = n⁵/5 + n⁴/2 + n³/3 ...(v)

Ingat kembali bahwa 1 + 1 + 1 + ... + 1 = n, bagi masing-masing ruas dengan 30

1/30 + 1/30 + 1/30 + ... + 1/30 = n/30 ...(vi)

(v) − (vi) → 1 + 16 + 81 + ... + n⁴ = n⁵/5 + n⁴/2 + n³/3 − n/30, boleh juga dituliskan

1 + 16 + 81 + ... + n⁴ = (6n⁵ + 15n⁴ + 10n³ − n)/30, dapat difaktorkan

1 + 16 + 81 + ... + n⁴ = n(n + 1)(2n + 1)(3n² + 3n − 1)/30

Berikut beberapa rumus jumlah khusus Faulhaber:

Minfor mempersilahkan Sixtyfourians jika ingin mencoba.

6. Bentuk Binomial untuk Barisan Aritmetika Bertingkat

Misal diberikan barisan

1, 3, 8, 20, 43, 81, 138, ...

beda antar suku tidak sama, yaitu

2, 5, 12, 23, 38, 57, ...

ulangi langkah yang sama

3, 7, 11, 15, 19, ...

4, 4, 4, 4, ... beda sudah sama

barisan ini memerlukan 3 kali perulangan untuk menjadi konstan.

Kita dapat menyusun secara miring, sebagai berikut:

Bentuknya agak mirip dengan segitiga Pascal. Ini berarti kita dapat menyatakan barisan aritmetika bertingkat dalam bentuk binomial.

Barisan 3, 7, 11, 15, 19, ... dapat dinyatakan dengan

Uₙ = 3 + 4(n − 1) = 3 + 4.C(n − 1, 1)

Barisan 2, 5, 12, 23, 38, 57, ... dapat dinyatakan dengan

Uₙ = 2 + 3 + 7 + 11 + 15 + 19 + ...

Ingat kembali deret binomial, sehingga dapat dinyatakan:

1, 3, 8, 20, 43, 81, 138, ... dapat dinyatakan dengan

Uₙ = 1 + 2 + 5 + 12 + 23 + 38 + 57 + ...

Ingat kembali deret binomial, sehingga dapat dinyatakan:

boleh juga:

Jika kita amati, rumus suku ke-n dalam bentuk binomial adalah jumlah suku-suku pertama di setiap tingkatan dengan masing-masing dikalikan kombinasi n − 1 dengan tingkatannya.

7. Bentuk Binomial untuk Deret Aritmatika Bertingkat

Misal suatu barisan

1, 3, 8, 20, 43, 81, 138, ...

barisan ini bertingkat 3

Deret dari barisan ini dapat dinyatakan:

1, 4, 12, 32, 75, 156, 294, ...

Deretnya membentuk barisan baru, yang kita dapat nyatakan dalam binomial

1, 4, 12, 32, 75, 156, 294, ...

3, 8, 20, 43, 81, 138, ...

5, 12, 23, 38, 57, ...

7, 11, 15, 19, ...

4, 4, 4, ...

Deretnya membentuk barisan baru dengan suku pertamanya sama dengan suku pertama barisan semula, sedangkan suku pertama untuk tingkatan selanjutnya sama dengan suku kedua barisan semula.

8. Bentuk Binomial untuk Uₙ Bersuku Tunggal

A. Bentuk binomial untuk Uₙ = 1

1, 1, 1, ... dalam bentuk binomial

B. Bentuk binomial untuk Uₙ = n

1, 2, 3, ... 

1, 1, ...

dalam bentuk binomial

C. Bentuk binomial untuk Uₙ = n²
1, 4, 9, 16, 25, ...

3, 5, 7, 9, ...

2, 2, 2, ...

dalam bentuk binomial

D. Bentuk binomial untuk Uₙ = n³
1, 8, 27, 64, 125, 216, ...

7, 19, 37, 61, 91, ...

12, 18, 24, 30, ...

6, 6, 6, ...

dalam bentuk binomial

E. Bentuk binomial untuk Uₙ = n⁴
1, 16, 81, 256, 625, 1296, 2401, ...

15, 65, 175, 369, 671, 1105, ...

50, 110, 194, 302, 434, ...

60, 84, 108, 132, ...

24, 24, 24, ...

F. Bentuk binomial untuk Uₙ = n⁵

1, 32, 243, 1024, 3125, 7776, 16807, 32768, ...

31, 211, 781, 2101, 4651, 9031, 15961, ...

180, 570, 1320, 2550, 4380, 6930, ...

390, 750, 1230, 1830, 2550, ...

360, 480, 600, 720, ...

120, 120, 120, ...

Beberapa bentuk binomial untuk suku tunggal:

Minfor mempersilahkan Sixtyfourians jika ingin mencoba.

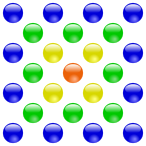
9. Bilangan Poligon Non-Sentral

Perhatikan pola berikut:

Bilangan segitiga: 1, 3, 6, 10, 15, ... = 1 + 2 + 3 + 4 + 5 + ...

Bilangan kuadrat/persegi: 1, 4, 9, 16, 25, ... = 1 + 3 + 5 + 7 + 9 + ...

Bilangan segilima: 1, 5, 12, 22, 35, ... = 1 + 4 + 7 + 10 + 13 + ...

Bilangan segienam: 1, 6, 15, 28, 45, ... = 1 + 5 + 9 + 13 + 17 + ...

Rumus suku ke-n untuk bilangan segi-s adalah

P(s, n) = 1 + (s − 1) + (2s − 3) + ... + ((n − 1)s − (2n − 3))

P(s, n) = 1 + s(1 + 2 + 3 + ... + (n − 1)) − (1 + 3 + 5 + ... + (2n − 3))

P(s, n) = 1 + sn(n − 1)/2 − (n − 1)² = 1 + sn(n − 1)/2 − n² + 2n − 1 = sn(n − 1)/2 − n² + 2n

P(s, n) = [sn² − sn − 2n² + 4n]/2

P(s, n) = [(s − 2)n² − (s − 4)n]/2

Contoh:

Tentukan suku ke-10 dari bilangan segi 8

P(s, n) = [(s − 2)n² − (s − 4)n]/2, s = 8, n = 10

P(8, 10) = [(8 − 2).10² − (8 − 4).10]/2 = 280

Jadi, suku ke-10 dari bilangan segi 8 adalah 280.

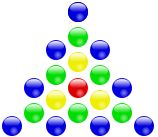
10. Bilangan Poligon Sentral

Bilangan segitiga sentral: Uₙ = 1 + 3(1 + 2 + 3 + ... + (n − 1))

Bilangan persegi sentral: Uₙ = 1 + 4(1 + 2 + 3 + ... + (n − 1))

Bilangan segilima sentral: Uₙ = 1 + 5(1 + 2 + 3 + ... + (n − 1))

Bilangan segienam sentral: Uₙ = 1 + 6(1 + 2 + 3 + ... + (n − 1))

Rumus suku ke-n untuk bilangan segi-s sentral adalah:

P(s, n) = 1 + s(1 + 2 + 3 + ... + (n − 1)) = 1 + sn(n − 1)/2

Contoh:

Tentukan suku ke-10 dari bilangan segi 6 sentral.

P(6, 10) = 1 + 6.10.9/2 = 271