Deret Trigonometri
1. Deret Sinus
Misal suatu barisan sinus:
sin(a), sin(a + b), sin(a + 2b), ..., sin(a + (n − 1)b)
deret yang terbentuk dari barisan ini adalah:
Sₙ = sin(a) + sin(a + b) + sin(a + 2b) + ... + sin(a + (n − 1)b)
kalikan masing-masing suku dengan 2.sin(b/2), terbentuk telescoping series (deret saling habis)
2.sin(b/2).sin(a) = cos(a − b/2) − cos(a + b/2)
2.sin(b/2).sin(a + b) = cos(a + b/2) − cos(a + 3b/2)
2.sin(b/2).sin(a + 2b) = cos(a + 3b/2) − cos(a + 5b/2)
...
2.sin(b/2).sin[a + (n − 1)b] = cos[a + (n − 3/2)b] − cos[a + (n − 1/2)b]
jumlahkan sehingga diperoleh:
2.sin(b/2).Sₙ = cos(a − b/2) − cos[a + (n − 1/2)b]
2.sin(b/2).Sₙ = 2.sin(a + ½(n − 1)b).sin(nb/2)
sehingga:
Misal suatu barisan sinus:
cos(a), cos(a + b), cos(a + 2b), ..., cos(a + (n − 1)b)
deret yang terbentuk dari barisan ini adalah:
Sₙ = cos(a) + cos(a + b) + cos(a + 2b) + ... + cos(a + (n − 1)b)
kalikan masing-masing suku dengan 2.sin(b/2), terbentuk telescoping series (deret saling habis)
2.sin(b/2).cos(a) = sin(a + b/2) − sin(a − b/2)
2.sin(b/2).cos(a + b) = sin(a + 3b/2) − sin(a + b/2)
2.sin(b/2).cos(a + 2b) = sin(a + 5b/2) − sin(a + 3b/2)
...
2.sin(b/2).cos[a + (n − 1)b] = sin[a + (n − 1/2)b] − sin[a + (n − 3/2)b]
jumlahkan sehingga diperoleh:
2.sin(b/2).Sₙ = sin[a + (n − 1/2)b] − sin(a − b/2)
2.sin(b/2).Sₙ = 2.cos(a + ½(n − 1)b).sin(nb/2)
Tunjukkan bahwa p(n) benar untuk n = 1
Akan ditunjukkan bahwa p(n) juga benar untuk n = k + 1
berarti p(n) juga benar untuk n = k + 1.
Karena telah ditunjukkan bahwa p(n) benar untuk n = 1, dan telah diasumsikan bahwa p(n) benar untuk n = k, sehingga dapat ditunjukkan bahwa p(n) benar untuk n = k + 1. Oleh karena itu, p(n) benar untuk setiap n bilangan asli.
berarti p(n) juga benar untuk n = k + 1.
Karena telah ditunjukkan bahwa p(n) benar untuk n = 1, dan telah diasumsikan bahwa p(n) benar untuk n = k, sehingga dapat ditunjukkan bahwa p(n) benar untuk n = k + 1. Oleh karena itu, p(n) benar untuk setiap n bilangan asli.
Contoh Soal
1. sin²(a) + sin²(2a) + sin²(3a) + ... + sin²(na)
untuk menentukannya, lakukan reduksi pangkat, dimana sin²(a) = [1 – cos(2a)]/2
Sₙ = [1 – cos(2a)]/2 + [1 – cos(4a)]/2 + [1 – cos(6a)]/2 + ... + [1 – cos(2na)]/2
= n/2 – [cos(2a) + cos(4a) + ... + cos(2na)]/2
= n/2 – cos(2a + (n − 1)a).sin(na)/[2.sin(a)]
= n/2 – cos[(n + 1).a].sin(na)/[2.sin(a)]
2. cos³(α) + cos³(2α) + cos³(3α) + ... + cos³(nα)
untuk menentukannya, lakukan reduksi pangkat, dimana cos³(α) = [3.cos(α) + cos(3α)]/4
Sₙ = [3.cos(α) + cos(3α)]/4 + [3.cos(2α) + cos(6α)]/4 + ... + [3.cos(nα) + cos(3nα)]/4
= ¾.[cos(α) + cos(2α) + ... + cos(nα)] + ¼.[cos(3α) + cos(6α) + ... + cos(3nα)]
= ¾.cos[½.(n + 1)α].sin(½nα)/sin(½α) + ¼.cos[(3/2).(n + 1)α].sin[(3/2)nα]/sin[(3/2)α]
3. Hitunglah [√3 + tan(1°)].[√3 + tan(2°)].[√3 + tan(3°)]…[√3 + tan(29°)]
[√3 + tan(1°)].[√3 + tan(2°)].[√3 + tan(3°)]…[√3 + tan(29°)]
= [tan(60°) + tan(1°)].[tan(60°) + tan(2°)].[tan(60°) + tan(3°)]…[tan(60°) + tan(29°)]

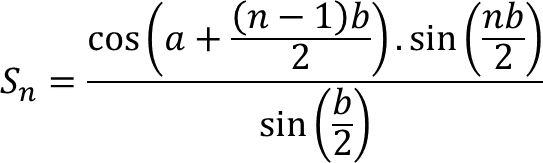




Komentar
Posting Komentar