Fungsi Densitas Probabilitas dan Fungsi Distribusi Kumulatif
1. Fungsi Densitas Probabilitas untuk Variabel Random Diskrit
Misalkan Ωx adalah ruang dari variabel random diskrit X, maka fungsi f dari Ωx ke R dinamakan fungsi densitas probabilitas (FDP) dari variabel random X yang dinotasikan f(x) jika dipenuhi :
1. (∀x). f(x) ≥ 0
Nilai fungsi tak pernah negatif.
2. Σ f(x) = 1
Jumlah seluruh peluangnya adalah 1.
Misal X merupakan variabel random diskrit dengan FDP f(x)
1. f(x) = P(X = x)
2. Untuk setiap A ⊆ Ωx, peluang terjadinya kejadian A adalah
Diketahui varibel random X. Jika f(x) merupakan fungsi dari Ωx ke R yang didefinisikan oleh
• Untuk x = 1, 2, 3, ..., nilai f(x) selalu positif, karena bilangan positif dipangkatkan berapapun selalu positif, sedangkan untuk selainnya bernilai 0, sehingga nilai f(x) tak pernah negatif.
• Jumlah seluruh peluangnya adalah:
Karena nilai f(x) tidak pernah negatif dan jumlah seluruh peluangnya adalah 1, f(x) merupakan FDP.
b. Tentukan P(A) jika A = {x | x = 1, 3, 5, ...}
2. Fungsi Densitas Probabilitas untuk Variabel Random Kontinu
Misalkan Ωx adalah ruang dari variabel random kontinu X, maka fungsi f dari Ωx ke R dinamakan fungsi densitas probabilitas (FDP) dari variabel random X dengan simbol f(x) jika dipenuhi:
1. (∀x). f(x) ≥ 0
Nilai fungsi tak pernah negatif.
2. Integral menyeluruh adalah 1
1. Peluang interval
Diketahui variabel random X dengan Fdp f(x) yang didefinisikan sbb.
untuk P(1 < X < 3):
3. Fungsi Distribusi Kumulatif
Fungsi Distribusi Kumulatif dari variabel random X yang dinotasikan dengan F(x) adalah fungsi dengan domain R = {x | −∞ < x < ∞} dan range {F(x) | 0 ≤ F(x) ≤ 1} didefiniskan sebagai:
F(x) = P(X ≤ x).
Syarat-syarat fungsi distribusi kumulatif:
1. F(−∞) = 0 dan F(∞) = 1
2. Nilai F(x) tidak pernah turun, artinya nilai f(x) konstan atau naik.
(∀a, b ∈ R). a < b → F(a) ≤ F(b)
(∀a, b ∈ R). a < b → F(a) ≤ F(b)
3. Nilai F(x) kontinu kanan, artinya limit kanan dari F(x) sama dengan nilai F(x)
Jika X adalah variabel random, maka F(x) dapat diperoleh dari f(x) dan sebaliknya.
a. Untuk X diskrit:
Contoh:
b. Untuk X kontinu:Diberikan VR X dengan f(x) didefinisikan sebagai berikut:








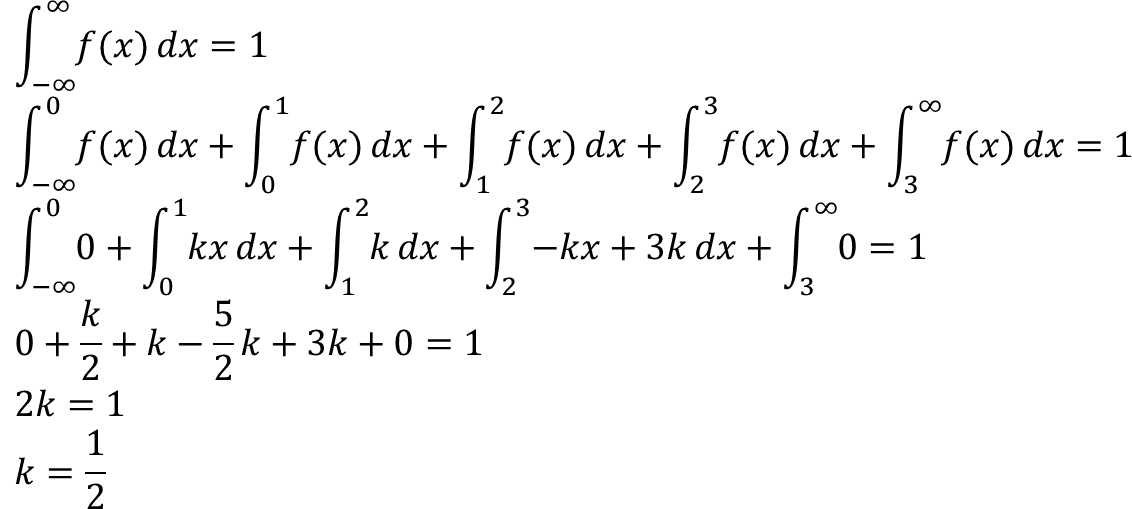
















Komentar
Posting Komentar