Grafik Fungsi Trigonometri

1. Grafik Fungsi Trigonometri Dasar

A. Grafik Fungsi Sinus Dasar

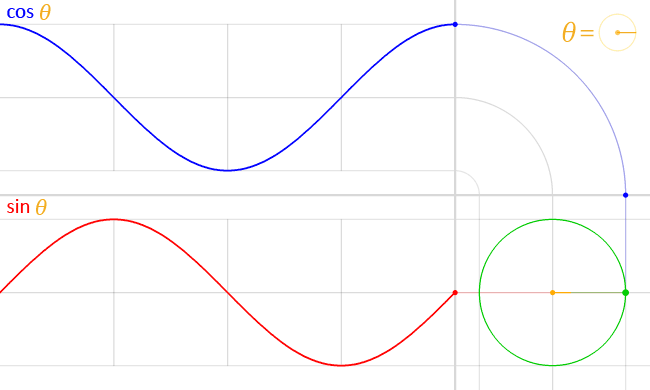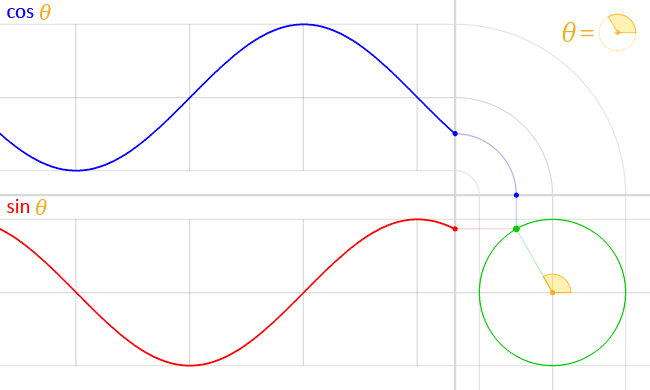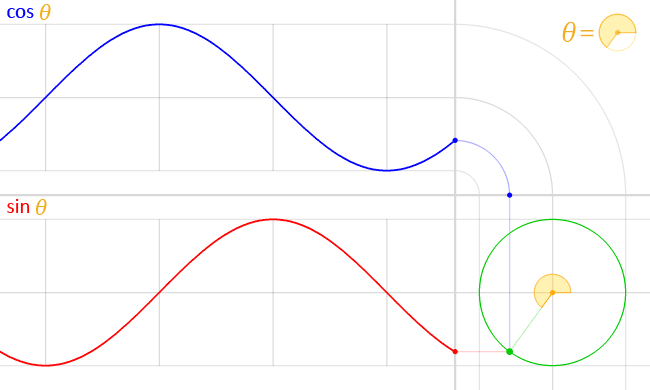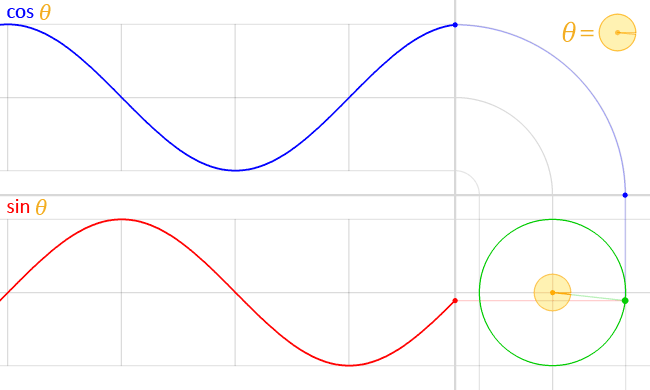
Misal diberikan fungsi trigonometri y = sin(t), grafiknya adalah:

keterangan:

• Memotong sumbu y di O(0, 0) dan memotong sumbu x di (kπ, 0), ∀k ∈ Z

• Periodenya (panjang gelombang) adalah 2π

• Amplitudonya adalah 1

• Nilai maksimum adalah 1 dan nilai minimum adalah –1

dengan nilai maksimum tercapai di x = ½π dan nilai minimum tercapai di x = 3π/2

B. Grafik Fungsi Kosinus Dasar

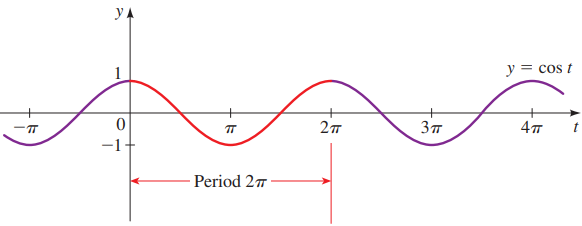
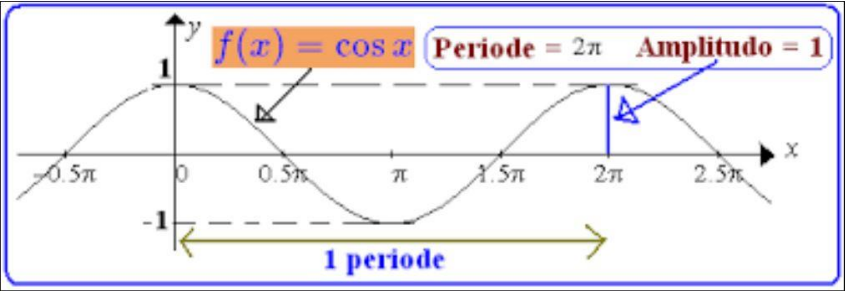
Misal diberikan fungsi trigonometri y = cos(t), grafiknya adalah:

keterangan:

• Memotong sumbu y di (0, 1) dan memotong sumbu x di ((k + ½)π, 0), ∀k ∈ Z

• Periodenya (panjang gelombang) adalah 2π

• Amplitudonya adalah 1

• Nilai maksimum adalah 1 dan nilai minimum adalah –1

dengan nilai maksimum tercapai di x = 0 dan nilai minimum tercapai di x = π

C. Grafik Fungsi Tangen Dasar

Misal diberikan fungsi trigonometri y = tan(x), grafiknya adalah:

• Memotong sumbu y di O(0, 0) dan memotong sumbu x di (kπ, 0), ∀k ∈ Z

• Periodenya (panjang gelombang) adalah π

• Memiliki asimtot tegak di x = k + ½π; ∀k ∈ Z

• Grafiknya monoton naik

D. Grafik Fungsi Kotangen Dasar

Misal diberikan fungsi trigonometri y = cot(x), grafiknya adalah:

• Tidak memotong sumbu y dan memotong sumbu x di ((k + ½)π, 0), ∀k ∈ Z

• Periodenya (panjang gelombang) adalah π

• Memiliki asimtot tegak di x = kπ; ∀k ∈ Z

• Grafiknya monoton turun

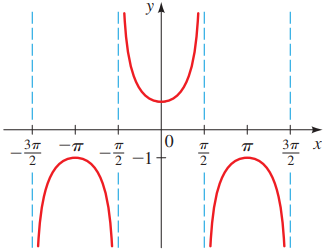
E. Grafik Fungsi Sekan Dasar

Misal diberikan fungsi trigonometri y = sec(x), grafiknya adalah:

• Memotong sumbu y di (0, 1) dan tidak memotong sumbu x

• Periodenya (panjang gelombang) adalah 2π

• Memiliki asimtot tegak di x = (k + ½)π; ∀k ∈ Z

• Memiliki nilai minimum lokal dan maksimum lokal.

Nilai minimum lokal tercapai di titik-titik (2kπ, 1); ∀k ∈ Z

Nilai maksimum lokal tercapai di titik-titik ((2k + 1)π, –1); ∀k ∈ Z

F. Grafik Fungsi Kosekan Dasar

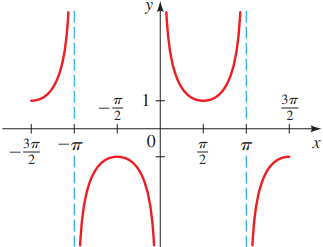
Misal diberikan fungsi trigonometri y = csc(x), grafiknya adalah:

• Tidak memotong sumbu x maupun sumbu y

• Periodenya (panjang gelombang) adalah 2π

• Memiliki asimtot tegak di x = kπ; ∀k ∈ Z

• Memiliki nilai minimum lokal dan maksimum lokal.

Nilai minimum lokal tercapai di titik-titik ((2k + ½)π, 1); ∀k ∈ Z

Nilai maksimum lokal tercapai di titik-titik ((2k – ½)π, –1); ∀k ∈ Z

2. Transformasi Fungsi

A. Pergeseran (Shifting), c > 0

y = f(x) + c dengan menggeser y = f(x) sejauh c satuan ke atas

y = f(x) – c dengan menggeser y = f(x) sejauh c satuan ke bawah

y = f(x – c) dengan menggeser y = f(x) sejauh c satuan ke kanan

y = f(x + c) dengan menggeser y = f(x) sejauh c satuan ke kiri

B. Peregangan (Stretching) dan pemampatan (Shrinking)

y = k.f(x) dengan meregangkan atau memampatkan y = f(x) secara tegak dengan faktor k

Peregangan dan pemampatan secara tegak berpengaruh pada amplitudo.

y = f(k.x) dengan meregangkan atau memampatkan y = f(x) secara mendatar dengan faktor k

Peregangan dan pemampatan secara mendatar berpengaruh pada periode.

C. Pencerminan (Reflection)

y = –f(x) dengan mencerminkan grafik y = f(x) terhadap sumbu x

y = f(–x) dengan mencerminkan grafik y = f(x) terhadap sumbu y

D. Bentuk Umum

Suatu fungsi trigonometri bisa mengalami transformasi, bentuk umumnya adalah:

y – c = k.f[a(x – b)] ↔ y = k.f[a(x – b)] + c

Contoh:

Gambar grafik fungsi y = 3.sin[2(x – π/4)] + 3

k = 3, a = 2, b = π/4, c = 3

• k = 3, berarti grafik diregangkan secara tegak dengan faktor 3, sehingga amplitudonya adalah |3| = 3

• a = 2, berarti grafik dimampatkan secara mendatar dengan faktor 2, sehingga periodenya adalah 2π/|2| = π

• b = π/4, berarti grafik digeser ke kanan sejauh π/4 satuan

• c = 3, berarti grafik digeser ke atas sejauh 3 satuan

• Memotong sumbu y di (0, c) = (0, 3) dan memotong sumbu x di ((k + ¼)π, 0), ∀k ∈ Z

• Nilai maksimum adalah c + |k| = 6 dan nilai minimum adalah c – |k| = 0

3. Menggambar Grafik Fungsi Trigonometri

Fungsi trigonometri sederhana dapat digambarkan dengan mudah, hanya bermodalkan grafik fungsi trigonometri dasar dan transformasi fungsi. Akan tetapi, untuk fungsi trigonometri yang lebih rumit, tentunya kedua modal tersebut belum mencukupi. Berikut langkah-langkah menggambar grafik fungsi trigonometri:

1. Tentukan titik potong sumbu x dan sumbu y

2. Tentukan asimtot tegak (jika ada)

Catatan: Karena fungsi trigonometri bersifat periodik, tidak ada asimtot mendatar.

3. Tentukan nilai ekstrim fungsi, baik minimum maupun maksimum, lokal maupun global

4. Buat titik bantu (jika diperlukan), lalu hubungkan

Contoh:

1. Gambarkan grafik fungsi y = [5.cos(x) + 3]/[4.cos(x) – 2] pada interval [0, 2π]

• Titik potong sumbu x adalah ketika pembilang nol dan penyebut taknol

5.cos(x) + 3 = 0

cos(x) = –⅗

x = ±2,2143 + 2kπ (dalam radian)

x = 2,2143; 4,0689

titik potong sumbu x adalah (2,2143; 0) dan (4,0689; 0)

• Titik potong sumbu y

y = f(0) = [5 + 3]/[4 – 2] = 4

titik potong sumbu y adalah (0, 4)

• Asimtot tegak

asimtot tegak ketika pembilang taknol dan penyebut nol

4.cos(x) – 2 = 0

cos(x) = ½

x = ±π/3 + 2kπ

x = π/3; 5π/3

• Nilai ekstrim

Misal [5.cos(x) + 3]/[4.cos(x) – 2] = k

5.cos(x) + 3 = k[4.cos(x) – 2] = 4k.cos(x) – 2k

(5 – 4k).cos(x) = –2k – 3

cos(x) = (–2k – 3)/(5 – 4k)

Untuk cos(x) = 1:

(–2k – 3)/(5 – 4k) = 1

–2k – 3 = 5 – 4k

–2k + 4k = 2k = 5 + 3 = 8

k = 8/2 = 4

tercapai pada x = 0; 2π

(0, 4), (2π, 4)

Untuk cos(x) = –1:

(–2k – 3)/(5 – 4k) = –1

–2k – 3 = 4k – 5

4k + 2k = 6k = –3 + 5 = 2

k = 2/6 = ⅓

tercapai pada x = π

(π, ⅓)

• Titik bantu

x = π/6 → y = [5.cos(π/6) + 3]/[4.cos(π/6) – 2] = (11√3 + 21)/8

x = 7π/4 → y = [5.cos(7π/4) + 3]/[4.cos(7π/4) – 2] = (11√2 + 16)/4

2. Gambarkan grafik fungsi y = 3.cos(x) + 4.sin(x) + 1

• Titik potong sumbu x

y = 3.cos(x) + 4.sin(x) + 1 = 0

3.cos(x) + 4.sin(x) = –1

misal tan(α) = 4/3 → α = 0,9273 ∨ α = 4,0689

cos(α) = 3/5 → α = 0,9273 ∨ α = 5,3559

sehingga α = 0,9273

cos(x – α) = –1/5

x – α = ±1,772 + 2kπ

x = 2,6994 ∨ x = 5,4383

titik potong sumbu x adalah (2,6994; 0) dan (5,4383; 0)

• Titik potong sumbu y

y = f(0) = 3.cos(0) + 4.sin(0) + 1 = 4

titik potong sumbu y adalah (0, 4)

• Tidak ada asimtot karena fungsi tersebut tidak ada pembagian dan hanya ada sinus dan kosinus.

• Nilai ekstrim

Nilai maksimum dari a.cos(x) + b.sin(x) adalah √(a² + b²) = √(3² + 4²) = 5 dan nilai minimumnya adalah –√(a² + b²) = –5

sehingga nilai maksimum adalah 5 + 1 = 6 dan nilai minimumnya adalah –5 + 1 = –4

Nilai maksimum tercapai di cos(x – α) = 1 = cos(0)

x – α = 0

x = α = 0,9273

Titik maksimumnya adalah (0,9273; 6)

Nilai minimum tercapai di cos(x – α) = –1 = cos(π)

x – α = π

x = π + α = 4,0689

Titik minimumnya adalah (4,0689; –4)

3. Gambarkan grafik fungsi y = 2.cos(x).cos(x – π/3)

• Titik potong sumbu x

y = 2.cos(x).cos(x – π/3) = 0

cos(x) = 0 ∨ cos(x – π/3) = 0

x = π/2, 3π/2 ∨ x = 5π/6, 11π/6

titik potong sumbu x adalah (π/2, 0), (5π/6, 0), (3π/2, 0), (11π/6, 0)

• Titik potong sumbu y

y = f(0) = 2.cos(0).cos(–π/3) = 2.1.½ = 1

titik potong sumbu y adalah (0, 1)

• Nilai minimum dan maksimum

y = 2.cos(x).cos(x – π/3) = cos(π/3) + cos(2x – π/3) = ½ + cos(2x – π/3)

sehingga nilai minimum adalah ½ – 1 = –½

tercapai di cos(2x – π/3) = –1 = cos(π)

2x – π/3 = (2k + 1)π

x – π/6 = (k + ½)π

x = 2π/3; 5π/3

titik minimum adalah (2π/3, –½) dan (5π/3, –½)

nilai maksimum adalah ½ + 1 = 3/2

tercapai di cos(2x – π/3) = 1 = cos(0)

2x – π/3 = 2kπ

x – π/6 = kπ

x = π/6; 7π/6

titik minimum adalah (π/6, 3/2) dan (7π/6, 3/2)