Integral Lipat Tiga di Koordinat Tabung dan Bola
1. Integral Lipat Tiga di Koordinat Tabung / Silindrik
Koordinat silinder dan Cartesius dihubungkan oleh persamaan:
x = r.cos(θ), y = r.sin(θ), x² + y² = r²
Akibatnya, fungsi f(x, y, z) berubah menjadi:
f(x, y, z) = f(r.cos(θ), r.sin(θ), z) = F(r, θ, z)
ketika ditulis dalam koordinat silinder.
Misalkan sekarang kita ingin menghitung integral di suatu benda pejal S. Pertimbangkan untuk membagi S dengan menggunakan grid silinder, di mana elemen volume yang tipikal. Bagian ini yang disebut irisan silinder memiliki volumenya, ingat kembali bahwa luas alasnya berdasarkan koordinat polar adalah
ΔAₖ = r̅ₖ Δrₖ Δθₖ, sehingga volumenya
ΔVₖ = r̅ₖ Δrₖ Δθₖ Δzₖ, maka jumlah yang mendekati integral tersebut memiliki bentuk:
Dengan mengambil limit ketika norma partisi mendekati nol, kita mendapatkan integral baru dan menyarankan sebuah rumus penting untuk mengubah dari koordinat Cartesius ke koordinat silinder dalam integral rangkap tiga.
Misalkan S adalah suatu benda pejal yang sederhana terhadap z dan proyeksi S di bidang XOY, yaitu Sxy, adalah sederhana terhadap r. Jika f kontinu pada S, maka
Hal yang perlu diperhatikan adalah dz dy dx dalam koordinat Cartesius menjadi r dz dr dθ dalam koordinat silinder.
Contoh:
Tentukan volume dari benda pejal S di oktan pertama yang dibatasi di atas oleh paraboloid z = 4 – x² –y², dan secara lateral oleh silinder x² + y² = 2x.
Dalam koordinat silinder, paraboloidnya adalah z = 4 – r² dan silindernya adalah r = 2 cos θ. Variabel z bergerak dari bidang XOY sampai ke paraboloid, yaitu dari 0 sampai 4 – r². Untuk θ tertentu, r bergerak dari 0 sampai 2 cos θ. Terakhir, θ bergerak dari 0 sampai π/2. Dengan demikian,
Ingat kembali bahwa persamaan
x = ρ.sin(φ).cos(θ), y = ρ.sin(φ).sin(θ), z = ρ.cos(φ)
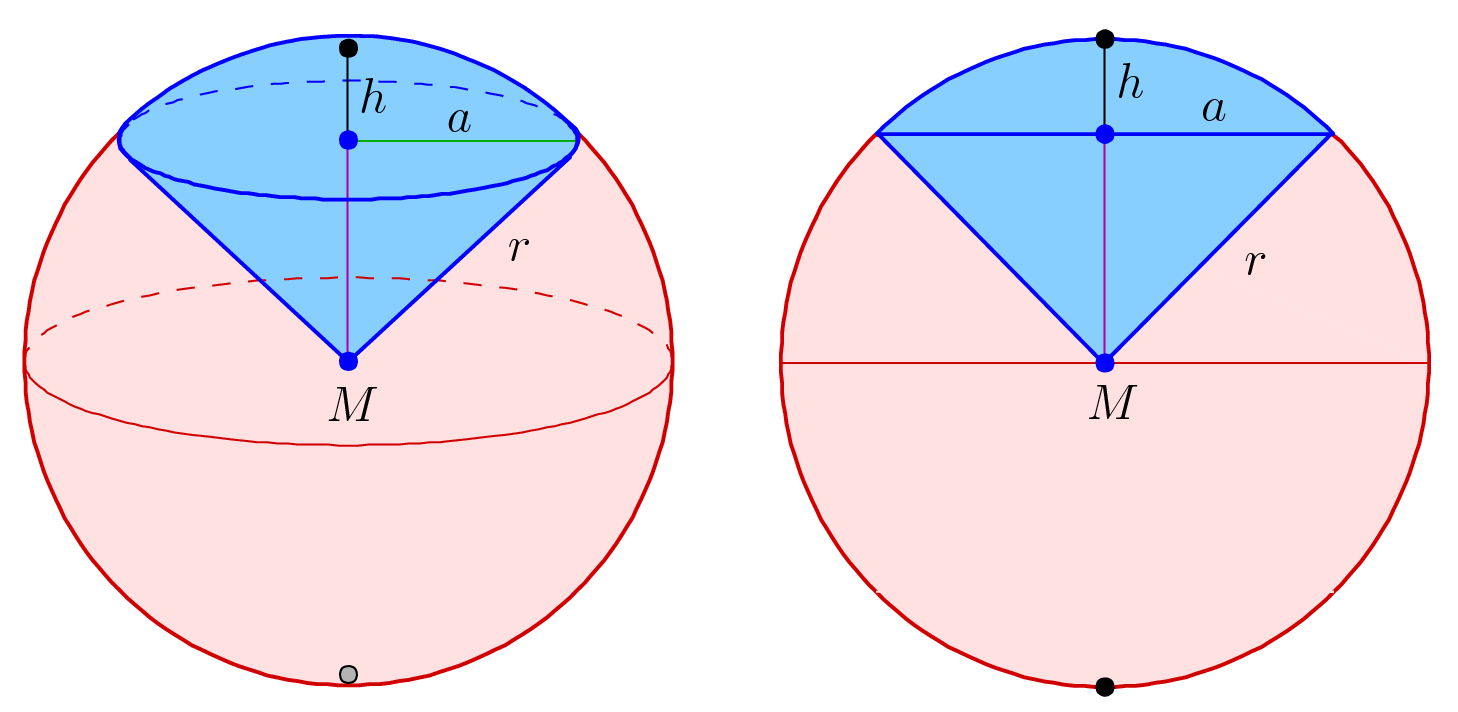
menghubungkan koordinat bola dan koordinat Cartesius. Elemen volume dalam koordinat bola (disebut potongan bola). Untuk menunjukkan volume potongan bola secara tiga dimensi, ingat kembali juring bola, dimana volumenya adalah ⅔.𝜋.ρ².h = ⅔.𝜋.ρ².ρ[1 – cos(φ)] = ⅔.𝜋.ρ³.[1 – cos(φ)].
Misal kita memberi batas sudut tegaknya oleh φ = 𝛾 dan φ = 𝛿, selisih volume juringnya adalah;
⅔.𝜋.ρ³.[1 – cos(𝛿)] – ⅔.𝜋.ρ³.[1 – cos(𝛾)] = ⅔.𝜋.ρ³.[cos(𝛾) – cos(𝛿)] = –⅔.𝜋.ρ³.2.sin[(𝛾 + 𝛿)/2].sin[(𝛾 – 𝛿)/2] = (4/3).𝜋.ρ³.sin(φ̄).sin[(𝛿 – 𝛾)/2] = (4/3).𝜋.ρ³.sin(φ̄).sin(½Δφ)
Lalu ambil potongan mendatar yang dibatasi oleh θ = 𝛼 dan θ = 𝛽, dari volume selisih juring tadi, volume potongan ini adalah (𝛽 – 𝛼)/2𝜋 × (4/3).𝜋.ρ³.sin(φ̄).sin(½Δφ) = ⅔.ρ³.sin(φ̄).sin(½Δφ).Δθ.
Selanjutnya ambil potongan berlapis dibatasi oleh ρ = a dan ρ = b, selisih volumenya adalah:
⅔.(b³ – a³).sin(φ̄).sin(½Δφ).Δθ = ⅔.(b – a).(b² + ab + a²).sin(φ̄).sin(½Δφ).Δθ = ⅔.Δρ.(b² + ab + a²).sin(φ̄).sin(½Δφ).Δθ.
Jadi, volume potongan bola dibatasi oleh ρ = a dan ρ = b secara berlapis, θ = 𝛼 dan θ = 𝛽 secara mendatar, φ = 𝛾 dan φ = 𝛿 secara tegak adalah ⅔.Δρ.(b² + ab + a²).sin(φ̄).sin(½Δφ).Δθ.
Misal kita ambil potongan yang sangat kecil, kita limitkan Δρ, Δθ, Δφ menuju 0, akan membuat:
∆𝜌 → 0, sehingga 𝑎 → 𝜌 ̅ dan 𝑏 → 𝜌 ̅, sehingga b² + ab + a² → 3𝜌 ̅²
Δφ → 0, sehingga sin(½Δφ) → ½Δφ (Ingat kembali limit trigonometri)
ΔV ≈ ⅔.Δρ.3𝜌 ̅².sin(φ̄).½.Δφ.Δθ = 𝜌 ̅².sin(φ̄).Δρ.Δθ.Δφ
di mana (𝜌 ̅, φ̄, θ̄) adalah titik yang dipilih secara tepat dalam irisan.
Dengan membagi benda padat S menggunakan grid bola, membentuk jumlah yang sesuai, dan mengambil limit, kita mendapatkan integral berulang di mana dz dy dx digantikan oleh ρ² sin φ dρ dθ dφ.
Misal f(x, y, z) = f[ρ.sin(φ).cos(θ), ρ.sin(φ).sin(θ), ρ.cos(φ)] = F(ρ, θ, φ)
Contoh:
Tentukan pusat massa dari hemisfer pejal berdensitas 1 yang alasnya berpusat di O(0, 0, 0) dan jari-jarinya r.
Tentukan pusat massa dari hemisfer pejal berdensitas 1 yang alasnya berpusat di O(0, 0, 0) dan jari-jarinya r.
Karena simetris terhadap bidang XOZ dan YOZ, x̄ = 0 dan ȳ = 0, adapun z̄ kita gunakan rumus pusat massa.
Karena densitasnya 1, massa dari hemisfer sama dengan volumenya, yaitu ⅔.𝜋.r³, sedangkan momen terhadap bidang XOY adalah:



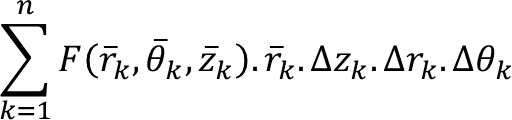







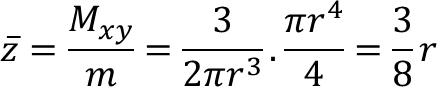


Komentar
Posting Komentar