Persamaan Diferensial Muqodimah
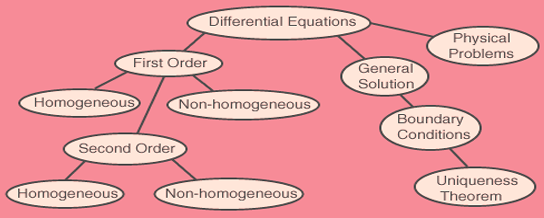
1. Persamaan Diferensial
Persamaan diferensial adalah suatu persamaan yang menyatakan hubungan fungsi yang tidak di ketahui dan turunan-turunannya.
Misalkan f(x) mendefinisikan sebuah fungsi dari x pada suatu interval I[a, b] dimana a ≤ x ≤ b. Persamaan diferensial adalah persamaan yang memuat derivatif dari f(x).
Orde dari suatu persamaan diferensial adalah orde tertinggi derivatif yang termuat dalam persamaan itu.
2. Penyelesaian Persamaan Diferensial
Penyelesaian suatu persamaan diferensial ialah mencari suatu fungsi yang tidak memuat turunan dan memenuhi persamaan diferensial yang diberikan. Penyelesaian dapat saja dilakukan satu atau beberapa kali integrasi.
3. Persaman Diferensial Biasa dan Parsial
Jika hanya ada satu variabel bebas, maka disebut Persamaan Diferensial Biasa (PDB). Sedangkan jika persamaan memuat dua atau lebih peubah bebas, maka disebut Persamaan Diferensial Parsial (PDP).
4. Masalah Nilai Awal
Misalkan kita akan mencari penyelesaian dari y = y(x) dari PDB orde satu y' = f(x, y) yang memenuhi
y(x₀) = y₀.
Contoh:
dy/dx = 2xy; y(1) = 2


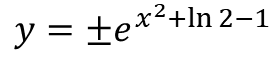


Komentar
Posting Komentar