Persamaan Diferensial Separabel
Untuk Persamaan Diferensial Separabel orde satu yang berbentuk y′ = f(x), dimana f fungsi kontinu dari satu variabel bebas x, maka kita dapat mengintegralkan secara langsung kedua ruas untuk memperoleh penyelesainnya.
Bentuk umum:
dy/dx = f(x, y)
Untuk mencari penyelesaian umum dari persamaan diferensial separabel, terlebih dahulu kita pisahkan variabel x dan y, sehingga kita peroleh fungsi f(x, y) = p(x).q(y)
Contoh
1. (xy)dx + (1 + x²)dy = 0
(1 + x²)dy = (−xy)dx
Misal u = 1 + x²; du = 2x dx; −½du = −x dx
eksponenkan kedua ruas
2. Bentuk ini juga merupakan Perdif separabel, coba faktorkan masing-masing pembilang dan penyebut.
eksponenkan kedua ruas
2. Bentuk ini juga merupakan Perdif separabel, coba faktorkan masing-masing pembilang dan penyebut.
v = 1 − x² → dv = −2x dx ↔ −½dv = x dx
y − 4⋅ln|4 + y| + ½⋅ln|1 − x²| = C₃
3. dy/dx = cot(x)⋅tan(y)
cot(y) dy = cot(x) dx
∫cot(y) dy = ∫cot(x) dx
ln|sin(y)| + C₁ = ln|sin(x)| + C₂
ln|sin(y)| = ln|sin(x)| + C₃, eksponensialkan masing-masing ruas
|sin(y)| = eC₃⋅|sin(x)| = C₄⋅|sin(x)|
sin(y) = ±C₄⋅|sin(x)|
y = sin⁻¹(±C₄⋅|sin(x)|)
4. (x) dy/dx + 2y² = 2
dy/dx = (2 − 2y²)/x
Integralkan ruas kiri
¼⋅ln|1 + y| + ¼⋅ln|1 − y| + C₁ = ln|x| + C₂, kalikan masing-masing ruas dengan 4
¼⋅ln|1 + y| + ¼⋅ln|1 − y| + C₁ = ln|x| + C₂, kalikan masing-masing ruas dengan 4
ln|1 − y²| = 4⋅ln|x| + C₃, eksponensialkan masing-masing ruas
|1 − y²| = eC₃⋅x⁴
1 − y² = ±C₄⋅x⁴
y² = 1 ± C₄⋅x⁴
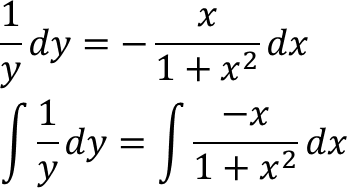




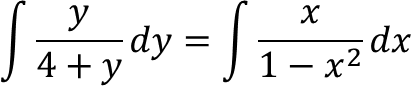


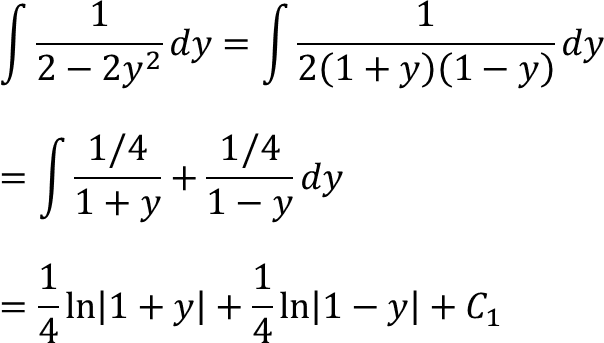


Komentar
Posting Komentar