Relasi Rekursif dengan Fungsi Pembangkit
Dalam banyak contoh, suku ke-n dalam relasi rekursif dapat diperoleh sebagai koefisien xⁿ dalam perluasan deret pangkat dari suatu fungsi g(x) yang dapat dianggap sebagai fungsi pembangkit untuk relasi rekursif yang diberikan. Cukup sering persamaan fungsional untuk g(x) dapat diselesaikan secara aljabar dan kemudian diperoleh dengan menyatakan g(x) sebagai deret pangkat. Dengan kata lain, relasi rekursif dapat diselesaikan dengan menggunakan fungsi pembangkit terkait.
Contoh Soal
1. Selesaikan persamaan rekursif
aₙ − 5aₙ₋₁ + 6aₙ₋₂ = 0 untuk n ≥ 2; dengan a₀ = 2; a₁ = 5
solusi:
Misalkan fungsi pembangkit biasa dari barisan tersebut adalah
Kalikan persamaan rekursif dengan xⁿ
aₙxⁿ − 5aₙ₋₁xⁿ + 6aₙ₋₂xⁿ = 0
Ambil jumlah untuk n ≥ 2 diperoleh
P(x) − 2 − 5x − 5x.P(x) + 10x + 6x².P(x) = 0
(1 − 5x + 6x²).P(x) = 2 − 5x
P(x) = (2 − 5x)/(1 − 5x + 6x²)
uraikan dengan fraksi parsial
2. Selesaikan persamaan rekursif
aₙ₊₁ − aₙ = 3ⁿ untuk n ≥ 0; dengan a₀ = 1
solusi:
Misalkan fungsi pembangkit biasa dari barisan tersebut adalah
Kalikan persamaan rekursif dengan xⁿ
aₙ₊₁xⁿ − aₙxⁿ = 3ⁿxⁿ
Ambil jumlah untuk n ≥ 0 diperoleh
(1/x − 1).P(x) − 1/x = 1/(1 − 3x)
[(1 − x)/x].P(x) = 1/(1 − 3x) + 1/x
3. Selesaikan persamaan rekursif
aₙ₊₁ − aₙ = n² untuk n ≥ 0; dengan a₀ = 1
solusi:
Misalkan fungsi pembangkit biasa dari barisan tersebut adalah
Kalikan persamaan rekursif dengan xⁿ
aₙ₊₁xⁿ − aₙxⁿ = n²xⁿ
Ambil jumlah untuk n ≥ 0 diperoleh
sedikit manipulasi
(1/x).[P(x) − 1] − P(x) = ∑n²
(1/x − 1).P(x) − 1/x = ∑n² + 1/x
[(1 − x)/x].P(x) = ∑n² + 1/x
mari kita uraikan ∑n² yang rumit ini, CALCULUS REQUIRED!
P(x) = (x³ + x²)/[(1 − x)⁴] + 1/(1 − x)
dan lagi-lagi kalkulus lagi


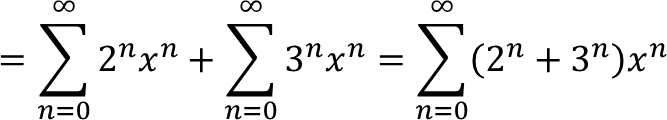




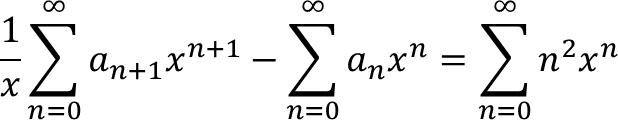
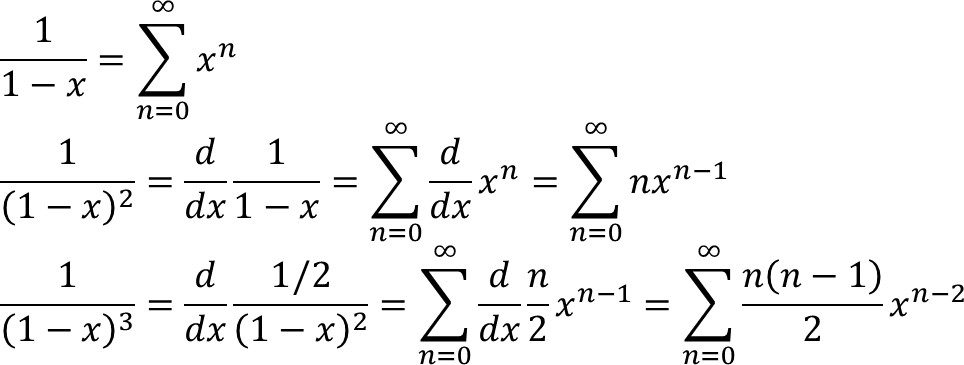



Komentar
Posting Komentar