Operasi Graf
1. Operasi Intragraf
A. Komplemen Graf (Complementary Graph)
Jika G graf sederhana maka komplemen graf G (disimbolkan G̅) mempunyai ciri:
➢ Himpunan titik G̅ sama dengan himpunan titik di G
➢ Dua titik u dan v di G̅ adjacent jika dan hanya jika dua titik u dan v tersebut tidak adjacent di G
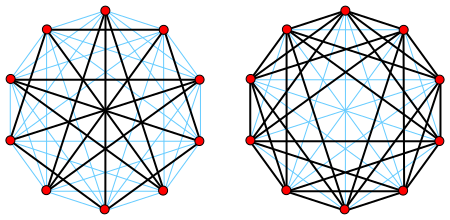
Sebagai contoh, perhatikan gambar berikut:
Pada gambar ini diberikan dua graf yang saling komplemen.B. Penghapusan Titik
Jika kita menghapus titik v dan semua sisi yang bersisian dengan v dari graf G = (V, E), kita menghasilkan graf bagian yang baru, yang dinotasikan dengan G − v. Perhatikan bahwa G − v = (V \ {v}, E'), dimana E' adalah himpunan dari sisi-sisi di G yang tidak bersisian dengan v.
Jika V' ⊆ V, kita dapat menghasilkan graf bagian dari G dengan menghapus titik-titik pada V' dari graf G. Graf yang dihasilkan memiliki himpunan titik V \ V' dan himpunan sisinya adalah E' dengan E' adalah himpunan dari sisi-sisi di G yang tidak bersisian dengan simpul pada V'.
Keterhubungan titik dari graf tidak lengkap G, disimbolkan v(G), adalah banyaknya minimum penghapusan titik (dan sisi yang incident dengan titik tersebut) yang mengakibatkan graf menjadi tidak terhubung.
C. Penghapusan Sisi
Diberikan graf G = (V, E) dan sisi e ∈ E, kita dapat menghasilkan graf bagian dari G dengan menghapus e. Graf bagian yang dihasilkan, ditulis dengan G − e, memiliki himpunan titik yang sama dengan V pada G dan himpunan sisi E\{e}. Sehingga G − e = (V, E\{e}).
Jika E′ ⊆ E, kita dapat menghasilkan graf bagian dari G dengan menghapus sisi-sisi pada E′ dari graf. Graf yang dihasilkan memiliki himpunan titik yang sama dengan V pada G. Himpunan sisinya adalah E \ E′.
Keterhubungan sisi dari graf G, disimbolkan e(G), adalah banyaknya minimum penghapusan sisi yang mengakibatkan graf menjadi tidak terhubung.
D. Penambahan Sisi
Kita juga dapat menambahkan suatu sisi e untuk menambahkan graf yang lebih besar jika sisi ini menghubungkan dua titik pada G. Kita notasikasikan G + e sebagai graf baru yang dihasilkan dengan menambahkan sisi baru e menghubungkan dua titik yang sebelumnya tidak bersisian pada graf G, sehingga G + e = (V, E ∪{e}).
E. Kontraksi sisi
Terkadang ketika kita membuang sisi dari suatu graf, kita tidak ingin meninggalkan titik ujung sebagai titik-titik yang terpisah pada graf bagian baru yang dihasilkan. Dalam kasus ini kita bisa melakukan kontraksi sisi dengan cara:
• menghapus sisi dengan titik ujung u dan v
• menggabungkan u dan v menjadi satu titik w
• setiap sisi dengan u dan v sebagai titik ujung diganti dengan sisi dengan w sebagai suatu titik ujung dan titik ujung yang keduanya tetap sama
Sehingga kontraksi sisi e dengan titik ujung u dan v pada graf G = (V, E) menghasilkan graf G' = (V', E'), yang bukan merupakan graf bagian dari G, dengan V' = V \ {u, v} ∪ {w} dan E' adalah sisi-sisi di E yang tidak memiliki u atau v sebagai titik ujung dan diganti dengan sisi yang menghubungkan w dengan setiap lingkungan dari u atau v di V.
2. Operasi Intergraf
A. Gabungan graf (graph union)
Gabungan dari graf G₁ = (V₁, E₁) dan G₂ = (V₂, E₂) adalah suatu graf dengan himpunan titik V₁ ∪ V₂ dan himpunan sisi E₁ ∪ E₂, dinotasikan dengan G₁ ∪ G₂.
B. Irisan graf (graph intersection)
Irisan dari graf G₁ = (V₁, E₁) dan G₂ = (V₂, E₂) adalah suatu graf dengan himpunan titik V₁ ∩ V₂ dan himpunan sisi E₁ ∩ E₂, dinotasikan dengan G₁ ∩ G₂.
C. Penjumlahan graf
Jumlah dari graf G₁ = (V₁, E₁) dan G₂ = (V₂, E₂) adalah suatu graf dengan himpunan titik V₁ ∪ V₂ dan himpunan sisi E₁ ∪ E₂, dinotasikan dengan G₁ ∪ G₂ ∪ {uv: u ∈ V₁, v ∈ V₂}.
D. Sisir graf (comb graph)
G dan H adalah Graf terhubung dan u adalah sebuah titik pada graf H, Operasi comb dari graf G dan graf H (disimbolkan G ▹ H) didefinisikan sebagai graf yang diperoleh dengan mengambil sebuah duplikasi dari graf G dan duplikasi dari graf H sebanyak ∣V(G)∣, yaitu Hᵢ dengan i = 1, 2, 3, ..., ∣V(G)∣, dan melekatkan titik u dari masing-masing graf Hᵢ pada titik ke-i dari graf G.
E. Corona graf
Operasi corona dari graf G dan graf H (disimbolkan G ⊙ H) didefinisikan sebagai graf yang diperoleh dengan mengambil sebuah duplikasi dari graf G dan duplikasi dari graf H sebanyak ∣V(G)∣, yaitu Hᵢ dengan i = 1, 2, 3, ..., ∣V(G)∣, kemudian menghubungkan setiap titik ke-i dari G ke setiap titik di Hᵢ.
F. Perkalian Kartesius
Dalam teori graf, hasil kali Kartesius dari graf G dan H yang disimbolkan dengan G × H adalah graf sedemikian rupa sehingga:
◘ Himpunan titik G × H adalah hasil kali Kartesius V(G) × V(H); dan
◘ Dua titik (u, v) dan (u', v') bertetangga di G × H jika dan hanya jika salah satu dari berikut ini
○ u = u' dan v bertetangga dengan v' di H, atau
○ v = v' dan u bertetangga dengan u' di G.








Komentar
Posting Komentar