Gerak Paksa / Forced Motion dan Fenomena Resonansi (Aplikasi Perdif)

1. Gerak Paksa (Forced Motion)

Sekarang kita pertimbangkan kasus khusus yang penting dari gerak paksa (forced motion). Artinya, kita tidak hanya mempertimbangkan efek redaman pada massa pada pegas, tetapi juga efek dari gaya eksternal periodik yang diterapkan F(t) = F₁·cos(ωt) untuk semua t ≥ 0, di mana F₁ dan ω adalah konstanta. Maka persamaan diferensial dasar menjadi:

mx'' + ax' + kx = F₁·cos(ωt).

Membagi dengan m dan menetapkan a/m = 2b, k/m = λ², dan F₁/m = E₁, ini mengambil bentuk yang lebih nyaman:

x'' + 2bx' + λ²x = E₁·cos(ωt).

Kita akan mengasumsikan bahwa konstanta redaman positif a cukup kecil sehingga redaman kurang dari kritis. Dengan kata lain, kita mengasumsikan bahwa b < λ. Oleh karena itu, fungsi komplementer dari persamaan diatas dapat ditulis:

Sekarang kita akan menemukan bagian partikuler dengan metode koefisien tak tentu. Kita misalkan:

xₚ = A·cos(ωt) + B·sin(ωt).

Maka:

xₚ' = –ωA·sin(ωt) + ωB·cos(ωt),

xₚ'' = –ω²A·cos(ωt) – ω²B·sin(ωt).

Sehingga kita dapatkan:

[–2bωA + (λ² – ω²)B]·sin(ωt) + [(λ² – ω²)A + 2bωB]·cos(ωt) = E₁ cos ωt.

Dengan demikian, kita memiliki dua persamaan berikut dari mana untuk menentukan A dan B:

–2bωA + (λ² – ω²)B = 0,

(λ² – ω²)A + 2bωB = E₁.

Menyelesaikan persamaan ini, kita dapatkan:

Kita dapatkan bagian partikuler dalam bentuk:

Sekarang kita ubah ini ke dalam bentuk "sudut fase" alternatif; kita tulis:

di mana:

Dengan demikian bagian partikuler muncul dalam bentuk:

di mana θ ditentukan. Jadi, solusi umumnya adalah:

Amati bahwa solusi ini adalah jumlah dari dua suku. Suku pertama,

merepresentasikan osilasi teredam yang akan menjadi seluruh gerakan sistem jika gaya eksternal F₁·cos(ωt) tidak ada. Suku kedua,

yang dihasilkan dari keberadaan gaya eksternal, merepresentasikan gerak harmonik sederhana dengan periode 2π/ω. Karena faktor peredam ce⁻ᵇᵗ, kontribusi dari suku pertama akan menjadi semakin kecil seiring berjalannya waktu dan akhirnya akan menjadi dapat diabaikan. Suku pertama ini karenanya disebut suku transien (transient term). Suku kedua, bagaimanapun, menjadi suku cosinus dari amplitudo konstan, terus berkontribusi pada gerakan secara periodik, dengan cara berosilasi. Akhirnya, suku transien telah menjadi relatif kecil, seluruh gerakan pada dasarnya akan terdiri dari yang diberikan oleh suku kedua ini. Suku kedua ini karenanya disebut suku tunak (steady-state term).

2. Fenomena Resonansi

Sekarang kita mempertimbangkan amplitudo dari getaran keadaan tunak yang dihasilkan dari gaya eksternal periodik yang didefinisikan untuk semua t oleh F(t) = F₁·cos(ωt), dimana kita mengasumsikan bahwa F₁ > 0. Untuk b, λ, dan E₁ yang tetap, kita lihat bahwa ini adalah fungsi f dari ω yang didefinisikan oleh

Jika ω = 0, gaya F(t) adalah konstan F₁ dan amplitudo f(ω) memiliki nilai E₁/λ² > 0. Juga, saat ω → ∞, kita lihat bahwa f(ω) → 0. Mari kita pertimbangkan fungsi f untuk 0 < ω < ∞. Menghitung turunan f′(ω) kita menemukan bahwa turunan ini sama dengan nol hanya jika

4ω[2b² – (λ² – ω²)] = 0

dan karenanya hanya jika ω = 0 atau ω = √(λ² – 2b²). Jika λ² < 2b², maka √(λ² – 2b²) adalah bilangan kompleks. Maka dalam kasus ini f tidak memiliki ekstremum untuk 0 < ω < ∞, melainkan f menurun secara monoton untuk 0 < ω < ∞ dari nilai E₁/λ² pada ω = 0 dan mendekati nol saat ω → ∞. Mari kita asumsikan bahwa λ² > 2b². Maka fungsi f memiliki maksimum relatif pada ω₁ = √(λ² – 2b²), dan nilai maksimum ini diberikan oleh

Ketika frekuensi dari fungsi gaya F₁·cos(ωt) sedemikian rupa sehingga ω = ω₁, maka fungsi gaya dikatakan berada dalam resonansi dengan sistem. Dengan kata lain, fungsi gaya yang didefinisikan oleh F₁·cos(ωt) berada dalam resonansi dengan sistem ketika ω mengasumsikan nilai ω₁ di mana f(ω) adalah maksimum. Nilai ω₁/(2π) disebut frekuensi resonansi dari sistem. Perhatikan baik-baik bahwa resonansi dapat terjadi hanya jika λ² > 2b². Maka karena λ² > 2b², redaman harus kurang kritis dalam kasus seperti itu.

Sekarang kita kembali ke notasi asli. Dalam hal kuantitas m, a, k, dan F₁ dari persamaan itu, fungsi f diberikan oleh

Dalam notasi asli ini frekuensi resonansi adalah

Karena frekuensi dari osilasi bebas teredam yang sesuai adalah

kita melihat bahwa frekuensi resonansi lebih kecil daripada frekuensi osilasi bebas teredam yang sesuai.

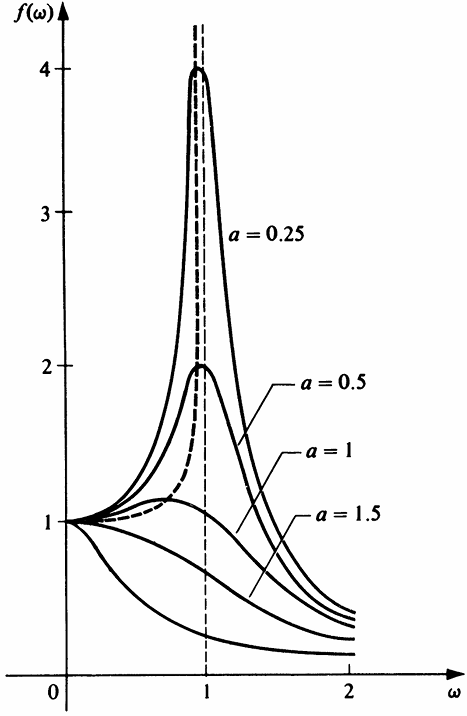
Grafik f(ω) disebut kurva resonansi dari sistem. Untuk sistem tertentu dengan m, k, dan F₁ yang tetap, ada kurva resonansi yang sesuai dengan setiap nilai koefisien redaman a ≥ 0. Mari kita pilih m = k = F₁ = 1, misalnya, dan gambarkan kurva resonansi yang sesuai dengan nilai a tertentu yang dipilih. Dalam kasus ini kita memiliki

dan frekuensi resonansi diberikan oleh

Grafik-grafik tersebut muncul pada gambar berikut:

Amati bahwa resonansi terjadi dalam kasus ini hanya jika a < √2. Saat a menurun dari √2 ke 0, nilai ω₁ di mana resonansi terjadi meningkat dari 0 ke 1 dan nilai maksimum f(ω) yang sesuai menjadi semakin besar. Dalam kasus batas a = 0, maksimum telah menghilang dan diskontinuitas tak terbatas terjadi pada ω = 1. Dalam kasus ini solusi kita benar-benar rusak, karena kemudian

dan f(1) tidak terdefinisi. Kasus batas ini adalah contoh resonansi tak teredam, sebuah fenomena yang akan kita selidiki sekarang.

Resonansi tak teredam terjadi ketika tidak ada redaman dan frekuensi gaya yang diterapkan sama dengan frekuensi alami sistem. Karena dalam kasus ini a = 0 dan frekuensi ω/(2π) sama dengan frekuensi alami

persamaan diferensial direduksi menjadi

atau

di mana E₁ = F₁/m. Karena fungsi homogennya adalah

kita tidak dapat mengasumsikan solusi partikuler dalam bentuk

Sebaiknya kita harus mengasumsikan

Mendiferensiasikan ini dua kali dan mensubstitusikannya ke dalam persamaan awal, kita menemukan bahwa

Jadi solusi partikular yang dihasilkan dari fungsi gaya

diberikan oleh

Mengekspresikan fungsi homogen dalam bentuk “fase-sudut” yang setara, kita lihat bahwa solusi umumnya diberikan oleh

Gerakan yang didefinisikan adalah jumlah dari suku periodik dan suku osilasi yang amplitudonya

meningkat dengan t. Grafik fungsi yang didefinisikan oleh suku yang terakhir ini,

muncul pada gambar berikut:

Seiring t meningkat, suku ini jelas mendominasi seluruh gerakan. Seseorang mungkin berpendapat bahwa saat t → ∞, osilasi akan menjadi tak terbatas. Namun, akal sehat mengintervensi dan meyakinkan kita bahwa sebelum fenomena menarik ini dapat terjadi, sistem akan rusak dan kemudian tidak akan lagi berlaku.

Contoh Soal

1. Sebuah beban 6 lb dipasang di ujung bawah pegas koil yang digantung dari langit-langit, dengan konstanta pegas 27 lb/ft. Beban tersebut berhenti pada posisi kesetimbangannya, dan dimulai pada t = 0 sebuah gaya eksternal yang diberikan oleh F(t) = 12·cos(20t) diterapkan pada sistem. Tentukan perpindahan yang dihasilkan sebagai fungsi waktu, dengan asumsi redaman dapat diabaikan.

• Solusi homogen

Diberikan W = 6 lb, asumsikan g = 32 ft/s, diperoleh m = W/g = 6/32 = 3/16 slug.

Diberikan k = 27 lb/ft, diperoleh persamaan

(3/16)x'' + 27x = 12·cos(20t), kalikan masing-masing ruas dengan 16/3

x'' + 144x = 64·cos(20t)

Solusi homogen dapat ditentukan menggunakan persamaan karakteristik

r² + 144 = 0

r = ±12i, diperoleh solusi homogen

xₕ = c₁·cos(12t) + c₂·sin(12t).

• Solusi khusus

Diberikan F(t) = 12·cos(20t), sehingga solusi khususnya berbentuk xₚ = A·cos(20t) + B·sin(20t)

turunkan dua kali

xₚ' = –20A·sin(20t) + 20B·cos(20t)

xₚ'' = –400A·cos(20t) – 400B·sin(20t), masukkan ke persamaan awal

–400A·cos(20t) – 400B·sin(20t) + 144[A·cos(20t) + B·sin(20t)] = 64·cos(20t)

–256A·cos(20t) – 256B·sin(20t) = 64·cos(20t)

A = –¼ dan B = 0, jadi solusi khususnya adalah xₚ = –¼·cos(20t)

Solusi totalnya adalah

x = xₕ + xₚ = c₁·cos(12t) + c₂·sin(12t) – ¼·cos(20t), turunkan terhadap t

x' = –12c₁·sin(12t) + 12c₂·cos(12t) + 5·sin(20t)

Diberikan beban berhenti di posisi kesetimbangan, jadi x(0) = 0; juga beban dilepaskan dari keadaan diam, jadi x'(0) = 0; masukkan ke x dan x'

c₁·cos(0) + c₂·sin(0) – ¼·cos(0) = 0 ⇔ c₁ = ¼

–12c₁·sin(0) + 12c₂·cos(0) + 5·sin(0) = 0 ⇔ c₂ = 0

Jadi, perpindahannya adalah x = ¼·cos(12t) – ¼·cos(20t).

2. Sebuah beban 10-lb digantung di ujung bawah pegas koil yang digantung dari langit-langit, konstanta pegasnya adalah 20 lb/ft. Beban tersebut berhenti di posisi kesetimbangannya, dan dimulai pada t = 0 sebuah gaya eksternal yang diberikan oleh F(t) = 10·cos(8t) diterapkan pada sistem. Medium menawarkan hambatan dalam pound secara numerik sama dengan 5(dx/dt), di mana dx/dt adalah kecepatan sesaat dalam ft/s. Tentukan perpindahan beban sebagai fungsi waktu.

• Solusi homogen

Diberikan W = 10-lb, asumsikan g = 32 ft/s², diperoleh m = W/g = 10/32 = 5/16 slug.

Diberikan k = 20 lb/ft

Diberikan koefisien redaman oleh hambatan medium sebesar a = 5 lb·s/ft

Berdasarkan informasi awal, diperoleh persamaan diferensial

(5/16)x'' + 5x' + 20x = 10·cos(8t), kalikan masing-masing ruas dengan 16/5

x'' + 16x' + 64x = 32·cos(8t)

Solusi homogen dapat ditentukan menggunakan persamaan karakteristik

r² + 16r + 64 = 0

(r + 8)² = 0

r = –8, diperoleh solusi homogen

xₕ = c₁·e⁻⁸ᵗ + c₂t·e⁻⁸ᵗ.

• Solusi partikuler

Diberikan F(t) = 10·cos(8t), sehingga solusi khususnya berbentuk xₚ = A·cos(8t) + B·sin(8t)

turunkan dua kali

xₚ' = –8A·sin(8t) + 8B·cos(8t)

xₚ'' = –64A·cos(8t) – 64B·sin(8t), masukkan ke persamaan awal

–64A·cos(8t) – 64B·sin(8t) + 16[–8A·sin(8t) + 8B·cos(8t)] + 64[A·cos(8t) + B·sin(8t)] = 10·cos(8t)

128B·cos(8t) – 128A·sin(8t) = 32·cos(8t)

B = 32/128 = ¼, dan A = 0, jadi solusi khususnya adalah xₚ = ¼·sin(8t)

Solusi totalnya adalah

x = xₕ + xₚ = c₁·e⁻⁸ᵗ + c₂t·e⁻⁸ᵗ + ¼·sin(8t), turunkan terhadap t

x' = –8c₁·e⁻⁸ᵗ + c₂·e⁻⁸ᵗ – 8c₂t·e⁻⁸ᵗ + 2·cos(8t)

Diberikan beban berhenti di posisi kesetimbangan, jadi x(0) = 0; juga beban dilepaskan dari keadaan diam, jadi x'(0) = 0; masukkan ke x dan x'

c₁ + 0 + ¼·sin(0) = 0 ⇔ c₁ = 0

–8c₁ + c₂ – 0 + 2·cos(0), masukkan c₁ = 0

c₂ = –2

Jadi, perpindahannya adalah x = –2t·e⁻⁸ᵗ + ¼·sin(8t)

3. Sebuah beban 6-lb digantung di ujung bawah pegas koil yang digantung dari langit-langit. Beban tersebut berhenti dalam posisi kesetimbangannya, sehingga meregangkan pegas 4 inci. Kemudian dimulai pada t = 0 sebuah gaya eksternal yang diberikan oleh F(t) = 27·sin(4t) − 3·cos(4t) diterapkan pada sistem. Jika medium menawarkan hambatan dalam pound secara numerik sama dengan tiga kali kecepatan sesaat, yang diukur dalam ft/s, tentukan perpindahan sebagai fungsi waktu.

• Solusi homogen

Diberikan W = 6-lb, asumsikan g = 32 ft/s², diperoleh m = W/g = 6/32 = 3/16 slug.

Diberikan x = 4 in = ⅓ ft, dan F = W = 6-lb, menurut hukum Hooke

F = kx ⇔ 6 = ⅓k ⇔ k = 18 lb/ft.

Diberikan koefisien redaman oleh hambatan medium sebesar a = 3 lb·s/ft

Berdasarkan informasi awal, diperoleh persamaan diferensial

(3/16)x'' + 3x' + 18x = 27·sin(4t) − 3·cos(4t), kalikan masing-masing ruas dengan 16/3

x'' + 16x' + 96x = 144·sin(4t) − 16·cos(4t)

Solusi homogen dapat ditentukan menggunakan persamaan karakteristik

r² + 16r + 96 = 0

(r + 8)² + 32 = 0

r = –8 ±i√32, diperoleh solusi homogen

xₕ = c₁e⁻⁸ᵗ·cos(t√32) + c₂e⁻⁸ᵗ·sin(t√32).

• Solusi partikuler

Diberikan F(t) = 27·sin(4t) − 3·cos(4t), sehingga solusi khususnya berbentuk xₚ = A·cos(4t) + B·sin(4t)

turunkan dua kali

xₚ' = –4A·sin(4t) + 4B·cos(4t)

xₚ'' = –16A·cos(4t) – 16B·sin(4t), masukkan ke persamaan awal

–16A·cos(4t) – 16B·sin(4t) + 16[–4A·sin(4t) + 4B·cos(4t)] + 96[A·cos(4t) + B·sin(4t)] = 144·sin(4t) − 16·cos(4t)

(80A + 64B)·cos(4t) + (–64A + 80B)·sin(4t) = 144·sin(4t) − 16·cos(4t), bagi masing-masing ruas dengan 16

(5A + 4B)·cos(4t) + (–4A + 5B)·sin(4t) = 9·sin(4t) − cos(4t), diperoleh SPL

5A + 4B = −1 ...(i)

–4A + 5B = 9 ...(ii)

4(i) + 5(ii) → 41B = 41 ⇔ B = 1

5(i) – 4(ii) → 41A = –41 ⇔ A = –1

Jadi solusi khususnya adalah xₚ = –cos(4t) + sin(4t)

Solusi totalnya adalah

x = xₕ + xₚ = c₁e⁻⁸ᵗ·cos(t√32) + c₂e⁻⁸ᵗ·sin(t√32) – cos(4t) + sin(4t), turunkan terhadap t

x' = –8c₁e⁻⁸ᵗ·cos(t√32) – (√32)c₁e⁻⁸ᵗ·sin(t√32) – 8c₂e⁻⁸ᵗ·sin(t√32) + (√32)c₂e⁻⁸ᵗ·cos(t√32) + 4·sin(4t) + 4·cos(4t)

Diberikan beban berhenti di posisi kesetimbangan, jadi x(0) = 0; juga beban dilepaskan dari keadaan diam, jadi x'(0) = 0; masukkan ke x dan x'

c₁·cos(0) + c₂·sin(0) – cos(0) + sin(0) = 0 ⇔ c₁ = 1

–8c₁·cos(0) – (√32)c₁·sin(0) – 8c₂·sin(0) + (√32)c₂·cos(0) + 4·sin(0) + 4·cos(0) = 0 ⇔ –8c₁ + (√32)c₂ + 4 = 0, masukkan c₁ = 1

(√32)c₂ – 4 = 0 ⇔ c₂ = √½

Jadi, perpindahannya adalah x = e⁻⁸ᵗ·cos(t√32) + (√½)e⁻⁸ᵗ·sin(t√32) – cos(4t) + sin(4t)

4. Sebuah pegas koil tertentu dengan konstanta pegas 10 lb/ft digantung dari langit-langit. Sebuah beban 32-lb dipasang di ujung bawah pegas dan berhenti di posisi kesetimbangannya. Dimulai pada t = 0, sebuah gaya eksternal yang diberikan oleh F(t) = sin(t) + ¼sin(2t) + ⅛sin(3t) diterapkan pada sistem. Medium menawarkan hambatan dalam pound secara numerik sama dengan dua kali kecepatan sesaat, yang diukur dalam kaki per detik. Tentukan perpindahan beban sebagai fungsi waktu.

(Minfor mempersilahkan kepada Sixtyfourians untuk mencoba sendiri)

5. Sebuah beban seberat 12-lb dipasang pada ujung bawah pegas koil yang digantung dari langit-langit. Beban tersebut berhenti pada posisi keseimbangannya sehingga meregangkan pegas sejauh 6 inci. Dimulai pada t = 0, sebuah gaya eksternal yang diberikan oleh F(t) = 2·cos(ωt) diterapkan pada sistem. Jika gaya redaman dalam pound secara numerik sama dengan 3(dx/dt), di mana dx/dt adalah kecepatan sesaat dalam ft/s, tentukan frekuensi resonansi dari gerakan yang dihasilkan dan temukan perpindahan sebagai fungsi waktu ketika fungsi gaya berada dalam resonansi dengan sistem.

• Solusi homogen

Diberikan W = 12-lb, asumsikan g = 32 ft/s², diperoleh m = W/g = 12/32 = ⅜ slug.

Diberikan x = 6 in = ½ ft, dan F = W = 12-lb, menurut hukum Hooke

F = kx ⇔ 12 = ½k ⇔ k = 24 lb/ft.

Diberikan koefisien redaman oleh hambatan medium sebesar a = 3 lb·s/ft

Frekuensi resonansi (ω) terjadi ketika amplitudo getaran maksimum. Frekuensi resonansi diberikan oleh rumus:

Berdasarkan informasi awal, diperoleh persamaan diferensial

⅜x'' + 3x' + 24x = 2·cos(ωt), kalikan masing-masing ruas dengan 8/3

x'' + 8x' + 64x = (16/3)·cos(ωt)

Solusi homogen dapat ditentukan menggunakan persamaan karakteristik

r² + 8r + 64 = 0

(r + 4)² + 48 = 0

r = –4 ± 4i√3, diperoleh solusi homogen

xₕ = c₁e⁻⁴ᵗ·cos(4t√3) + c₂e⁻⁴ᵗ·sin(4t√3)

• Solusi partikuler

Diberikan F(t) = (16/3)·cos(ωt), solusi partikuler berbentuk xₚ = A·cos(ωt) + B·sin(ωt), turunkan dua kali

xₚ' = –ωA·sin(ωt) + ωB·cos(ωt)

xₚ'' = –ω²A·cos(ωt) – ω²B·sin(ωt)

masukkan ke persamaan awal

–ω²A·cos(ωt) – ω²B·sin(ωt) + 8[–ωA·sin(ωt) + ωB·cos(ωt)] + 64[A·cos(ωt) + B·sin(ωt)] = (16/3)·cos(ωt)

[–ω²A + 8ωB + 64A]·cos(ωt) + [–ω²B – 8ωA + 64B]·sin(ωt) = (16/3)·cos(ωt), diperoleh

–ω²A + 8ωB + 64A = 16/3 ⇔ (–3ω² + 192)A + 24ωB = 16

–ω²B – 8ωA + 64B = 0 ⇔ –8ωA + (–ω² + 64)B = 0

masukkan ω = √32 = 4√2

96A + (96√2)B = 16 ⇔ 6A + (6√2)B = 1 ...(i)

(–32√2)A + 32B = 0 ⇔ (–√2)A + B = 0 ...(ii)

(i) – (6√2)(ii) → 18A = 1 ⇔ A = 1/18

(i) + (3√2)(ii) → (9√2)B = 1 ⇔ B = (√2)/18

Jadi, solusi partikulernya adalah:

xₚ = (1/18)·cos(t√32) + [(√2)/18]·sin(t√32)

Perpindahan sebagai fungsi waktu, dengan asumsi keadaan tunak, adalah solusi partikuler:

xₚ = (1/18)·cos(t√32) + [(√2)/18]·sin(t√32)

6. Sebuah beban seberat 20-lb dipasang pada ujung bawah pegas koil yang digantung dari langit-langit. Beban tersebut berhenti pada posisi keseimbangannya, sehingga meregangkan pegas sejauh 6 inci. Berbagai gaya eksternal dalam bentuk F(t) = cos(ωt) diterapkan pada sistem dan ditemukan bahwa frekuensi resonansi adalah 0,5 siklus/detik. Dengan asumsi bahwa hambatan medium dalam pound secara numerik sama dengan a(dx/dt), di mana dx/dt adalah kecepatan sesaat dalam kaki per detik, tentukan koefisien redaman a.

Diberikan W = 20-lb, asumsikan g = 32 ft/s², diperoleh m = W/g = 20/32 = ⅝ slug.

Diberikan x = 6 in = ½ ft, dan F = W = 20-lb, menurut hukum Hooke

F = kx ⇔ 20 = ½k ⇔ k = 40 lb/ft.

Diberikan frekuensi resonansi f = 0,5 siklus/detik, sehingga frekuensi sudut = ω = 2π·(0,5) = π rad/s

Ingat kembali rumus frekuensi resonansi sudut:

kuadratkan kedua ruas

ω² = k/m – a²/(2m²) = 40/(⅝) – a²/(2⅝²) = 64 – (32/25)a², kalikan masing-masing ruas dengan 25/32

(25/32)ω² = 50 – a²

a² = 50 – (25/32)ω² = 50 – (25/32)π² ≈ 42,28937, akarkan masing-masing ruas

a ≈ 6,503028

Jadi, koefisien redaman a adalah 6,503028

7. Persamaan diferensial untuk gerakan massa satuan pada pegas koil tertentu di bawah pengaruh gaya eksternal berbentuk F(t) = 30·cos(ωt) adalah x'' + ax' + 24x = 30·cos(ωt), dimana a ≥ 0 koefisien redaman.

a. Gambarkan kurva resonansi dari sistem untuk a = 0, 2, 4, 6, dan 4√3.

Diberikan m = 1, k = 24

Diberikan F(t) = 30·cos(ωt), berarti F₁ = 30

Secara umum, berikut ini bentuk untuk f(ω)

sehingga berikut ini grafiknya

b. Jika a = 4, temukan frekuensi resonansi dan tentukan amplitudo getaran keadaan tunak ketika fungsi gaya berada dalam resonansi dengan sistem.

Ingat kembali rumus frekuensi resonansi sudut:

= √(24 – 4²/2) = √16 = 4 rad/s, masukkan ke f(ω)

= ¾√5 ≈ 1,677051

Jadi, frekuensi resonansi adalah 4 rad/s dan amplitudo getaran keadaan tunak saat resonansi adalah 1,677051.