Sudut Pusat dan Sudut Keliling Lingkaran

1. Hubungan Sudut Pusat dengan Sudut Keliling

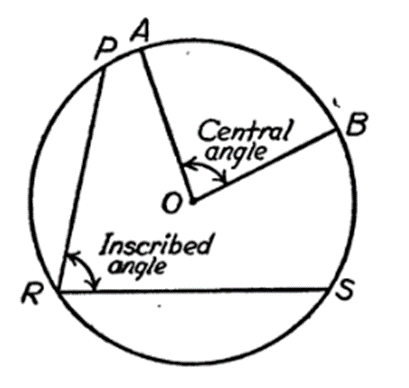
Sudut pusat (Central angle) adalah sudut yang dibentuk oleh dua jari-jari, sedangkan sudut keliling adalah sudut yang dibentuk oleh dua tali busur.

Sudut keliling yang menghadap busur yang sama mempunyai besar setengah sudut pusat. Perhatikan gambar berikut:

Perhatikan ∆𝐴𝑂𝑃

|AO| = |PO| karena jari-jari lingkaran, sehingga ∆𝐴𝑂𝑃 samakaki

∠𝐴𝑃𝑂 = ∠𝑃𝐴𝑂 = 𝑘 (karena |AO| = |PO|)

∠𝐴𝑂𝑃 = 180° − ∠𝐴𝑃𝑂 − ∠𝑃𝐴𝑂 = 180 − 2𝑘 

Perhatikan |PC|:

∠𝐴𝑂𝐶 = 180° − ∠𝐴𝑂𝑃 (karena berpelurus)

∠𝐴𝑂𝐶 = 180° − (180° − 2𝑘) 

∠𝐴𝑂𝐶 = 2𝑘 

Perhatikan ∆𝐵𝑂𝑃

|BO| = |PO| karena jari-jari lingkaran, sehingga ∆𝐵𝑂𝑃 samakaki

∠𝐵𝑃𝑂 = ∠𝑃𝐵𝑂 = 𝑙 (karena |BO| = |PO|)

∠𝐵𝑂𝑃 = 180° − ∠𝐵𝑃𝑂 − ∠𝑃𝐵𝑂 = 180 − 2𝑙 

Perhatikan |PC|:

∠𝐵𝑂𝐶 = 180° − ∠𝐵𝑂𝑃 (karena berpelurus)

∠𝐵𝑂𝐶 = 180° − (180° − 2𝑙) 

∠𝐵𝑂𝐶 = 2𝑙

∠𝐴𝑂𝐵 = ∠𝐴𝑂𝐶 + ∠𝐵𝑂𝐶 

∠𝐴𝑂𝐵 = 2𝑘+2𝑙 

∠𝐴𝑂𝐵 = 2(𝑘+𝑙) 

∠𝐴𝑂𝐵 = 2(∠𝐴𝑃𝑂 + ∠𝐵𝑃𝑂) 

∴ 𝐴𝑂𝐵 = 2∠𝐴𝑃𝐵 

Jika cara yang sama diterapkan pada ∠𝐴𝑄𝐵 maka akan diperoleh ∠𝐴𝑂𝐵 = 2∠𝐴𝑄𝐵

Sehingga ∠𝐴𝑃𝐵 = ∠𝐴𝑄𝐵 = ½∠𝐴𝑂𝐵 (Terbukti)

Dari sini kita mendapati bahwa semua sudut keliling yang menghadap busur yang sama besarnya sama, yaitu setengah sudut pusat.

2. Sudut Keliling Luar

Perhatikan gambar berikut:

Sudut keliling luar memiliki letak yang lebih jauh dibandingkan sudut pusat dan sudut keliling. Dengan menarik tali busur dari A ke C dan B ke D menjadi:

∠AOB dan ∠COD merupakan sudut pusat, ∠ADB, ∠DAC, ∠BCA, ∠CBD merupakan sudut keliling, sedangkan ∠AMB yang berhimpit dengan ∠DMC merupakan sudut keliling luar.

Telah dibahas bahwa sudut pusat adalah sudut antara 2 jari-jari, sudut keliling adalah sudut antara 2 tali busur, sedangkan sudut keliling adalah sudut antara 2 secant.

Misalkan ∠AOB = θ dan ∠COD = φ, diperoleh ∠ADB = ∠ACB = ½θ dan ∠CAD = ∠CBD = ½φ.

Karena ∠ADB dan ∠MDB berpelurus, ∠MDB = 180° - ½θ, selanjutnya perhatikan segitiga MDB

Jumlah sudut segitiga adalah 180°, sehingga berlaku ∠MDB + ∠DBM + ∠BMD = 180°

180° - ½θ + ½φ + ∠BMD = 180°

- ½θ + ½φ + ∠BMD = 0

∠BMD = ½θ - ½φ

∠BMD = ½(θ - φ)

∴ ∠AMB = ½(∠AOB - ∠COD)

Jadi, besar sudut keliling luar adalah setengah selisih sudut pusat yang menghadap kedua busur yang dilalui olehnya.