Kuasa Titik Pada Lingkaran
A. Kuasa Titik Pada Lingkaran
Kuasa titik (x1,
y1) terletak diluar lingkaran maka kuasanya merupakan kuadratnya jarak titik tersebut ke titik singgung lingkaran dari garis singgung yang dibuat dari titik tersebut pada lingkaran.
Diberikan lingkaran berpusat di M, titik B(x1, y1) di luar lingkaran, AB garis singgung lingkaran. Misal lingkaran dengan persamaan x2
+ y2 + Ax + By + C = 0.
Ingat kembali bahwa berlaku persamaan:
|BA|2 = |BE|.|BF| = |BC|.|BD|
Hasil kali ini kuasa titik B terhadap lingkaran L
|BC|.|BD| = (|BM| - r).(|BM| + r) = |BM|2 - r2
= (x1
+ ½A)2 + (y1 + ½B)2 – (¼A2 + ¼B2
– C)
= x12
+ Ax1 + ¼A2 + y12
+ Bx1 + ¼B2 – ¼A2 – ¼B2
+ C
= x12
+ y12 + Ax1 + By1 + C
Jadi, kuasa titik B(x1, y1) pada lingkaran L: x2 + y2 + Ax + By + C = 0 adalah x12 + y12 + Ax1 + By1 + C.
B. Garis Kuasa
Garis Kuasa adalah tempat kedudukan titik-titik yang memiliki kuasa sama terhadap dua lingkaran.
Misal diberikan dua lingkaran dengan persamaan:
L1:
x2 + y2 + A1x + B1y + C1
= 0
L2:
x2 + y2 + A2x + B2y + C2
= 0
Misalkan titik P(x1, y1) memiliki kuasa sama terhadap L1 dan L2 sehingga dipenuhi:
x12 + y12 + A1x1 + B1y1 + C1 = x12 + y12 + A2x1 + B2y1 + C2
(A1 - A2)x1 + (B1 - B2)y1 + C1 - C2 = 0
Jelas bahwa tempat kedudukan tersebut merupakan garis yang melalui titik P, sehingga apabila dijalankan menjadi:
(A1 - A2)x + (B1 - B2)y + C1 - C2 = 0
Gradien garis tersebut adalah -(A1 - A2)/(B1 - B2)
Sedangkan gradien garis perpusatan (garis yang melalui pusat kedua lingkaran) adalah:
Apabila gradien garis kuasa dikalikan dengan gradien garis perpusatan dihasilkan -1, sehingga didapati bahwa garis kuasa tegak lurus dengan garis perpusatan.
C. Titik Kuasa Tiga Lingkaran
Misal diberikan tiga lingkaran dengan persamaan:
L1: x2 + y2 + A1x + B1y + C1 = 0
L2: x2 + y2 + A2x + B2y + C2 = 0
L3: x2 + y2 + A3x + B3y + C3 = 0
Akan dihasilkan 3 garis kuasa yaitu:
L1 - L2 = (A1 - A2)x + (B1 - B2)y + C1 - C2 = 0
L1 - L3 = (A1 - A3)x + (B1 - B3)y + C1 - C3 = 0
L2 - L3 = (A2 - A3)x + (B2 - B3)y + C2 - C3 = 0
Teorema: Ketiga garis kuasa yang dihasilkan berpotongan pada satu titik.
Bukti:
Sebagaimana syarat tiga garis berpotongan pada satu titik, akan ditunjukkan bahwa koefisien dari ketiganya menghasilkan determinan nol:
Perhitungan determinannya sangat panjang, kita ambil satu sampel yang mana polanya akan selalu sama.
Jika cara yang sama diterapkan pada yang lain akan selalu diperoleh nol, sehingga determinannya sama dengan nol, yang artinya ketiganya konkuren. ∎
Untuk menentukan titiknya, cukup potongkan dua garis saja.


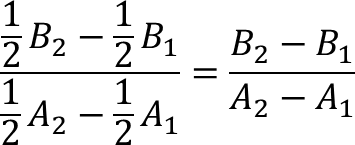





Komentar
Posting Komentar