Perkalian Silang Vektor
1. Perkalian Silang Vektor
Misal u = (u1,
u2, u3) dan v = (v1, v2, v3) merupakan vektor-vektor dalam dimensi tiga. Perkalian silang keduanya, ditulis u × v, adalah vektor yang didefinisikan sebagai:
u × v = (u2v3 − u3v2, u3v1 − u1v3, u1v2 − u2v1)
dapat dinotasikan juga dalam determinan
untuk mempermudah mengingatnya, bisa juga dengan matriks berukuran 2 × 3:
untuk menentukan komponennya, hapus kolom yang bertepatan dengannya, khusus komponen kedua tandanya dilawankan, INGAT kembali kofaktor.
Catatan:
Hasil kali silang vektor merupakan vektor, berbeda dengan hasil kali titik yang merupakan skalar.
2. Sifat-Sifat Perkalian Silang Vektor
Misal u, v, w merupakan vektor dalam R3, berlaku sifat-sifat perkalian silang:
a) Sifat Ortogonal
u ∙ (u × v) = 0
v ∙ (u × v) = 0
Hasil kali silang dua vektor ortogonal terhadap kedua vektor tersebut.
b) Identitas Lagrange
u × (v × w) = (u ∙ w)v − (u ∙ v)w
(u × v) × w = (u ∙ w)v − (v ∙ w)u
3. Sifat-Sifat Aritmatik Perkalian Silang Vektor
Misal u, v, w merupakan vektor dalam R3, dan k sebarang skalar, berlaku sifat-sifat perkalian silang:
a) Sifat Berlawanan Tanda
u × v = −(v × u)
b) Sifat Distributif
u × (v + w) = u × v + u × w
(u + v) × w = u × w + v × w
c) Sifat Skalar
k(u × v) = (ku) × v = u × (kv)
d) Sifat Nol
u × 0 = 0 × u = 0
u × u = 0
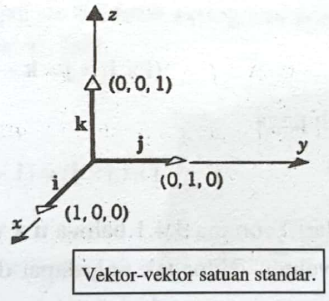
4. Vektor Satuan Standar
Tinjau vektor i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1). Masing-masing memiliki panjang 1 dan terletak pada sumbu koordinat, disebut sebagai vektor satuan standar dalam dimensi tiga. Setiap vektor v = (v1, v2, v3) dalam dimensi tiga dapat dinyatakan dalam i, j, k, sebagaimana berikut:
v = (v1, v2, v3) = v1(1, 0, 0) + v2(0, 1, 0) + v3(0, 0, 1) = v1i + v2j + v3k
Hasil kali silang vektor satuan standar
i × i = j × j = k × k = 0
i × j = k, j × k = i, k × i = j
Hasil kali titik vektor satuan standar
i ∙ i = j ∙ j = k ∙ k = 1
i ∙ j = j ∙ i = j ∙ k = k ∙ j = k ∙ i = i ∙ k = 0
5. Perkalian Silang dalam Determinan
Perkalian silang vektor dapat ditulis dalam bentuk determinan matriks:
Kita tahu bahwa u × v ortogonal terhadap u dan v. Jika u dan v adalah vektor-vektor tak nol, dapat ditunjukkan bahwa arah u × v dapat ditentukan dengan menggunakan "aturan tangan kanan" berikut ini:
Misal θ adalah sudut antara u dan v, dan anggap u diputar dengan sudut θ sampai berimpitan dengan v. Jika jari-jari tangan kanan ditekuk sehingga menunjuk arah putaran, maka ibu jari menunjukkan (kira-kira) arah u × v.
7. Luas Jajargenjang
Ingat kembali identitas Lagrange:
identitas Lagrange ini digunakan untuk menentukan panjang dari hasil kali silang vektor.
Uraikan identitas Lagrange:
dikarenakan 0 ≤ 𝜃 ≤ 𝜋, sin𝜃 tidak mungkin negatif sehingga tidak perlu tanda mutlak.
Perhatikan gambar berikut:
Misalkan sebuah jajargenjang memiliki alas dengan panjang ‖u‖, sisi sampingnya ‖v‖, dan sudut antara alas dengan sisi samping adalah 𝜃. Hasil kali ‖v‖ sin𝜃 sama dengan tinggi jajargenjang, sehingga:
A = (alas)(tinggi) = ‖u‖ ‖v‖ sin𝜃 = ‖u × v‖
Dengan kata lain, berlaku pernyataan:
"Jika u dan v merupakan vektor-vektor dalam dimensi 3, maka panjang ‖u × v‖ sama dengan luas jajargenjang yang dibentuk oleh u dan v"
8. Perkalian Skalar Ganda Tiga
Perkalian skalar ganda tiga dari u, v, dan w didefinisikan sebagai:
u ∙ (v × w)
Lalu bagaimana rumus untuk perkalian skalar ganda tiga u ∙ (v × w)?
Ingat kembali perkalian skalar, perkalian silang vektor, dan vektor satuan standar:
u ∙ (v × w) = w ∙ (u × v) = v ∙ (w × u)
ingat kembali sifat-sifat aritmatik perkalian silang vektor, sehingga diperoleh identitas:
u ∙ (v × w) = w ∙ (u × v) = v ∙ (w × u) = -u ∙ (w × v) = -w ∙ (v × u) = -v ∙ (u × w)
-u ∙ (v × w) = -w ∙ (u × v) = -v ∙ (w × u) = u ∙ (w × v) = w ∙ (v × u) = v ∙ (u × w)



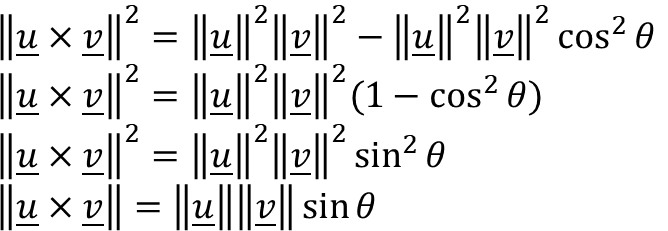




Komentar
Posting Komentar