Kombinasi Linear Vektor dan Rentang

1. Ruang Penyelesaian untuk Sistem-Sistem Homogen

Jika Ax = b adalah suatu sistem persamaan linear, maka setiap vektor x yang memenuhi persamaan ini disebut suatu vektor penyelesaian dari sistem tersebut. Teorema berikut ini menunjukkan bahwa vektor penyelesaian dari suatu sistem linear homogen membentuk suatu ruang vektor, yang akan kita sebut sebagai ruang penyelesaian dari sistem tersebut.

Teorema: "Jika Ax = 0 adalah suatu sistem linear homogen dari m persamaan dalam n variabel, maka himpunan vektor penyelesaiannya adalah suatu subruang dari R-n". Bukti:

Anggap W adalah himpunan vektor penyelesaian. Paling tidak ada satu vektor dalam W, yaitu 0. Untuk menunjukkan bahwa W tertutup terhadap penjumlahan dan perkalian skalar, kita harus menunjukkan bahwa jika x dan x' adalah sembarang vektor-vektor penyelesaian dan k adalah sembarang skalar, maka x + x' dan kx juga merupakan vektor-vektor penyelesaian. Akan tetapi, jika x dan x' adalah vektor-vektor penyelesaian, maka Ax = 0 dan Ax' = 0, jumlahkan kedua persamaan menjadi

A(x + x') = Ax + Ax' = 0 + 0 = 0, juga A(kx) = kAx = k0 = 0 yang membuktikan bahwa x + x' dan kx juga vektor-vektor penyelesaian. ■

2. Kombinasi Linear Vektor

Definisi: "Suatu vektor w disebut suatu kombinasi linear dari vektor-vektor v₁, v₂, ..., v_r jika dapat dinyatakan dalam bentuk w = k₁v₁ + k₂v₂ + ... + k_rv_r; dengan k₁, k₂, ..., k_r skalar".

Setiap vektor v = (a, b, c) di R3 dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor satuan standar yaitu i = (1, 0, 0), j = (0, 1, 0), dan k = (0, 0, 1), karena:

v = (a, b, c) = a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1) = ai + bj + ck.

3. Kesubruangan Kombinasi Linear Vektor

Jika v₁, v₂, ..., v_r adalah vektor-vektor dalam suatu ruang vektor V, maka secara umum beberapa vektor dalam V mungkin merupakan kombinasi linear dari v₁, v₂, ..., v_r dan yang lainnya mungkin tidak. Teorema berikut ini menunjukkan bahwa jika kita menyusun suatu himpunan W yang terdiri dari semua vektor-vektor yang dapat dinyatakan sebagai kombinasi linear dari v₁, v₂, ..., v_r itu, maka W membentuk suatu subruang dari V.

Teorema: Jika v₁, v₂, ..., v_r adalah vektor-vektor dalam suatu ruang vektor V, maka:

a) Himpunan W yang terdiri dari semua kombinasi linear dari v₁, v₂, ..., v_r merupakan suatu subruang dari V.

b) W adalah subruang terkecil dari V yang berisi v₁, v₂, ..., v_r dalam pengertian bahwa setiap subruang lain dari V yang berisi v₁, v₂, ..., v_r pasti mengandung W.

Bukti (a):

Ambil sebarang vektor u dan v yang merupakan anggota W, misalkan:

u = c₁v₁ + c₂v₂ + ... + c_rv_r dan v = k₁v₁ + k₂v₂ + ... + k_rv_r, jumlah keduanya adalah:

u + v = (c₁ + k₁)v₁ + (c₂ + k₂)v₂ + ... + (c_r + k_r)v_r, yang juga merupakan anggota W.

Ambil sebarang skalar k, kalikan dengan u, ku = (kc₁)v₁ + (kc₂)v₂ + ... + (kc_r)v_r, yang juga merupakan anggota W.

Dikarenakan operasi penjumlahan dan perkalian skalar pada W bersifat tertutup, W merupakan subruang dari V. ■

Bukti (b):

Setiap vektor v_i dapat dinyatakan sebagai kombinasi linier v = 0v₁ + 0v₂ + ... + 1v_i + ... + 0v_r. Oleh karena itu subruang W mengandung vektor-vektor v₁, v₂, ..., v_r. Anggap W' adalah sebarang subruang lainnya yang mengandung v₁, v₂, ..., v_r. Karena W' tertutup terhadap penjumlahan dan perkalian skalar, maka W' pasti mengandung semua kombinasi linear dari v₁, v₂, ..., v_r. Jadi, W' mengandung setiap vektor dari W. Dengan kata lain W ⊂ W' ⊂ V. ■

4. Rentang

Definisi: Jika S = {v₁, v₂, ..., v_r} adalah suatu himpunan vektor dalam suatu ruang vektor V, maka subruang W dari V yang mengandung semua kombinasi linear dari vektor-vektor dalam S disebut ruang terentang oleh v₁, v₂, ..., v_r dan kita katakan bahwa vektor-vektor v₁, v₂, ..., v_r adalah rentang W. Untuk menunjukkan bahwa W adalah ruang terentang oleh vektor-vektor dalam himpunan S = {v₁, v₂, ..., v_r} kita tuliskan W = rent(S) atau W = rent{v₁, v₂, ..., v_r}.

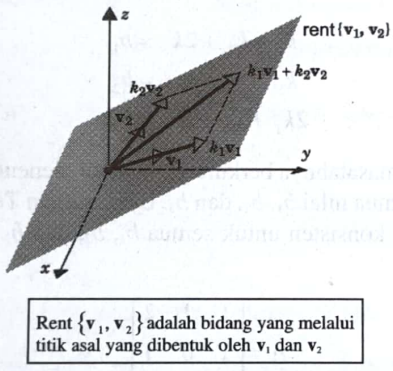
Perhatikan gambar berikut:

Misal diberikan dua vektor v₁ dan v₂ yang tidak kolinear di R3, keduanya berpangkal di O(0, 0, 0). Rent{v₁, v₂} yang berisi semua kombinasi linear k₁v₁ + k₂v₂, adalah bidang yang memuat keduanya.

Misal diberikan vektor taknol v di R2 atau R3 yang berpangkal di O. Rent{v} yang merupakan himpunan semua perkalian skalar kv, adalah garis yang memuat v.

Polinomial 1, x, x², ..., xⁿ merentangkan ruang vektor P_n karena setiap polinomial p dalam P_n dapat ditulis sebagai:

p = a₀ + a₁x + a₂x² + ... + a_nxⁿ

yang merupakan suatu kombinasi linear dari 1, x, x², ..., xⁿ. Kita dapat menyatakan rentang ini sebagai:

P_n = rent(1, x, x², ..., xⁿ)

Misal S = {v₁, v₂, ..., v_r} dan S' = {w₁, w₂, ..., w_r} keduanya himpunan vektor dalam suatu ruang vektor V, berlaku teorema berikut:

rent{v₁, v₂, ..., v_r} = rent{w₁, w₂, ..., w_r} jika dan hanya jika setiap vektor dalam S adalah suatu kombinasi linear dari vektor-vektor dalam S', dan sebaliknya setiap vektor dalam S' adalah suatu kombinasi linear dari vektor-vektor dalam S.