Momen (Stadas)

Definisi: Momen dapat diartikan sebagai harga harapan dari data 𝑋 yang dipangkatkan r.
Misalkan diberikan variabel 𝑥 dengan nilai-nilai x1, x2, …, xn. Jika 𝐴 adalah suatu konstanta dan 𝑟 = 0, 1, 2, …, 𝑛, maka Momen ke-r disekitar A, yaitu mr', didefinisikan sebagai berikut:
Catatan: Rerata dan Variansi merupakan hal khusus dari kelompok ukuran lain yang disebut Momen. Nilai 𝐴 dan 𝑟 dapat disesuaikan sehingga pada kasus-kasus khusus akan menjadi nilai dari ukuran pemusatan (Rata-rata) atau penyebaran (Variansi).

1. Momen Non-Sentral
Jika nilai A = 0 maka momen ke-r disekitar A = 0 (disebut momen ke-𝑟 terhadap titik asal O atau momen nonsentral ke-r) didefinisikan sebagai berikut:
Beberapa momen non-sentral pertama:
➢ Momen non-sentral ke-1 di sekitar titik O:
Momen ke-1 ini disebut sebagai rerata.
➢ Momen non-sentral ke-2 di sekitar titik O:
➢ Momen non-sentral ke-3 di sekitar titik O:
dan seterusnya...

2. Momen Sentral
Jika nilai A = x ̅ maka momen ke-r disekitar A = x ̅  (disebut momen ke-𝑟 disekitar rata-rata atau momen sentral ke-r) didefinisikan sebagai berikut :
Beberapa momen sentral pertama:
➢ Momen sentral ke-1 di sekitar rerata:
Momen sentral ke-1 ini bernilai nol, ingat kembali definisi rerata.
➢ Momen sentral ke-2 di sekitar rerata:
Momen sentral ke-2 inilah yang disebut sebagai variansi.
➢ Momen sentral ke-3 di sekitar rerata:
dan seterusnya...

3. Hubungan Momen Sentral dengan Momen Non-Sentral
Jika mr' adalah momen non-sentral ke-r dan mr adalah momen sentral ke-r, maka berikut ini hubungan antara momen sentral dengan momen non-sentral:
➢ Untuk r = 1:
Ingat kembali rerata, jelas bahwa m1 = 0.
➢ Untuk r = 2:
m2 = m2' – (m1')2     
➢ Untuk r = 3:
m3 = m3' – 3.m2'.m1' + 2(m1')3     
➢ Untuk r = 4:
m4 = m4' – 4.m3'.m1' + 6.m2'.(m1')2 – 3(m1')4    
Secara umum, hubungan momen sentral dengan momen non-sentral adalah:

4. Momen Data Berkelompok
Jika data telah disusun kedalam tabel dsitribusi frekuensi, dengan  dan xi menyatakan tanda kelas interval, dan fi menyatakan frekuensi yang sesuai dengan xi, maka momennya adalah
• Momen ke-r di sekitar A
• Momen non-sentral
• Momen sentral
contoh soal:
Tentukan momen non-sentral dan momen sentral kedua dari data berikut:
Hitung rerata yang akan digunakan untuk menentukan momen sentral
rerata = 3950/100 = 39,5
Berikut tabel perhitungannya
Momen non-sentral kedua dari data tersebut adalah 170525/100 = 1705,25
Momen sentral kedua dari data tersebut adalah 14500/100 = 145

5. Jenis Rerata dan Momen
A. Rerata Aritmatika
Rerata aritmatika sama dengan momen ke-1 non-sentral.
B. Rerata Geometri
Tidak ada momen yang sama dengan rerata geometri karena momen merupakan penjumlahan sedangkan rerata geometri merupakan rerata perkalian.
C. Rerata Harmonik
Rerata harmonik sama dengan resiprokal dari momen ke-(–1).
D. Rerata Kuadrat
Rerata kuadrat sama dengan akar dari momen ke-2 non-sentral.

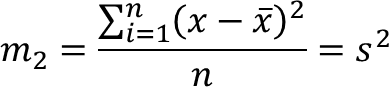
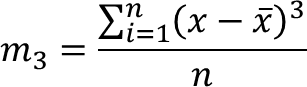
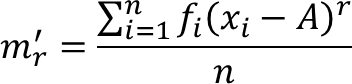
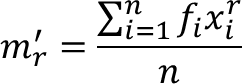
Komentar

Posting Komentar

Postingan populer dari blog ini

Rotasi Baru (Komposisi Geseran dan Rotasi)

Gambar
1. Komposisi Geseran dengan Rotasi Untuk sebarang titik A, B, P, dan besar sudut θ, selalu dapat ditemukan titik C sehingga: a. S AB R P, θ  = R C, θ   Misal terdapat dua garis sejajar r dan s dengan jarak antara keduanya adalah ½|AB|, sehingga dipenuhi S AB  = M r M s . Misal terdapat garis t yang memotong s di P dengan sudut antara s dan t adalah ½θ, sehingga dipenuhi R P, θ  = M s M t . Kita dapat menguraikan S AB R P, θ  = (M r M s )(M s M t ) = M r M s M s M t   = M r IM t   = M r M t , karena r sejajar s, sudut antara r dan t juga ½θ, misal r dan t berpotongan di C = R C, θ   b. R P, θ S AB  = R C, θ   Misal terdapat dua garis sejajar r dan s dengan jarak antara keduanya adalah ½|AB|, sehingga dipenuhi S AB  = M s M r . Misal terdapat garis t yang memotong s di P dengan sudut antara s dan t adalah ½θ, sehingga dipenuhi R P, θ  = M t M s . Kita dapat menguraikan R P, θ S AB  = M t M s M s M r   = M t ...
Read more »

2024: Aritmatika Jilid XII

Gambar
Aritmatika adalah event tahunan yang diselenggarakan oleh Himpunan Mahasiswa Pendidikan Matematika Universitas Sebelas Maret Surakarta. Dalam Aritmatika jilid XII terdapat tiga rangkaian acara yaitu Lomba Olimpiade Matematika, Lomba Media Pembelajaran Matematika Tingkat Nasional, dan Lomba Microteching tingkat Nasional. 1. Olimpiade Matematika Lomba ini diperuntukkan bagi siswa SMP, SMA, atau sederajat dari seluruh Indonesia. Lomba ini bersifat individu, tidak berkelompok. Setiap sekolah dibolehkan mengirimkan lebih dari satu delegasi. Timeline untuk olimpiade ini sebagai berikut: 1 s/d 20 Juli 2024: Pendaftaran Gelombang 1, dengan biaya pendaftaran Rp 40.000 untuk SMP dan Rp 45.000 untuk SMA. 22 Juli s/d 10 Agustus 2024: Pendaftaran Gelombang 2, dengan biaya pendaftaran Rp 45.000 untuk SMP dan Rp 50.000 untuk SMA. 12 s/d 25 Agustus 2024: Pendaftaran Gelombang 3, dengan biaya pendaftaran Rp 50.000 untuk SMP dan Rp 55.000 untuk SMA. 1 September 2024: Technical Meeting (Online) 7 Septemb...
Read more »

Kombinasi Linear Vektor dan Rentang

Gambar
1. Ruang Penyelesaian untuk Sistem-Sistem Homogen Jika A x = b adalah suatu sistem persamaan linear, maka setiap vektor x yang memenuhi persamaan ini disebut suatu vektor penyelesaian dari sistem tersebut. Teorema berikut ini menunjukkan bahwa vektor penyelesaian dari suatu sistem linear homogen membentuk suatu ruang vektor, yang akan kita sebut sebagai ruang penyelesaian dari sistem tersebut. Teorema: "Jika A x = 0 adalah suatu sistem linear homogen dari m persamaan dalam n variabel, maka himpunan vektor penyelesaiannya adalah suatu subruang dari R-n". Bukti: Anggap W adalah himpunan vektor penyelesaian. Paling tidak ada satu vektor dalam W, yaitu 0 . Untuk menunjukkan bahwa W tertutup terhadap penjumlahan dan perkalian skalar, kita harus menunjukkan bahwa jika x dan x ' adalah sembarang vektor-vektor penyelesaian dan k adalah sembarang skalar, maka x + x ' dan k x juga merupakan vektor-vektor penyelesaian. Akan tetapi, jika x dan x ' adalah vektor-vekt...
Read more »