Ruang Baris, Ruang Kolom, Ruang Nol
1. Vektor Baris dan Vektor Kolom
Diberikan matriks A berukuran m × n
dan vektor-vektor
2. Ruang Baris, Ruang Kolom, Ruang Nol
Definisi: "Jika A adalah suatu matriks m × n, maka subruang dari R-n yang terentang oleh vektor-vektor baris dari A disebut ruang baris dari A, dan subruang dan R-m yang terentang oleh vektor-vektor kolom disebut ruang kolom dari A, ruang solusi dari sistem persamaan homogen Ax = 0, yang merupakan suatu subruang dari R-n, disebut ruang nol dari A."
Diberikan matriks A dan vektor x sebagai berikut:
Kita mendapati bahwa hasil kali Ax dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor kolom ini dengan koefisien dari x; yaitu:
Ax = x1c1
+ x2c2 + … + xncn
Jadi, suatu sistem linear, Ax = b, dari m persamaan dalam n variabel dapat ditulis sebagai:
x1c1 + x2c2 + … + xncn = b
dari persamaan ini kita simpulkan bahwa Ax = b konsisten jika dan hanya jika b dapat dinyatakan sebagai suatu kombinasi linear dari vektor-vektor kolom dari A atau, secara ekuivalen, jika dan hanya jika b berada dalam ruang kolom A. Hal ini dapat dinyatakan sebagai:
"Suatu sistem persamaan linear Ax = b konsisten jika dan hanya jika b berada dalam ruang kolom A"
3. Hubungan antara solusi Ax = 0 dan Ax = b
Teorema: Jika x0 menyatakan sembarang solusi tunggal dari suatu sistem linear tak homogen yang konsisten Ax = b, dan jika v1, v2, ..., vk membentuk suatu basis untuk ruang nol A, yaitu ruang solusi dari sistem homogen Ax = 0, maka setiap solusi dari Ax = b dapat dinyatakan dalam bentuk
x = x0 + c1v1 + c2v2 + … + ckvk,
dan sebaliknya, untuk semua pilihan skalar c1, c2, ..., cn vektor x dalam rumus ini merupakan suatu solusi dari Ax = b.
Bukti:
(i) Diberikan x0 adalah sembarang solusi tetap dari Ax = b, dan x sembarang solusi, sehingga:
Ax0 = b dan Ax = b
Kurangkan keduanya menjadi:
Ax0 – Ax = 0, faktorkan menjadi:
A(x – x0) = 0
yang menunjukkan bahwa x – x0 adalah solusi dari sistem homogen Ax = 0.
Karena v1, v2, ..., vk adalah suatu basis untuk ruang solusi dari sistem ini, kita dapat menyatakan x – x0 sebagai suatu kombinasi linear dari vektor-vektor ini
x – x0 = c1v1 + c2v2 + … + ckvk
x = x0 + c1v1 + c2v2 + … + ckvk
(ii) Untuk semua pilihan skalar c1, c2, ..., cn kita dapatkan:
x = x0 + c1v1 + c2v2 + … + ckvk, kalikan masing-masing ruas dengan A:
Ax = A(x0 + c1v1 + c2v2 + … + ckvk), sebarkan
Ax = Ax0 + c1(Av1) + c2(Av2) + ... + ck(Avk)
Dikarenakan x0 solusi dari sistem tak homogen dan v1, v2, ..., vk adalah solusi dari sistem homogen, persamaan terakhir menjadi:
Ax = b + 0 + 0 + ... + 0 = b
yang menunjukkan bahwa x adalah penyelesaian dari Ax = b. ■
4. Solusi Umum dan Solusi Khusus
Misal vektor x0 merupakan solusi khusus dari Ax = b. Bentuk x0 + c1v1 + c2v2 + … + ckvk merupakan solusi umum dari Ax = b, sedangkan bentuk c1v1 + c2v2 + … + ckvk merupakan solusi umum dari Ax = 0. Dengan ini, solusi umum dari Ax = b adalah penjumlahan dari sembarang solusi khusus dari Ax = b dan solusi umum dari Ax = 0.
Untuk sistem linear dengan dua atau tiga variabel, interpretasi geometrinya cukup bagus dalam R² dan R³. Misalkan suatu kasus di mana Ax = 0 dan Ax = b adalah sistem linear dengan dua variabel. Solusi dari Ax = 0 membentuk sebuah subruang dari R² dan karenanya merupakan garis yang melalui titik O, hanya titik O, atau seluruh R². Solusi dari Ax = b dapat diperoleh dengan menambahkan sembarang solusi khusus dari Ax = b, misalkan x0, ke solusi dari Ax = 0. Dengan asumsi bahwa x0 diposisikan dengan titik awalnya di titik asal, hal ini memiliki efek geometrik menggeser ruang solusi dari Ax = 0, sehingga titik asal dipindahkan ke ujung x0. Ini berarti bahwa vektor-vektor solusi dari Ax = b membentuk garis melalui ujung x0, titik di ujung x0, atau seluruh R².
Demikian pula, untuk sistem linear dengan tiga variabel, solusi dari Ax = b membentuk bidang melalui ujung sembarang solusi khusus x0, garis melalui ujung x0, titik di ujung x0, atau seluruh R³.
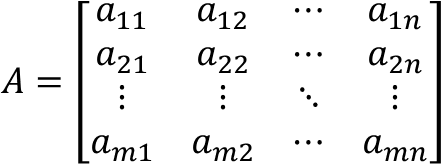









Komentar
Posting Komentar