Distribusi Normal
Distribusi normal (distribusi Gauss) merupakan distribusi kontinu yang paling banyak digunakan dalam analisis statistik. Grafik distribusi normal disebut kurva Normal berbentuk seperti lonceng. Kurva normal berbentuk seperti lonceng, simetris terhadap nilai rata-rata (𝜇). Kurva normal sangat baik untuk menggambarkan sekelompok data yang muncul dalam kehidupan. Sebagian besar nilai berada di sekitar rerata, dan semakin jauh dari rerata semakin kecil frekuensinya.
1. Sifat-Sifat Kurva Normal
A. Asimtotik terhadap sumbu mendatar (Sumbu X)
B. Simteris terhadap garis 𝑥 = 𝜇
C. Memiliki titik maksimum di
D. Memiliki dua titik belok yang berjarak 𝜎 dari sumbu simetri
E. Luas daerah diatas sumbu X dan dibawah kurva setara dengan satu satuan luas. Karena kurva Normal simetris,berbentuk lonceng dan unimodal maka daerah di di kanan dan di kiri garis tegak lurus diatas mean masing-masing besarnya 0,5
F. Merupakan kurva unimodal, karena mean = median = mode
2. Fungsi Normal
Variabel random X berdistribusi normal (distribusi Gauss) dengan parameter 𝛼 dan 𝛽 jika fungsi densitasnya sebagai berikut:
Distribusi normal sering dinyatakan dengan 𝑁(𝛼, 𝛽²) atau 𝑋~𝑁(𝛼, 𝛽²).
Lebih khusus lagi parameter 𝛼 diganti dengan 𝜇 dan 𝛽 diganti dengan 𝜎, bentuk fungsinya menjadi:
3. Distribusi Normal Baku
Jika distribusi normal memiliki parameter 𝛼 = 0 dan 𝛽 = 1, maka variabel random X berdistribusi normal baku (standar), yaitu 𝑁(0, 1) yang sering disebut distribusi Z, dengan fungsi densitas:
4. Integral Utuh
Luas daerah di bawah kurva normal (baik normal biasa maupun normal baku) dan di atas sumbu mendatar (absis) adalah 1 satuan.
Jika variabel random kontinu X berdistribusi normal, yaitu 𝑋~𝑁(𝜇, 𝜎²), maka variabel random
berdistribusi normal baku. Hal ini menunjukkan bahwa transformasi dari distribusi normal 𝑁(𝛼, 𝛽²) menjadi distribusi normal baku N(0, 1) dapat dilakukan dengan mentransformasi menggunakan rumus transformasi Z ini.
5. Peluang dari Interval
Pada distribusi normal biasa, peluang bahwa X terletak diantara a dan b yang ditulis 𝑃(𝑎 < 𝑋 < 𝑏) dihitung dengan rumus:
yang merupakan luas daerah di bawah kurva normal biasa, di atas sumbu X dan dibatasi oleh garis x = a dan garis x = b.
Hanya saja pengunaan rumus di atas tidak semudah yang diharapakan, sehingga untuk mempermudah perhitungan dapat digunakan tabel Z yang menyatakan luas daerah di bawah kurba normal baku, di atas sumbu Z, dan dibatasi oleh Z = 0, dan Z = z, dengan terlebih dahulu mentransformasi variabel X ke variabel Z. Akibatnya peluang X diantara a dan b dicari dengan :
dan berikut versi half nya:
versi full berisi positif dan negatif, sedangkan versi half hanya berisi positif.
versi full berisi positif dan negatif, sedangkan versi half hanya berisi positif.
Peluang yang tertulis di tabel full adalah peluang bahwa bilangan baku kurang dari Z.
Adapun untuk tabel half, peluang sebenarnya adalah:
0,5 + peluang tertulis, untuk positif
0,5 − peluang tertulis, untuk negatif
contoh soal:
Suatu ujian dengan 20000 peserta, nilai reratanya 51,24 dan deviasi baku 16.
1. Jika data terdistribusi normal, berapakah peserta dengan nilai 45 kebawah?
Untuk nilai 45, bilangan bakunya adalah:
Pada tabel full, peluangnya adalah 0,3483. Sehingga banyak peserta dengan nilai 45 kebawah adalah 0,3483 × 20000 = 6966. Jadi, ada 6966 peserta dengan nilai 45 kebawah.
2. Jika nilai minimal untuk lulus adalah 65, maka berapa persen yang lulus?
Untuk nilai 65, bilangan bakunya adalah:
Pada tabel full, peluangnya adalah 0,8051. Peluang mendapatkan nilai 65 keatas adalah 1 − 0,8051 = 0,1949. Jadi, peserta yang lulus adalah 19,49%.
3. Jika terdapat 7,93% peserta yang memperoleh nilai dengan predikat memuaskan, maka berapa nilai minimal (terendah) untuk memperoleh nilai predikat memuaskan?
Jika terdapat 7,93% dengan predikat memuaskan, peluang tidak mendapatkan predikat memuaskan adalah 100% − 7,93% = 92,07% = 0,9207.
Pada tabel full, peluang 0,9207 dengan bilangan baku 1,41. Nilai minimal untuk memperoleh predikat memuaskan adalah:
𝑋 = 𝜇 + 𝑍𝜎 = 51,24 + 1,41 × 16 = 73,8
Jadi, nilai minimal untuk memperoleh predikat memuaskan adalah 73,8.
4. Berapa banyak peserta dengan nilai diantara 41 dan 57?
Untuk nilai 41 bilangan bakunya adalah:
Untuk nilai 57 bilangan bakunya adalah:
P(41 < X < 57) = P(X < 57) − P(X < 41) = 0,6406 − 0,2611 = 0,3795
n(41 < X < 57) = 0,3795 × 20000 = 7590
Jadi, terdapat 7590 peserta dengan nilai diantara 41 dan 57.
6. Hubungan Distribusi Normal dengan Binomial
Distribusi binomial dapat didekati oleh distribusi normal jika memenuhi dua syarat :
A. n cukup besar (n > 30)
B. Peluang kejadian yaitu 𝑃(𝑋) tidak terlalu dekat ke nol atau satu.
Hubungan dari distribusi normal dengan distribusi binomial adalah:
Jika X adalah distribusi binomial dengan rata-rata 𝜇 = 𝑛𝑝 dan variansi 𝜎² = 𝑛𝑝(1 − 𝑝) untuk 𝑝 adalah peluang kejadian sukses, maka dengan mengambil limit dari
maka Z terdistribusi normal baku.
Rumus transformasi untuk mendapatkan distribusi normal baku dari distribusi binomial adalah:
Rumus transformasi untuk mendapatkan distribusi normal baku dari distribusi binomial adalah:
Karena ada perubahan dari variabel diskrit ke kontinu, maka nilai 𝑋 mengalami penyesuaian, yaitu 𝑋 ± 0,5
contoh:
Dalam suatu ujian terdapat 40 soal dengan soal ujian berbentuk pilihan ganda dengan 5 alternatif pilihan, seseorang menjawab dengan hanya menebak saja. Peluang orang tersebut menjawab benar antara 5 sampai 10 soal ditentukan dengan menggunakan distribusi normal baku yang merupakan hasil transformasi dari distribusi binomial adalah...
Kejadian pada masalah di atas adalah kejadian pada binomial, karena hanya terdapat dua kemungkinan, yaitu sukses atau tidak sukses dari hasil menebak. Akan tetapi, banyak soal relatif lebih banyak, yaitu 𝑛 = 40 sehingga 𝑃(5 ≤ 𝑋 ≤ 10) ditentukan dengan distribusi normal baku.
Peluang menjawab benar, yaitu 𝑝 = 1/5 (terdapat 1 jawaban benar dari 5 alternatif pilihan), sehingga
𝜇 = 𝑛𝑝 = 40 × 1/5 = 8
𝜎² = 𝑛𝑝(1 − 𝑝) = 10 × (1 − 1/5) = 6,4
Bilangan baku untuk X = 5 adalah:
Bilangan baku untuk X = 10 adalah:
Silahkan lihat kembali tabel Z yang full, akan didapati:
P(5 ≤ 𝑋 ≤ 10) ≈ 0,667562393Jadi, peluang menjawab benar antara 5 sampai 10 soal adalah 0,667562393.


















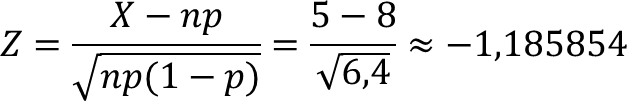



Komentar
Posting Komentar