Uji Normalitas dan Uji Homogenitas

1. Uji Normalitas
Uji normalitas digunakan untuk menguji apakah suatu sampel berasal dari populasi berdistribusi normal atau tidak. Dalam praktiknya, uji normalitas bukan hanya sebatas asumsi, akan tetapi sesuatu yang dipersyaratkan sehingga harus dilakukan pengujian untuk normalitas, sehingga pada beberapa uji statistika harus dipenuhi dahulu normalitasnya.
Beberapa uji statistik yang mensyaratkan uji normalitas adalah statistika parametrik.
• Uji Rata-rata menggunakan uji z dan uji t.
• Analisis Regresi dan Korelasi.
• Analisis Variansi.
• Analisis Kovariansi.
A. Distribusi Normal
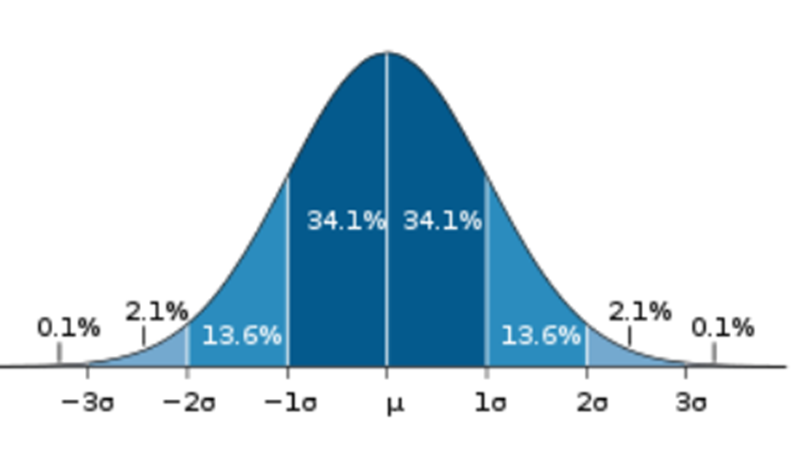
Distribusi Normal (Distribusi Gauss) digambarkan dalam kurva berbentuk lonceng yang simetris terhada nilai rerata 饾渿, yang disebut kurva Normal. Kurva normal sangat baik digunakan untuk menggambarkan sekelompok data yang muncul dalam kehidupan.
Sifat-sifat kurva normal:
1. Asimtotik terhadap sumbu mendatar (Sumbu X)
2. Simteris terhadap garis 饾懃 = 饾渿
3. Memiliki titik maksimum di (饾渿, 1/(饾湈√2饾湅))
4. Memiliki dua titik belok yang berjarak 饾湈 dari sumbu simetri
5. Luas daerah diatas sumbu X dan dibawah kurva setara dengan satu satuan luas. Karena kurva Normal simetris, berbentuk lonceng dan unimodal maka daerah di di kanan dan di kiri garis tegak lurus diatas mean masing-masing besarnya 0,5
6. Merupakan kurva unimodal, karena mean = median = mode
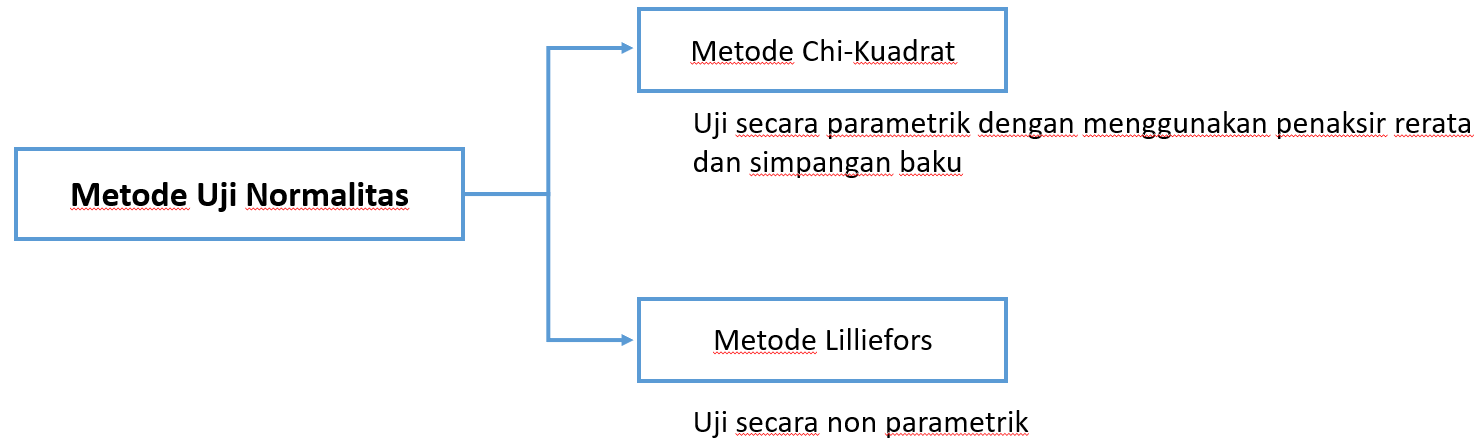
B. Metode Uji Normalitas
Terdapat beberapa metode untuk melakukan uji Normalitas, diantaranya metode Chi-Kuadrat, metode Lilliefors, metode Kolmogorov-Smirnov, metode Shapiro-Wilk, metode Anderson-Darling, metode Jarque-Bera,  metode Ryan-Joiner (similar to Shapiro-Wilk) dan sebagainya, termasuk juga dengan menggunakan grafik (Normal Q-Q Plot).
C. Metode Chi Kuadrat
Uji normalitas dengan metode Chi-Kuadrat dirumuskan sebagai:
Dengan nilai 饾湌² mendekati nilai variabel chi-kuadrat.
饾憸饾憱: frekuensi amatan (observed)
饾憭饾憱: frekuensi harapan (expected)
➢ Penggunaan metode Chi-Kuadrat untuk uji normalitas dilakukan pada data dalam bentuk tabel distribusi frekuensi (data bergolong). Prinsip utamanya dengan membandingkan antara histogram data amatan dengan histogram yang kurva poligon frekuensinya mendekati distribusi normal.  
➢ Derajat kebebasan (dk) untuk uji normalitas dengan metode Chi-Kuadrat adalah k − 1.
Hipotesis statistik 
饾惢0: Sampel berasal dari populasi berdistribusi normal
饾惢1: Sampel tidak berasal dari populasi berdistribusi normal
Statistik Uji
Daerah Kritis
Nilai kritis chi kuadrat dari Tabel Chi-Kuadrat dengan derajat kebebasan (dk) yaitu 饾憳 − 1 untuk 饾憳 adalah banyak kelas dalam Tabel Distribusi Frekuensi.
contoh:
Diberikan data nilai rerata dari 6 mata pelajaran (Matematika, Biologi, Fisika, Kimia, Ekonomi - Sejarah, Sosiologi - Geografi) dari 91 siswa kelas X sebagai berikut:

80,42

78,33

76,33

81,50

77,92

74,75

79,33

77,50

81,67

79,33

89,00

82,67

83,08

82,00

77,50

85,58

77,50

83,17

83,00

76,58

77,42

75,75

74,17

80,00

81,58

81,83

80,58

75,50

75,17

74,25

75,00

78,25

80,58

78,33

82,83

75,00

74,42

77,00

81,00

81,33

79,08

79,08

80,67

75,92

84,00

80,42

73,42

74,83

79,08

77,08

78,08

83,75

77,42

78,58

81,25

74,33

76,08

80,58

81,92

77,17

76,58

79,00

78,08

77,25

75,83

75,67

78,67

78,42

73,50

71,58

81,33

82,92

75,17

75,92

77,42

74,67

76,00

84,67

74,42

78,33

77,33

77,33

72,58

72,25

82,58

76,08

78,00

76,33

74,83

75,08

78,25

Dengan menggunakan 饾浖 = 5%, apakah data tersebut berdistribusi normal?
Perhatikan beberapa langkah berikut yang harus dilakukan dalam melakukan komputasi.
1. Hipotesis Statistika 
饾惢0: Data berdistribusi normal
饾惢1: Data tidak berdistribusi normal
2. Taraf Signifikansi 
伪 = 0,05
3. Statistik Uji
reratanya adalah 78,3
standar deviasinya adalah 3,288
bilangan baku terkecil adalah −2,045 dan yang terbesar adalah 3,252. Pada umumnya banyak kelas adalah pembulatan keatas dari selisih bilangan baku terbesar dan terkecil.
饾憳 = ⌈zmax − zmin⌉ = ⌈3,252 − (−2,045)⌉ = 6
panjang kelasnya adalah 2,9028. Susun tabel distribusi frekuensi:

Interval

Frekuensi

71,58 – 74,48

10

74,49 – 77,38

28

77,39 – 80,29

25

80,30 – 83,19

23

83,19 – 86,09

4

86,10 – 89,00

1

Susun tabel frekuensi harapan dengan bilangan baku (z):

Interval baku

e

–2,04517 s/d –1,16231

9,2943

–1,16231 s/d –0,27945

24,333

–0,27945 s/d 0,60341

30,6609

0,60341 s/d 1,48628

18,6107

1,48628 s/d 2,36914

5,4316

2,36914 s/d 3,25200

0,7591

Cara untuk menentukan frekuensi harapan adalah tentukan peluang dikalikan banyak data.
e = P(a < z < b) * n
untuk peluang bisa dilihat di tabel z.
Tentukan nilai Chi Kuadrat

Interval

o

e

o – e

(o – e)²

(o – e)²/e

71,58 – 74,48

10

9,294348

0,705652

0,497944

0,053575

74,49 – 77,38

28

24,33301

3,666988

13,4468

0,552616

77,39 – 80,29

25

30,6609

–5,6609

32,04583

1,045169

80,30 – 83,19

23

18,61074

4,389256

19,26557

1,035185

83,19 – 86,09

4

5,431629

–1,43163

2,049563

0,377338

86,10 – 89,00

1

0,759104

0,240896

0,058031

0,076447

Total

3,14033

Nilai Chi kuadratnya adalah 3,14033
4. Daerah Kritis
5. Keputusan Uji dan Kesimpulan
Karena nilai 饾湌² = 3,14033; maka 饾湌² < 11,070498. Hal ini berarti 饾湌² ∉ 饾惙饾惥 akibatnya 饾惢0 diterima. Dengan kata lain, data terdistribusi normal.
D. Metode Lilliefors
Pengujian normalitas menggunakan metode Lilliefors jika data tidak dalam bentuk tabel distribusi frekuensi/data bergolong. 
Metode perhitungan untuk metode Lilliefors.
➢ Data diurutkan berdasarkan nilai (dari nilai terkecil ke terbesar atau sebaliknya), kemudian setiap data pada metode Lilliefors di ubah menjadi bilangan baku z dengan tranformasi 
➢ Statistik Uji metode Lilliefors
L = Max|F(zi) − S(zi)|
dengan F(zi) = P(Z ≤ zi); Z ~ 饾憗(0,1)
S(zi) = Proporsi cacah Z ≤ zi terhadap seluruh z
➢ Daerah Kritis
DK = {L | L > L伪;n}
dengan n ukuran sampel dan L伪;n dari tabel Lilliefors:
contoh:
Sebuah sampel berukuran 6 diambil secara random dari suatu populasi. Keenam nilai dari sampel tersebut adalah 
4, 0, 8, 6, 14, 10
Dengan mengambil 饾浖 = 5%, ujilah apakah sampel tersebut berasal dari populasi berdistribusi normal atau tidak?
1. Hipotesis Statistik
饾惢0 : Sampel berasal dari populasi berdistribusi normal
饾惢1 : Sampel tidak berasal dari populasi berdistribusi normal
2. Taraf signifikansi 
伪 = 0,05
3. Statistik Uji
Apabila data yang diberikan dihitung diperoleh reratanya 7 dan standar deviasinya 4,86. Data diurutkan terlebih dahulu (dari kecil ke besar), kemudian setiap data ditransformasi dengan transformasi baku.
Untuk menentukan nilai F(zi), lihat tabel normal baku.
Untuk menentukan nilai S(zi), nomor urut data dibagi banyak data.
Dari tabel terlihat bahwa nilai L hitung = 0,1009 (diambil yang terbesar)
4. Daerah Kritis dan Keputusan Uji
Titik kritis L伪;n = L0,05;6 = 0,319; sehingga 
DK ={L│L > L伪;n}={L│L > L0,05;6}={L│L > 0,319}
Karena L = 0,1009 maka L < 0,319. Hal ini menunjukkan bahwa 饾惪 ∉ 饾惙饾惥, sehingga 饾惢0 diterima.
5. Kesimpulan 
Sampel berasal dari populasi berdistribusi normal. Jadi, berdasarkan uji Lilliefors, sampel data di atas berasal dari populasi yang berdistribusi normal.

2. Uji Homogenitas
Uji homogenitas merupakan uji statistika untuk melihat apakah variansi-variansi dari sejumlah populasi sama (homogen) atau tidak. Uji homogenitas merupakan uji prasyarat untuk beberapa uji statistik lainnya, seperti uji rata-rata dan analisis variansi. Terdapat beberapa statistic uji untuk menguji homogenitas varians antar populasi.
• Untuk menguji varians 饾憳 populasi dapat digunakan uji Bartlett.
• Secara khusus, untuk menguji varians 2 populasi dapat digunakan uji 饾惞.
Hipotesis Statistik
饾惢0: 饾湈i² = 饾湈j²; ∀i, j (Variansi populasi Homogen)
饾惢1: 饾湈i² ≠ 饾湈j²; ∃i, j dengan i ≠ j (Varians populasi Tidak Homogen)
dengan i = 1, 2, ..., 饾憳 dan j = 1, 2, ..., 饾憳.
A. Uji Homogenitas 饾憳 populasi
➢ Uji homogenitas untuk 饾憳 populasi dapat dilakukan dengan menggunakan uji Bartlett. Adapun statistik uji yang digunakan adalah:
dengan:
• 饾憼1², 饾憼1²,…, 饾憼饾憳² adalah varians dari setiap sampel berukuran 饾憶1, 饾憶2, …, 饾憶饾憳 dengan rumusan:
• 饾憼饾憹² adalah varians gabungan yang dirumuskan:
untuk 饾憗 = 饾憶1 + 饾憶2 + … + 饾憶饾憳 
➢ Daerah Kritis
DK = {b│b < b饾憳(伪; 饾憶1, 饾憶2, …, 饾憶饾憳)} dengan
b饾憳(伪; 饾憶饾憱) dapat dilihat pada tabel Bartlett untuk 饾憶饾憱 menunjukkan banyak anggota kelompok ke-i.
Tabel Bartlett untuk 伪 = 0,01 dan 伪 = 0,05:
contoh:
Untuk menguji apakah model A, B, dan C memiliki varians yang sama, secara random diambil sampel acak sebanyak 4 buah untuk model A, 6 buah untuk model B, dan 5 buah untuk model C dengan data sebagai berikut.
A : 4, 7, 6, 6
B : 5, 1, 3, 5, 3, 4
C : 8, 6, 8, 9, 5
Dengan menggunakan 饾浖 = 5%, bagaimanakah kesimpulan penelitian?
Diketahui : N = 15, 饾憳 = 3 (banyak kelompok), 饾憶1 = 4, 饾憶2 = 6, dan 饾憶3 = 5.
1. Hipotesis Statistik
饾惢0: 饾湈1² = 饾湈2² = 饾湈3² (Variansi ketiga populasi sama)
饾惢1: Tidak semua varians sama (Varians ketiga populasi tidak sama)
2. Taraf Signifikansi
伪 = 0,05
3. Statistik Uji
a. Menghitung varians sampel dan varians gabungan
b. Menghitung nilai b
4. Daerah Kritis dan Keputusan Uji
Titik kritis 饾憦3(0,05; 4) = 0,4669; 饾憦3(0,05; 6) = 0,6483; 饾憦3(0,05; 5) = 0,5762 (tabel Bartlett)
DK = {b | b < 饾憦3(0,05; 4, 6, 5) }={b | b < 0,5767}
Karena 饾憦 = 0,9805 maka 饾憦 > 0,5767. Hal ini berarti 饾憦 ∉ 饾惙饾惥, akibatnya 饾惢0 diterima.
5. Kesimpulan
Varians-varians dari ketiga populasi sama (homogen).
B. Bentuk Lain Uji Bartlett
Statistik uji homogenitas (Uji Bartlett) dengan Chi-Kuadrat
Keterangan
饾憳: Banyak populasi = Banyak sampel
N: Banyak seluruh nilai
饾憶饾憲: Banyak nilai sampel ke-j = ukuran sampel ke-j 
饾憮饾憲 = 饾憶饾憲 − 1: Derajat kebebasan untuk 饾憼饾憲²; j = 1, 2, 3, …, k
饾憮 = 饾憗 − 饾憳 = ∑饾憮饾憲: Derajat kebebasan untuk RKG
Daerah Kritis
contoh:
Untuk menguji apakah model A, B, dan C memiliki varians yang sama, secara random diambil sampel acak sebanyak 4 buah untuk model A, 6 buah untuk model B, dan 5 buah untuk model C dengan data sebagai berikut.
A : 4, 7, 6, 6
B : 5, 1, 3, 5, 3, 4
C : 8, 6, 8, 9, 5
Dengan menggunakan 饾浖 = 5%, bagaimanakah kesimpulan penelitian?
1. Hipotesis Statistik
饾惢0: 饾湈1² = 饾湈2² = 饾湈3² (Variansi ketiga populasi sama)
饾惢1: Tidak semua varians sama (Varians ketiga populasi tidak sama)
2. Taraf Signifikansi
伪 = 0,05
3. Statistik Uji
饾憮1 = 4 − 1 = 3; 
饾憮2 = 6 − 1 = 5; 
饾憮3 = 5 − 1 = 4; 
f = ∑饾憮饾憲 = 3 + 5 + 4 = 12
Tabel bantu untuk SS sebagai berikut:
SS1 = 137 − 132,25 = 4,75
Untuk SS2 dan SS3 apabila dilakukan cara yang sama akan diperoleh SS2 = 11,5 dan SS3 = 10,8
Tabel bantu untuk 饾湌² sebagai berikut:
饾憮 × log⁡(饾憛饾惥饾惡) = 12 × log(2,254) = 12(0,353) = 4,326
4. Daerah Kritis
5. Keputusan Uji
Karena 饾湌² = 0,216 maka 饾湌² < 5,991465. Hal ini berarti 饾湌² ∉ 饾惙饾惥, sehingga 饾惢0 diterima.
6. Kesimpulan
Varians-varians dari ketiga  populasi tersebut adalah sama (homogen).
C. Kasus Khusus: Uji Homogenitas Dua Populasi Independen
Hipotesis Statistik 
饾惢0: 饾湈1² = 饾湈2² 
饾惢1: 饾湈1² ≠ 饾湈2² 
dengan 饾湈1² varians populasi ke-1; 饾湈2² variansi populasi ke-2. 
Statistik Uji F
Daerah Kritis
dengan
饾懀1 = 饾憶1 − 1 untuk 饾憶1 adalah ukuran sampel dengan varians terbesar
饾懀2 = 饾憶2 − 1 untuk 饾憶2 adalah ukuran sampel dengan varians terkecil
Contoh
Misalkan disajikan skor ujian statistika dari dua kelas sebagai berikut:
Kelas A : 5, 5, 6, 7, 8, 8, 9, 9
Kelas B : 5, 5, 6, 6, 6, 7, 7, 8
Dengan menggunakan taraf signifikansi 5%, apakah kedua populasi dari kedua kelas tersebut homogen?
1. Hipotesis
饾惢0: 饾湈1² = 饾湈2² (Varians kedua populasi homogen)
饾惢1: 饾湈1² ≠ 饾湈2² (Varians kedua populasi tidak homogen)
dengan 饾湈1² varians populasi kelas A; 饾湈2² variansi populasi kelas B.
2. Taraf Signifikansi
饾浖 = 0,05
3. Statistik Uji
sehingga sA² = 2,696 > sB² = 1,071
4. Daerah Kritis dan Keputusan Uji
Karena F = 2,517 maka F < 3,79. Hal ini menunjukkan bahwa 饾惞 ∉ 饾惙饾惥, sehingga 饾惢0 diterima.
5. Kesimpulan
Varians dari kedua populasi homogen.  

3. Hubungan Uji Normalitas, Homogenitas, dan Komparasi Rerata
Berikut disajikan hubungan dan alur pengujian antara uji normalitas, uji homogenitas, dan uji rerata:
Uji normalitas untuk menentukan apakah data akan diuji parametrik atau non-parametrik. Suatu data diuji parametrik jika dan hanya jika terdistribusi normal.
Untuk uji parametrik, uji homogenitas untuk menentukan apakah data akan diuji reratanya menggunakan t atau t'. Untuk data yang homogen dilakukan uji t, sedangkan data yang tidak homogen dilakukan uji t'.

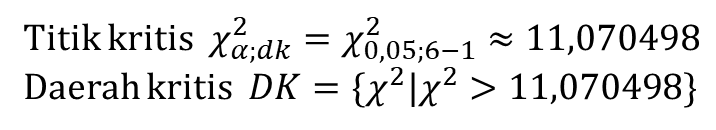
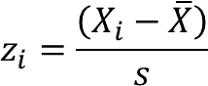
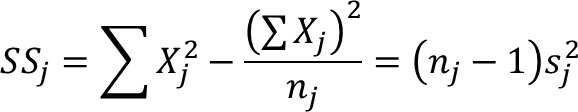
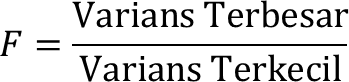
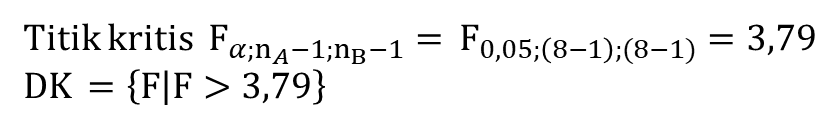
Komentar

Posting Komentar

Postingan populer dari blog ini

Uji Linearitas dan Keberartian Regresi

Gambar
1. Uji Linearitas Regresi ➢ Analisis regresi mengharuskan adanya hubungan fungsional antara X dan Y yang linear → perubahan nilai di salah satu variabel independen akan menghasilkan perubahan yang konstan pada variabel dependen. ➢ Tujuan linearitas pada regresi adalah meyakinkan hubungan linear pada X dan Y dan juga dampak dari model tersebut. Selain itu, residu tersisa sudah tidak memiliki pola tertentu sehingga memastikan bahwa model yang dikeluarkan benar tepat.  ➢ Tidak dipenuhinya asumsi linearitas menjadikan estimasi parameter regresi menjadi bias (koefisien regresi, kesalahan baku, dan pengujian signifikansi) yang berakibat model regresi menjadi tidak tepat jika digunakan untuk prediksi. ➢ Hasil analisis regresi yang underfitting atau overfitting serta resiko kesalahan tipe I atau tipe II menjadi sangat besar. Berikut langkah-langkah uji linearitas: 1. Urutkan dan Kelompokkan Data Data diurutkan berdasarkan nilai X dari terkecil hingga terbesar. Data dengan nilai X yang sama...
Read more »

Limit dan Kekontinuan Fungsi Dua Variabel

Gambar
Mungkin tampak aneh bahwa kita membahas turunan parsial sebelum limit untuk fungsi dua variabel atau lebih. Namun, diferensiasi parsial sebenarnya merupakan ide yang lebih sederhana karena semua variabel kecuali satu variabel dijaga tetap. Satu-satunya konsep yang diperlukan untuk mendefinisikan turunan parsial adalah limit dari suatu fungsi satu variabel. Di sisi lain, limit dari suatu fungsi dua (atau lebih) variabel adalah konsep yang lebih dalam karena kita harus memperhitungkan semua cara di mana (x, y) mendekati (a, b). Ini tidak dapat disederhanakan menjadi memperlakukan "satu variabel pada satu waktu" seperti diferensiasi parsial. Limit dari suatu fungsi dua variabel memiliki arti intuitif yang biasa: Nilai-nilai f(x, y) semakin mendekati angka L ketika (x, y) mendekati (a, b). Masalahnya adalah bahwa (x, y) dapat mendekati (a, b) dengan cara yang tak terhingga banyaknya. Kita menginginkan definisi yang memberikan L yang sama tidak peduli jalur apa yang diambil (x, y)...
Read more »

Sistem Persamaan Diferensial Linier Homogen Berkoefisien Konstan

Gambar
1. Pengenalan Di halaman ini kita akan membahas sistem linear homogen dx/dt = a₁x + b₁y dy/dt = a₂x + b₂y dimana koefisien a₁, b₁, a₂, dan b₂ adalah konstanta real. Kita mencari solusi dari sistem ini; tapi bagaimana kita harus melanjutkannya? Ingatlah kembali bahwa kita mencari dan menemukan solusi eksponensial dari sistem linear tunggal berderajat n dengan koefisien konstan. Mengingat analogi yang ada antara sistem linear dan persamaan diferensial tingkat-tinggi tunggal, kita sekarang mungkin bisa mencoba menemukan solusi eksponensial dari sistem tersebut. Oleh karena itu mari kita coba tentukan solusi dalam bentuk x = Ae 位t   y = Be 位t   dimana A, B, dan 位 adalah konstanta. Jika kita substitusikan bentuk eksponensial ke dalam persamaan awal, kita mendapatkan A位e 位t  = a₁Ae 位t  + b₁Be 位t   B位e 位t  = a₂Ae 位t  + b₂Be 位t   Persamaan-persamaan ini mengarah langsung ke sistem (a₁ – 位)A + b₁B = 0 a₂A + (b₂ – 位)B = 0 dalam variabel-variabel yang tidak ...
Read more »