Variabel Random Kontinu (Stadas)

Variabel random kontinu merupakan variabel random yang tidak diskrit. Variabel random X disebut variabel random kontinu jika setiap nilai dari X adalah suatu interval pada garis bilangan real (nilainya tidak dapat didaftar).
Nilai variabel random kontinu : −∞ < X < ∞

1. Fungsi Densitas (Fungsi Peluang Variabel Kontinu)
Misalkan X adalah suatu variabel random kontinu. Fungsi 饾憮(饾懃) = P(X = 饾懃) disebut fungsi densitas variabel random X jika dan hanya jika:

2. Peluang Interval
Misalkan X variabel random kontinu yang memiliki fungsi densitas 饾憮(饾懃). Peluang bahwa X terletak antara 饾憥 dan 饾憦, yaitu P(饾憥 < 饾憢 < 饾憦) dinyatakan dengan:
Jika X variabel random kontinu dan 饾憥 < 饾憦 dengan 饾憥 dan b bilangan real, maka:
饾憙(饾憥 ≤ 饾憢 ≤ 饾憦) = 饾憙(饾憥 ≤ 饾憢 < 饾憦) = 饾憙(饾憥 < 饾憢 ≤ 饾憦) = 饾憙(饾憥 < 饾憢 < 饾憦)
Hal ini berlaku dikarenakan variabel X bersifat kontinu, sehingga peluang interval terbuka dan interval tertutup adalah sama, asalkan batas-batasnya sama.
contoh:
Misalkan fungsi densitas peubah acak X adalah:
Tentukan nilai k dan peluang P(1 < X < 3)!
telah diperoleh nilai k, yaitu ½, untuk P(1 < X < 3):
Jadi, peluang nilai X diantara 1 dan 3 adalah ¾.

3. Ekspektasi Variabel Random Kontinu
Misalkan X adalah variabel random kontinu dengan fungsi densitas 饾憮. Ekspektasi (nilai harapan) variabel random kontinu X yang dinotasikan E(X) dirumuskan:
Jika ekspektasi variabel random di atas diperluas, maka diperoleh rumusan:
contoh:
Misalkan fungsi densitas variabel X dinyatakan dengan:
Tentukan nilai 饾惛(饾憢)!
Jadi, nilai ekspektasinya adalah 1.

4. Fungsi Distribusi Kumulatif Kontinu
F(x) adalah fungsi distribusi kumulatif atau fungsi distribusi dari variabel random kontinu X jika dan hanya jika:
Jika X adalah variabel random kontinu dengan fungsi
distribusi F(饾懃) dan fungsi densitas 饾憮(饾懃), maka 
1. P(饾憥 ≤ 饾憢 ≤ 饾憦) = 饾惞(饾憦) − 饾惞(饾憥)
2. Fungsi densitasnya dapat dicari dengan:
Fungsi densitas adalah turunan dari fungsi distribusi.
contoh:
1. Misalkan fungsi densitas variabel X adalah:
Tentukan fungsi distribusi dari X!
Untuk 饾懃 < 0, maka 饾惞(饾懃) = 0
Untuk 0 ≤ 饾懃 < 2:
Untuk 饾懃 ≥ 2:
Jadi fungsi distribusi variabel random kontinu X adalah:
Sehingga P(1 < 饾憢 < 2) = 饾惞(2) − 饾惞(1) = 1 − ¼ = ¾.
2. Diketahui fungsi distribusi variabel kontinu X adalah:
Tentukan fungsi densitas X!
Untuk 饾懃 < 0:
Untuk 0 ≤ 饾懃 < 3:
Untuk 饾懃 ≥ 3:
Sehingga fungsi densitasnya adalah:

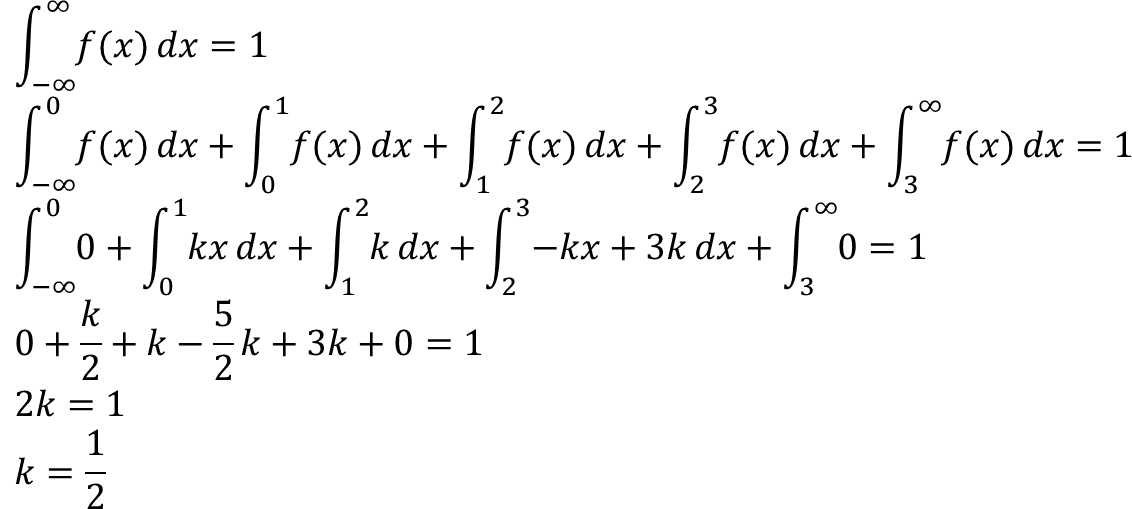
Komentar

Posting Komentar

Postingan populer dari blog ini

Uji Linearitas dan Keberartian Regresi

Gambar
1. Uji Linearitas Regresi ➢ Analisis regresi mengharuskan adanya hubungan fungsional antara X dan Y yang linear → perubahan nilai di salah satu variabel independen akan menghasilkan perubahan yang konstan pada variabel dependen. ➢ Tujuan linearitas pada regresi adalah meyakinkan hubungan linear pada X dan Y dan juga dampak dari model tersebut. Selain itu, residu tersisa sudah tidak memiliki pola tertentu sehingga memastikan bahwa model yang dikeluarkan benar tepat.  ➢ Tidak dipenuhinya asumsi linearitas menjadikan estimasi parameter regresi menjadi bias (koefisien regresi, kesalahan baku, dan pengujian signifikansi) yang berakibat model regresi menjadi tidak tepat jika digunakan untuk prediksi. ➢ Hasil analisis regresi yang underfitting atau overfitting serta resiko kesalahan tipe I atau tipe II menjadi sangat besar. Berikut langkah-langkah uji linearitas: 1. Urutkan dan Kelompokkan Data Data diurutkan berdasarkan nilai X dari terkecil hingga terbesar. Data dengan nilai X yang sama...
Read more »

Limit dan Kekontinuan Fungsi Dua Variabel

Gambar
Mungkin tampak aneh bahwa kita membahas turunan parsial sebelum limit untuk fungsi dua variabel atau lebih. Namun, diferensiasi parsial sebenarnya merupakan ide yang lebih sederhana karena semua variabel kecuali satu variabel dijaga tetap. Satu-satunya konsep yang diperlukan untuk mendefinisikan turunan parsial adalah limit dari suatu fungsi satu variabel. Di sisi lain, limit dari suatu fungsi dua (atau lebih) variabel adalah konsep yang lebih dalam karena kita harus memperhitungkan semua cara di mana (x, y) mendekati (a, b). Ini tidak dapat disederhanakan menjadi memperlakukan "satu variabel pada satu waktu" seperti diferensiasi parsial. Limit dari suatu fungsi dua variabel memiliki arti intuitif yang biasa: Nilai-nilai f(x, y) semakin mendekati angka L ketika (x, y) mendekati (a, b). Masalahnya adalah bahwa (x, y) dapat mendekati (a, b) dengan cara yang tak terhingga banyaknya. Kita menginginkan definisi yang memberikan L yang sama tidak peduli jalur apa yang diambil (x, y)...
Read more »

Sistem Persamaan Diferensial Linier Homogen Berkoefisien Konstan

Gambar
1. Pengenalan Di halaman ini kita akan membahas sistem linear homogen dx/dt = a₁x + b₁y dy/dt = a₂x + b₂y dimana koefisien a₁, b₁, a₂, dan b₂ adalah konstanta real. Kita mencari solusi dari sistem ini; tapi bagaimana kita harus melanjutkannya? Ingatlah kembali bahwa kita mencari dan menemukan solusi eksponensial dari sistem linear tunggal berderajat n dengan koefisien konstan. Mengingat analogi yang ada antara sistem linear dan persamaan diferensial tingkat-tinggi tunggal, kita sekarang mungkin bisa mencoba menemukan solusi eksponensial dari sistem tersebut. Oleh karena itu mari kita coba tentukan solusi dalam bentuk x = Ae 位t   y = Be 位t   dimana A, B, dan 位 adalah konstanta. Jika kita substitusikan bentuk eksponensial ke dalam persamaan awal, kita mendapatkan A位e 位t  = a₁Ae 位t  + b₁Be 位t   B位e 位t  = a₂Ae 位t  + b₂Be 位t   Persamaan-persamaan ini mengarah langsung ke sistem (a₁ – 位)A + b₁B = 0 a₂A + (b₂ – 位)B = 0 dalam variabel-variabel yang tidak ...
Read more »