Kasus-Kasus Istimewa dari Luasan

1. Kasus-Kasus Istimewa dari Kerucut dan Silinder

A. Kerucut Eliptik (Berpenampang Elips) dan Kerucut Sirkular (Berpenampang Lingkaran)

Umumnya dalam persamaan:

Ingat! ciri-ciri kerucut eliptik adalah:

(i) Ketiga variabel berderajat dua

(ii) Dua variabel bertanda sama dan satu variabel bertanda beda

(iii) Tidak ada konstanta

Irisan dari kerucut eliptik dengan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	Titik
XOZ	Garis lurus berpotongan
YOZ	Garis lurus berpotongan
z = k	Ellips, untuk k ≠ 0
y = j	Hiperbola, untuk j ≠ 0
x = i	Hiperbola, untuk i ≠ 0

Terdapat kasus khusus dimana kerucut eliptik (berpenampang elips) menjadi kerucut sirkular (berpenampang lingkaran), yaitu dalam bentuk:

Ketika a = b, kerucut eliptik menjadi kerucut sirkular.
B. Silinder Eliptik dan Silinder Sirkular

Silinder eliptik umumnya dalam bentuk:

Terdapat kasus khusus dimana a = b, sehingga silinder eliptik menjadi silinder sirkular.
C. Silinder Hiperbolik (Berpenampang Hiperbola)

Silinder hiperbolik umumnya berbentuk:

D. Silinder Parabolik (Berpenampang Parabola)

Silinder parabolik umumnya berbentuk:

x² + 2ay = 0

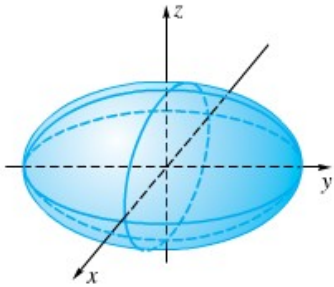
2. Ellipsoid

Umumnya dalam persamaan:

Ingat! ciri-ciri ellipsoid adalah ketika ruas kanan positif, seluruh suku di ruas kiri bertanda positif. Irisan dari ellipsoid dan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	Ellips
XOZ	Ellips
YOZ	Ellips
z = k	Ellips, untuk |k| < c Titik, untuk |k| = c ∅, untuk |k| > c
y = j	Ellips, untuk |j| < b Titik, untuk |j| = b ∅, untuk |j| > b
x = i	Ellips, untuk |i| < a Titik, untuk |i| = a ∅, untuk |i| > a

Terdapat kasus istimewa dari ellipsoid, yaitu sferoid dimana a = b ∨ a = c ∨ b = c.

Terdapat kasus yang lebih istimewa lagi, yaitu sfera atau bola dimana a = b = c.

3. Hiperboloid Satu Lembar

Umumnya dalam persamaan:

Ingat! ciri-ciri hiperboloid satu lembar adalah ketika ruas kanan positif, dua suku di ruas kiri bertanda positif dan satu suku bertanda negatif. Irisan dari hiperboloid satu lembar dan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	Ellips
XOZ	Hiperbola
YOZ	Hiperbola
z = k	Ellips
y = j	Hiperbola
x = i	Hiperbola

4. Hiperboloid Dua Lembar

Umumnya dalam persamaan:

Ingat! ciri-ciri hiperboloid dua lembar adalah ketika ruas kanan positif, satu suku di ruas kiri bertanda positif dan dua suku bertanda negatif. Irisan dari hiperboloid dua lembar dan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	∅
XOZ	Hiperbola
YOZ	Hiperbola
z = k	Ellips, untuk |k| > c Titik, untuk |k| = c ∅, untuk |k| < c
y = j	Hiperbola
x = i	Hiperbola

5. Paraboloid Eliptik

Umumnya dalam persamaan:

Ingat! ciri-ciri paraboloid eliptik adalah:

(i) Dua variabel berderajat dua dan keduanya bertanda sama
(ii) Satu variabel berderajat satu

(iii) Tidak ada konstanta

Irisan dari paraboloid eliptik dengan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	Titik
XOZ	Parabola
YOZ	Parabola
z = k	Ellips, untuk k > 0 ∅, untuk |k| < 0
y = j	Parabola
x = i	Parabola

6. Paraboloid Hiperbolik

Umumnya dalam persamaan:

Ingat! ciri-ciri paraboloid hiperbolik adalah:

(i) Dua variabel berderajat dua dan keduanya bertanda beda
(ii) Satu variabel berderajat satu

(iii) Tidak ada konstanta

Irisan paraboloid hiperbolik dengan bidang datar tertentu:

Bidang Pengiris	Irisan yang Terbentuk
XOY	Garis lurus berpotongan
XOZ	Parabola
YOZ	Parabola
z = k	Hiperbola
y = j	Parabola
x = i	Parabola