Koordinat Titik-Titik Kolinear

1. Sebuah Titik Kolinear dengan Kedua Titik Lainnya

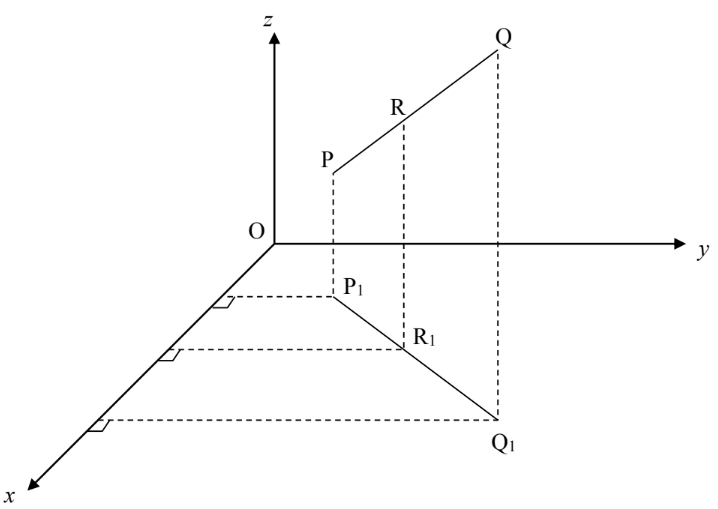
Misal titik P(x₁, y₁, z₁) dan Q(x₂, y₂, z₂) dihubungkan oleh segmen garis, dan titik R(x, y, z) terletak pada segmen PQ dengan perbandingan PR : PQ = λ₁ : λ₂ = λ : 1. Dengan menggunakan kesebangunan segitiga (secara analog) dapat ditentukan koordinat R sebagai berikut:

• Untuk R terletak antara P dan Q nilai λ positif. Lebih khusus lagi untuk R terletak tepat pada pertengahan PQ nilai λ = 1.

• Untuk R diluar PQ sepihak dengan P, nilai lambda pada interval –1 < λ < 0

• Untuk R diluar PQ sepihak dengan Q, nilai lambda pada interval λ < –1

• Untuk R berhimpit dengan P nilai λ tidak terdefinisikan, untuk R berhimpit dengan Q nilai λ = 0, untuk P berhimpit dengan Q nilai λ = –1.

2. Perbandingan Harmonis

Misalkan titik P terletak pada segmen garis AB dan Q diluar segmen AB

rombongan 4 titik tersebut merupakan rombongan 4 titik yang harmonis jika PA/PB = QA/QB

P disebut titik harmonis ke-4 dari Q terhadap A dan B

A disebut titik harmonis ke-4 dari B terhadap P dan Q

Jika dua titik P dan Q terletak terhadap titik-titik A dan B pada garis lurus melalui A dan B demikian, sehingga nilai λ untuk P dan Q adalah sama tetapi berlawanan, dapat ditulis λ(P) = –λ(Q), maka kita katakan, bahwa pasangan titik A dan B dipisahkan harmonis oleh pasangan titik P dan Q.

Jika A(x₁, y₁, z₁), B(x₂, y₂, z₂), dan  maka