Persamaan Luasan

Tempat kedudukan titik dimana koordinat x, y, z terdapat hubungan yang dinyatakan oleh suatu persamaan f(x, y, z) = 0 merupakan suatu persamaan luasan/permukaan bidang lengkung atau bidang datar.

1. Persamaan yang Bebas dari Satu Variabel, Tabung / Silinder

A. Tabung atau Silinder

Misal suatu kurva C dan l adalah garis yang memotong C tapi tidak sebidang dengan C. Semua garis yang sejajar dengan l dan memotong C akan membentuk permukaan yang di sebut tabung. Kurva C dinamakan kurva pembangun.

Garis-garis pelukis suatu tabung bisa saja tidak sejajar dengan sumbu manapun. Untuk kasus khusus dimana garis pelukis sejajar dengan salahsatu sumbu, persamaannya terbebas dari variabel yang bertepatan dengannya.

B. Persamaan yang Bebas dari Satu Variabel

• Persamaan f(x, y) = 0 menyatakan sebuah silinder dengan semua garis pelukisnya sejajar sumbu Z.

• Persamaan f(x, z) = 0 menyatakan sebuah silinder dengan semua garis pelukisnya sejajar sumbu Y.

• Persamaan f(y, z) = 0 menyatakan sebuah silinder dengan semua garis pelukisnya sejajar sumbu X.

contoh:

Misal diberikan persamaan x² + y² = 9, terbentuk silinder berikut:

2. Persamaan yang Hanya Mengandung Satu Variabel

• Persamaan f(x) = 0 : Himpunan bidang datar yang sejajar YOZ

• Persamaan f(y) = 0 : Himpunan bidang datar yang sejajar XOZ

• Persamaan f(z) = 0 : Himpunan bidang datar yang sejajar XOY

contoh:

Persamaan x² = 9 dipenuhi oleh bidang x = 3 dan bidang x = −3.

3. Persamaan Bidang

A. Bentuk Umum

Bentuk umum persamaan bidang adalah Ax + By + Cz + D = 0, dengan A ≠ 0 ∨ B ≠ 0 ∨ C ≠ 0.

contoh: Bidang dengan persamaan 2x + 3y + 6z − 6 = 0.

Untuk menentukan titik potong bidang dengan masing-masing sumbu adalah masukkan nilai 0 ke variabel lain.

B. Persamaan Bidang Melalui Tiga Titik

Misal diberikan tiga titik P₁(x₁, y₁, z₁), P₂(x₂, y₂, z₂), dan P₃(x₃, y₃, z₃). Dikarenakan titik terletak pada bidang Ax + By + Cz + D = 0 tentunya memenuhi:

x₁A + y₁B + z₁C + D = 0 (i)

x₂A + y₂B + z₂C + D = 0 (ii)

x₃A + y₃B + z₃C + D = 0 (iii)

Sebagaimana kita ketahui bahwa A, B, C merupakan koefisien, sedangkan d merupakan konstanta, kita dapat memindahkan konstanta ke ruas kanan sehingga terbentuklah SPL sebagai berikut:

x₁A + y₁B + z₁C = −D (i)

x₂A + y₂B + z₂C = −D (ii)

x₃A + y₃B + z₃C = −D (iii)

Untuk menentukan persamaan bidang melalui tiga titik bisa dengan menyelesaikan SPL tersebut. SPL yang dibentuk oleh tiga titik yang terletak pada bidang selalu memiliki solusi karena apabila terdapat baris nol, secara otomatis nilai D sama dengan nol.

Selain menggunakan SPL, persamaan bidang melalui tiga titik juga bisa diselesaikan menggunakan vektor.

• Pilih salahsatu titik sebagai titik pangkal, misal P₁(x₁, y₁, z₁)

• Buat dua vektor yang berpangkal di P₁(x₁, y₁, z₁) dan ujungnya masing-masing di P₂(x₂, y₂, z₂) dan P₃(x₃, y₃, z₃)

• Kalikan silang kedua vektor, diperoleh vektor normal (vektor yang tegak lurus dengan bidang)

Misal P(x, y, z) sebarang titik pada bidang, berlaku:

Pada akhirnya, persamaan bidang melalui tiga titik dapat ditentukan menggunakan determinan matriks 3 × 3 berikut:

Kembali ke vektor normal, kita memperoleh rumus untuk menentukan koefisien A, B, C, D:

C. Tiga Titik Kolinear

Misal diberikan tiga titik P₁(x₁, y₁, z₁), P₂(x₂, y₂, z₂), dan P₃(x₃, y₃, z₃) yang mana ketiganya kolinear (terletak pada satu garis lurus), SPL yang terbentuk:

x₁A + y₁B + z₁C = −D (i)

x₂A + y₂B + z₂C = −D (ii)

x₃A + y₃B + z₃C = −D (iii)

memiliki tak hingga solusi. Hal ini terjadi ketika determinan dari matriks koefisiennya nol, dengan kata lain:

4. Permukaan Kuadrik

Permukaan dalam ruang dimensi tiga yang persamaannya berderajat dua dinamakan permukaan kuadrik. Bentuk umum persamaan kuadrik adalah:

Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0.

Dengan melakukan rotasi, koefisien D, E, F dapat dihilangkan.

Dengan melakukan translasi, koefisien G, H, I dapat dihilangkan (jika memungkinkan).

Sehingga dapat diperoleh bentuk tereduksi paling sederhana Ax² + By² + Cz² + J = 0 atau Ax² + By² + Iz = 0. Bentuk sederhana ini berpusat di O(0, 0, 0) dan sumbu-sumbu utamanya sama tidak miring.

Berikut ini beberapa contoh permukaan kuadrik istimewa:

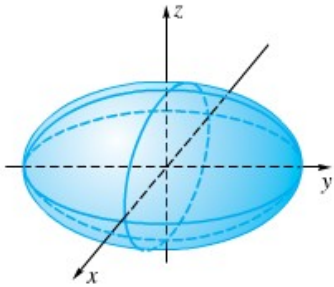
A. Ellipsoid

Umumnya dalam persamaan:

Ingat! ciri-ciri ellipsoid adalah ketika ruas kanan positif, seluruh suku di ruas kiri bertanda positif.

B. Hiperboloid Satu Lembar

Umumnya dalam persamaan:

Ingat! ciri-ciri hiperboloid satu lembar adalah ketika ruas kanan positif, dua suku di ruas kiri bertanda positif dan satu suku bertanda negatif.
C. Hiperboloid Dua Lembar

Umumnya dalam persamaan:

Ingat! ciri-ciri hiperboloid dua lembar adalah ketika ruas kanan positif, satu suku di ruas kiri bertanda positif dan dua suku bertanda negatif.
D. Paraboloid Eliptik

Umumnya dalam persamaan:

Ingat! ciri-ciri paraboloid eliptik adalah:

(i) Dua variabel berderajat dua dan keduanya bertanda sama
(ii) Satu variabel berderajat satu

(iii) Tidak ada konstanta

E. Paraboloid Hiperbolik

Umumnya dalam persamaan:

Ingat! ciri-ciri paraboloid eliptik adalah:

(i) Dua variabel berderajat dua dan keduanya bertanda beda
(ii) Satu variabel berderajat satu

(iii) Tidak ada konstanta

F. Kerucut Eliptik

Umumnya dalam persamaan:

Ingat! ciri-ciri kerucut eliptik adalah:

(i) Ketiga variabel berderajat dua

(ii) Dua variabel bertanda sama dan satu variabel bertanda beda

(iii) Tidak ada konstanta