Basis Ortonormal dan Proses Gram-Schmidt
1. Himpunan Ortonormal
Sebuah himpunan vektor dalam suatu ruang hasil kali dalam disebut himpunan ortogonal jika semua pasangan vektor yang berbeda dalam himpunan tersebut saling ortogonal. Sebuah himpunan ortogonal di mana setiap vektor memiliki norm 1 disebut himpunan orthonormal.
Contoh:
Himpunan S = {u1, u2, u3} dengan u1 = (0, 1, 0), u2 = (1, 0, 1), u3 = (1, 0, −1). Himpunan S merupakan himpunan ortogonal karena 〈u1, u2〉 = 〈u1, u3〉 = 〈u2, u3〉 = 0. Akan tetapi, S bukan himpunan ortonormal karena norm ‖u2‖ = ‖u3‖ = √2 ≠ 1. Untuk mengubahnya menjadi himpunan ortonormal, bagi masing-masing dengan normnya.
Dalam suatu ruang hasil kali dalam, sebuah basis yang terdiri dari vektor-vektor ortonormal disebut basis ortonormal, dan sebuah basis yang terdiri dari vektor-vektor ortogonal disebut basis ortogonal. Contoh yang familiar dari basis ortonormal adalah basis standar untuk R³ dengan hasil kali dalam Euklidean:
i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)
Ini adalah basis yang terkait dengan sistem koordinat Cartesius. Lebih umum lagi, dalam Rⁿ dengan hasil kali dalam Euklidean, basis standar
e₁ = (1, 0, 0, ..., 0), e₂ = (0, 1, 0, 0), ..., eₙ = (0, 0, 0, ..., 1)
adalah ortonormal.
2. Koordinat Relatif Terhadap Basis Ortonormal
Jika S = {v₁, v₂, ..., vₙ} adalah basis ortonormal untuk ruang hasil kali dalam V, dan u adalah vektor sembarang di V, maka u = 〈u, v₁〉v₁ + 〈u, v₂〉v₂ + ... + 〈u, vₙ〉vₙ.
Perhatikan uraian berikut:
Karena S = {v₁, v₂, ..., vₙ} adalah sebuah basis, maka setiap vektor u dapat dinyatakan dalam bentuk
u = k₁v₁ + k₂v₂ + ... + kₙvₙ
Untuk setiap vektor vᵢ dalam S, kita punya:
〈u, vᵢ〉 = 〈k₁v₁ + k₂v₂ + ... + kₙvₙ, vᵢ〉 = k₁〈v₁, vᵢ〉 + k₂〈v₂, vᵢ〉 + ... + kₙ〈vₙ, vᵢ〉
Karena S = {v₁, v₂, ..., vₙ} adalah himpunan ortonormal, kita punya:
〈vᵢ, vᵢ〉 = ‖vᵢ‖² = 1 dan 〈vⱼ, vᵢ〉 = 0 untuk j ≠ i
Oleh karena itu, persamaan di atas untuk 〈u, vᵢ〉 menjadi:
〈u, vᵢ〉 = kᵢ
Skalar 〈u, v₁〉, 〈u, v₂〉, ..., 〈u, vₙ〉 dalam adalah koordinat dari vektor u relatif terhadap basis ortonormal S = {v₁, v₂, ..., vₙ}, dan
(u)ₛ = (〈u, v₁〉, 〈u, v₂〉, ..., 〈u, vₙ〉)
adalah vektor koordinat dari u relatif terhadap basis ini.
Secara geometri, persamaan ini menyatakan bahwa setiap vektor dalam ruang V dapat diuraikan menjadi komponen-komponen yang sejajar dengan vektor-vektor basis ortonormal. Masing-masing komponen ini merupakan proyeksi ortogonal dari vektor u ke arah vektor basis yang bersesuaian.
Contoh:
Misal v1 = (0, 1, 0), v2 = (−⅘, 0, ⅗), v3 = (⅗, 0, ⅘), himpunan S = {v1, v2, v3} merupakan basis ortonormal untuk R3 karena masing-masing saling tegak lurus dan memiliki norm 1. Nyatakan vektor u = (1, 1, 1) sebagai kombinasi linear dari vektor-vektor di S dan tentukan vektor koordinat (u)ₛ.
〈u, v1〉 = 1, 〈u, v2〉 = −⅕, 〈u, v3〉 = 7/5
sehingga dapat dituliskan (1, 1, 1) = 1(0, 1, 0) − ⅕(−⅘, 0, ⅗) + (7/5)(⅗, 0, ⅘)
vektor koordinat relatif u terhadap S adalah (u)ₛ = (1, −⅕, 7/5)
3. Rumus-Rumus untuk Basis Ortonormal
Misal S basis ortonormal untuk ruang hasil kali dalam berdimensi n, dan diberikan
(u)ₛ = (u₁, u₂, ..., uₙ) dan (v)ₛ = (v₁, v₂, ..., vₙ)
Berikut rumus-rumus terkait basis ortonormal S:
a. Norm vektor
〈u, v〉 = u₁v₁ + u₂v₂ + ... + uₙvₙ
Ingat kembali contoh sebelumnya dimana u = (1, 1, 1) dan (u)ₛ = (1, −⅕, 7/5)
‖u‖² = 1² + 1² + 1² = 3
‖(u)ₛ‖² = 1² + (−⅕)² + (7/5)² = 3
4. Koordinat Relatif Terhadap Basis Ortogonal
Misal S = {v₁, v₂, ..., vₙ} adalah basis ortogonal untuk ruang vektor V, maka dengan menormalkan setiap vektor ini, kita akan mendapatkan basis ortonormal S' sebagai berikut:
Dengan demikian, misal u adalah vektor sembarang di V, kita dapat menyatakan
kita juga dapat menuliskan:
kita juga dapat menuliskan:
Formula ini menyatakan u sebagai kombinasi linear dari vektor-vektor di basis ortogonal S. Koefisien dalam kombinasi linear ini adalah hasil bagi antara hasil kali dalam u dengan masing-masing vektor basis dan kuadrat panjang vektor basis tersebut.
Basis ortonormal memberikan cara yang sangat efisien untuk merepresentasikan vektor-vektor dalam suatu ruang vektor. Setiap vektor dapat dinyatakan secara unik sebagai kombinasi linear dari vektor-vektor dalam basis ortonormal, dan koefisien dalam kombinasi linear ini memiliki interpretasi geometri yang jelas sebagai proyeksi ortogonal.
5. Kebebasan Linear Himpunan Ortogonal
Jika S = {v₁, v₂, ..., vₙ} adalah himpunan ortogonal dari vektor-vektor tak nol dalam suatu ruang hasil kali dalam, maka S bebas linear.
Dengan kata lain, jika kita memiliki sekumpulan vektor yang saling tegak lurus dan tidak ada satupun yang merupakan vektor nol, maka vektor-vektor tersebut pasti bebas linear.
Perhatikan uraian berikut:
Asumsikan bahwa k₁v₁ + k₂v₂ + ... + kₙvₙ = 0.
Untuk setiap vᵢ dalam S, kita dapatkan 〈k₁v₁ + k₂v₂ + ... + kₙvₙ, vᵢ〉 = 〈0, vᵢ〉 = 0, bisa juga dituliskan
k₁〈v₁, vᵢ〉 + k₂〈v₂, vᵢ〉 + ... + kₙ〈vₙ, vᵢ〉 = 0
Karena S adalah himpunan ortogonal, maka (vⱼ, vᵢ) = 0 ketika j ≠ i, sehingga persamaan di atas menjadi
kᵢ〈vᵢ, vᵢ〉 = 0
Karena vektor-vektor dalam S diasumsikan bukan nol, 〈vᵢ, vᵢ〉 ≠ 0 berdasarkan aksioma positifitas untuk hasil kali dalam. Oleh karena itu, kᵢ = 0.
Karena indeks i dipilih sebarang, maka kita memiliki k₁ = k₂ = ... = kₙ = 0; sehingga S bebas linear.
6. Proyeksi Ortogonal
Kita sekarang akan mengembangkan beberapa hasil yang akan membantu kita untuk membangun basis ortonormal dan ortogonal untuk ruang hasil kali dalam. Dalam R² atau R³ dengan hasil kali dalam Euklidean, secara geometris jelas bahwa jika W adalah sebuah garis atau bidang yang melalui asal, maka setiap vektor u dalam ruang dapat dinyatakan sebagai jumlah
u = w₁ + w₂
di mana w₁ berada dalam W dan w₂ tegak lurus terhadap W.
Jika W adalah subruang berdimensi hingga dari suatu ruang hasil kali dalam V, maka setiap vektor u dalam V dapat dinyatakan secara unik sebagai
u = w₁ + w₂
di mana w₁ berada dalam W dan w₂ berada di W⊥ yang tegak lurus terhadap W.
Dinyatakan secara unik artinya setiap vektor u dalam V hanya dapat diuraikan menjadi w₁ dan w₂ dengan cara yang tepat satu. Tidak ada cara lain untuk menguraikan u menjadi dua komponen yang memenuhi syarat tersebut.
Secara geometris, setiap vektor dalam ruang V dapat diproyeksikan secara ortogonal ke subruang W. Vektor w₁ adalah proyeksi ortogonal dari u ke W, dan w₂ adalah komponen yang "tersisa" setelah proyeksi. Bayangkan sebuah ruangan (V) dan sebuah dinding di dalamnya (W). Setiap titik di ruangan (vektor u) dapat diproyeksikan ke dinding (w₁). Jarak tegak lurus dari titik tersebut ke dinding adalah w₂.
Vektor w₁ disebut proyeksi ortogonal dari u pada W dan dinotasikan dengan projW(u). Vektor w₂ disebut komponen dari u yang ortogonal terhadap W dan dinotasikan dengan projW⊥(u). Dengan demikian, formula u = w₁ + w₂ dapat dinyatakan sebagai
u = projW(u) + projW⊥(u)
Karena w₂ = u − w₁, dapat dituliskan
projW⊥(u) = u − projW(u)
Sehingga dapat juga dituliskan
u = projW(u) + [u − projW(u)]
Proyeksi ortogonal dari suatu vektor u pada subruang W adalah vektor w₁ dalam W yang paling dekat dengan u. Komponen w₂ adalah bagian dari vektor u yang tegak lurus terhadap subruang W. Setiap vektor u dapat dinyatakan sebagai jumlah dari proyeksi ortogonalnya pada subruang W dan komponen yang tegak lurus terhadap W.
Bayangkan sebuah ruangan (V) dengan sebuah dinding (W). Jika kita memiliki sebuah bola (vektor u), maka:
projW(u) adalah bayangan bola pada dinding. Ini adalah titik terdekat pada dinding dari pusat bola.
projW⊥(u) adalah vektor yang menghubungkan bayangan bola pada dinding dengan pusat bola. Vektor ini tegak lurus terhadap dinding.
7. Menghitung Proyeksi
Misalkan W adalah subruang berdimensi hingga dari suatu ruang hasil kali dalam V.
(a) Jika {v₁, v₂, ..., vᵣ} adalah basis ortonormal untuk W, dan u adalah sembarang vektor di V, maka
projW(u) = 〈u, v₁〉v₁ + 〈u, v₂〉v₂ + ... + 〈u, vᵣ〉vᵣ
(b) Jika {v₁, v₂, ..., vᵣ} adalah basis ortogonal untuk W, dan u adalah sembarang vektor di V, maka
Kedua persamaan di atas memberikan rumus untuk menghitung proyeksi ortogonal suatu vektor u ke suatu subruang W. Proyeksi ortogonal ini adalah vektor dalam W yang paling dekat dengan vektor u.
Rumus proyeksi untuk basis ortonormal lebih sederhana karena tidak melibatkan pembagian dengan norma kuadrat dari vektor-vektor basis. Sedangkan rumus proyeksi untuk basis ortogonal melibatkan pembagian dengan norma kuadrat dari masing-masing vektor basis untuk menormalkan proyeksi.
Contoh:Misal R3 dengan hasil kali dalam Euclid dan W adalah subruang yang direntang oleh vektor-vektor ortonormal v₁ = (0, 1, 0) dan v₂ = (−⅘, 0, ⅗). Misal u = (1, 1, 1), proyeksi ortogonal u pada W adalah
projW(u) = 〈u, v₁〉v₁ + 〈u, v₂〉v₂ = 1(0, 1, 0) − ⅕(−⅘, 0, ⅗) = (4/25, 1, −3/25)
Komponen u yang ortogonal terhadap W adalah
projW⊥(u) = u − projW(u) = (1, 1, 1) − (4/25, 1, −3/25) = (21/25, 0, 28/25)
Amati bahwa projW⊥(u) ortogonal terhadap v₁ maupun v₂, vektor ini ortogonal terhadap vektor di ruang W yang direntang oleh v₁ dan v₂ sebagaimana mestinya.
8. Menemukan Basis Ortogonal dan Ortonormal
Setiap ruang hasil kali dalam berdimensi hingga yang bukan nol memiliki basis ortonormal.
Misalkan V adalah ruang hasil kali dalam berdimensi hingga yang bukan nol, dan misalkan {u₁, u₂, ..., uₙ} adalah sembarang basis untuk V. Cukup untuk menunjukkan bahwa V memiliki basis ortogonal, karena vektor-vektor dalam basis ortogonal dapat dinormalisasi untuk menghasilkan basis ortonormal untuk V. Urutan langkah berikut akan menghasilkan basis ortogonal {v₁, v₂, ..., vₙ} untuk V.
Setiap ruang vektor yang memenuhi berdimensi hingga, bukan nol, dan memiliki hasil kali dalam pasti memiliki sekumpulan vektor yang bisa dijadikan sebagai basis untuk ruang tersebut. Selain itu, vektor-vektor dalam basis ini memiliki sifat khusus: saling tegak lurus dan memiliki panjang 1.
Bayangkan sebuah ruangan (ruang vektor). Kita bisa memilih berbagai cara untuk mendeskripsikan posisi suatu titik di ruangan tersebut (basis). Namun, basis ortonormal adalah seperti memilih tiga sumbu koordinat yang saling tegak lurus dan memiliki panjang yang sama. Ini adalah cara yang paling sederhana dan intuitif untuk mendeskripsikan posisi suatu titik. Ini memberikan kita jaminan bahwa kita selalu dapat menemukan basis ortonormal untuk setiap ruang hasil kali dalam berdimensi hingga.
9. Proses Gram-Schmidt
A. Misalkan v₁ = u₁.
Langkah ini sangat sederhana. Vektor pertama dalam basis ortonormal baru kita, v₁, langsung diambil dari vektor pertama dalam basis awal, u₁. Ini menjadi titik awal untuk membangun basis ortonormal yang baru.
B. Kita dapat memperoleh vektor v₂ yang ortogonal terhadap v₁ dengan menghitung komponen dari u₂ yang ortogonal terhadap ruang W₁ yang direntang oleh v₁.
Vektor v₂ diperoleh dengan mengurangi proyeksi ortogonal dari u₂ ke v₁ dari u₂ sendiri. Kita gunakan rumus:
Formula ini secara matematis menyatakan bagaimana kita menghitung v₂. Kita mengambil vektor u₂, lalu kita kurangi proyeksi ortogonal dari u₂ ke ruang yang direntang oleh v₁. Proyeksi ortogonal ini dihitung dengan mengalikan hasil kali dalam antara u₂ dan v₁ dengan v₁ yang dinormalisasi (dibagi dengan norm kuadratnya).
Jika v₂ ternyata nol, maka v₂ tidak bisa menjadi bagian dari basis. Namun, ini tidak mungkin terjadi karena dari persamaan v₂ kita bisa melihat bahwa jika v₂ adalah nol, maka u₂ akan menjadi kelipatan dari v₁, yang bertentangan dengan asumsi bahwa {u₁, u₂, ..., uₙ} adalah basis (semua vektor dalam basis harus bebas linear).
Jika v₂ ternyata nol, maka v₂ tidak bisa menjadi bagian dari basis. Namun, ini tidak mungkin terjadi karena dari persamaan v₂ kita bisa melihat bahwa jika v₂ adalah nol, maka u₂ akan menjadi kelipatan dari v₁, yang bertentangan dengan asumsi bahwa {u₁, u₂, ..., uₙ} adalah basis (semua vektor dalam basis harus bebas linear).
Setelah mendapatkan v₁, kita akan melanjutkan dengan mencari v₃ yang ortogonal terhadap v₁ dan v₂, dan seterusnya, hingga kita mendapatkan seluruh basis ortonormal {v₁, v₂, ..., vₙ}. Proses ini memastikan bahwa setiap vektor dalam basis baru saling tegak lurus dan tidak ada vektor yang dapat dinyatakan sebagai kombinasi linear dari vektor-vektor lainnya.
Contoh:
Misal R3 dengan hasil kali dalam Euclid. Gunakan proses Gram-Schmidt untuk mentransformasikan vektor-vektor basis u1 = (1, 1, 1), u2 = (0, 1, 1), u3 = (0, 0, 1) ke basis ortogonal {v1, v2, v3}; lalu normalisasi ke basis ortonormal {q1, q2, q3}.
Langkah 1
Misal v1 = u1 = (1, 1, 1)
Langkah 2
Lakukan normalisasi, akan diperoleh:
Catatan: Pada contoh sebelumnya, kita menggunakan proses Gram-Schmidt untuk menghasilkan basis ortogonal, kemudian setelah seluruh basis ortogonal diperoleh, kita menormalisasi untuk mendapatkan basis ortonormal. Alternatifnya, seseorang dapat menormalisasi setiap vektor basis ortogonal segera setelah diperoleh, sehingga menghasilkan basis ortonormal langkah demi langkah. Namun, metode ini memiliki sedikit kelemahan yaitu menghasilkan lebih banyak akar kuadrat untuk dimanipulasi.
Proses Gram-Schmidt dengan normalisasi selanjutnya tidak hanya mengubah basis sembarang (u₁, u₂, ..., uₙ) menjadi basis ortonormal (q₁, q₂, ..., qₙ) tetapi juga melakukannya sedemikian rupa sehingga untuk k ≥ 2 hubungan berikut berlaku:
• (q₁, q₂, ..., qₖ) adalah basis ortonormal untuk ruang yang direntang oleh (u₁, u₂, ..., uₖ).
• qₖ adalah ortogonal terhadap ruang yang direntang oleh (u₁, u₂, ..., uₖ₋₁).
10. Dekomposisi QR
Masalah: Jika A adalah matriks m × n dengan vektor kolom yang saling bebas secara linear, dan jika Q adalah matriks dengan vektor kolom ortonormal yang dihasilkan dari penerapan proses Gram-Schmidt pada vektor kolom A, hubungan apa, jika ada, yang ada antara A dan Q?
Untuk menyelesaikan masalah ini, anggaplah bahwa vektor kolom A adalah u₁, u₂, ..., uₙ, dan vektor kolom ortonormal dari Q adalah q₁, q₂, ..., qₙ. Dengan demikian:
A = [u₁ u₂ ... uₙ] dan Q = [q₁ q₂ ... qₙ]
Kita dapat menyatakan u₁, u₂, ..., uₙ dalam bentuk vektor q₁, q₂, ..., qₙ sebagai:
u₁ = 〈u₁, q₁〉q₁ + 〈u₁, q₂〉q₂ + ... + 〈u₁, qₙ〉qₙ
u₂ = 〈u₂, q₁〉q₁ + 〈u₂, q₂〉q₂ + ... + 〈u₂, qₙ〉qₙ
...
uₙ = 〈uₙ, q₁〉q₁ + 〈uₙ, q₂〉q₂ + ... + 〈uₙ, qₙ〉qₙ
Kolom ke-j dari hasil kali matriks adalah kombinasi linear dari kolom-kolom matriks pertama dengan koefisien yang berasal dari kolom ke-j dari matriks kedua, maka hubungan-hubungan ini dapat dinyatakan dalam bentuk matriks sebagai:
atau lebih singkat sebagai:
A = QR
Namun, merupakan sifat dari proses Gram-Schmidt bahwa untuk j ≥ 2, vektor qⱼ ortogonal terhadap u₁, u₂, ..., uⱼ₋₁; sehingga, semua entri di bawah diagonal utama R adalah nol.
Proses Gram-Schmidt memastikan bahwa setiap vektor qⱼ yang dihasilkan ortogonal terhadap semua vektor sebelumnya (u₁, u₂, ..., uⱼ₋₁). Akibatnya, ketika kita menghitung hasil kali dalam antara uᵢ dan qⱼ dengan i < j, hasilnya akan selalu nol. Ini menjelaskan mengapa semua entri di bawah diagonal utama matriks R adalah nol.
Bentuk A = QR adalah faktorisasi dari A menjadi hasil kali matriks Q dengan vektor kolom ortonormal dan matriks segitiga atas yang dapat dibalik R. Persamaan A = QR disebut sebagai dekomposisi QR. Ini adalah cara untuk menyatakan matriks A sebagai hasil kali dari matriks Q (matriks ortogonal) dan matriks R (matriks segitiga atas yang dapat dibalik).
Rangkuman:
Jika A adalah matriks m × n dengan vektor kolom yang saling bebas secara linear, maka A dapat difaktorkan sebagai:
A = QR
di mana Q adalah matriks m × n dengan vektor kolom ortonormal, dan R adalah matriks n × n segitiga atas yang dapat dibalik.
Catatan: Ingat kembali bahwa jika A adalah matriks n × n, maka dapat dibalik jika dan hanya jika vektor kolomnya saling bebas secara linear; dengan demikian, setiap matriks yang dapat dibalik memiliki dekomposisi QR.
Penjelasan:
• Matriks A: Matriks awal yang memiliki vektor kolom yang saling bebas secara linear. Ini berarti tidak ada vektor kolom dalam A yang dapat dinyatakan sebagai kombinasi linear dari vektor kolom lainnya.
• Matriks Q: Matriks ini memiliki dimensi yang sama dengan A, yaitu m × n. Kolom-kolom dalam Q saling tegak lurus (ortonormal). Ini berarti panjang setiap vektor kolom adalah 1 dan setiap pasangan vektor kolom membentuk sudut 90 derajat.
• Matriks R: Matriks ini berukuran n × n dan berbentuk segitiga atas. Ini berarti semua elemen di bawah diagonal utama adalah nol. Selain itu, matriks R dapat dibalik, artinya ada matriks invers R⁻¹ yang jika dikalikan dengan R menghasilkan matriks identitas.
• Hubungan A, Q, dan R: Persamaan A = QR menunjukkan bahwa matriks A dapat diperoleh dengan mengalikan matriks Q dengan matriks R. Ini berarti informasi tentang matriks A tersimpan dalam kedua matriks ini.
Tambahan:
• Jika semua vektor kolom dalam sebuah matriks saling bebas secara linear, maka matriks tersebut dapat dibalik dan sebaliknya.
• Setiap matriks yang dapat dibalik memiliki dekomposisi QR. Jika sebuah matriks dapat dibalik, maka kita dapat melakukan proses Gram-Schmidt untuk mendapatkan matriks Q dengan kolom-kolom ortonormal. Kemudian, kita dapat menghitung matriks R dengan mengalikan invers dari Q dengan A.
Contoh:
Tentukan dekomposisi QR dari matriks
Dalam beberapa tahun terakhir, dekomposisi QR telah dianggap semakin penting sebagai fondasi matematis untuk berbagai macam algoritma numerik praktis, termasuk algoritma yang banyak digunakan untuk menghitung nilai eigen dari matriks besar. Algoritma semacam itu dibahas dalam buku-buku teks yang membahas aljabar linear numerik.
Dekomposisi QR ini ternyata sangat berguna sebagai dasar untuk membangun berbagai algoritma yang digunakan untuk menyelesaikan masalah-masalah numerik, seperti:
• Menghitung nilai eigen dari matriks besar: Nilai eigen adalah nilai skalar yang terkait dengan suatu transformasi linear dan sering digunakan dalam berbagai bidang seperti fisika, teknik, dan ekonomi.
• Memecahkan sistem persamaan linear: Dekomposisi QR dapat digunakan untuk menyelesaikan sistem persamaan linear secara lebih efisien dan stabil.
• Regresi linear: Dekomposisi QR dapat digunakan untuk menghitung koefisien regresi.








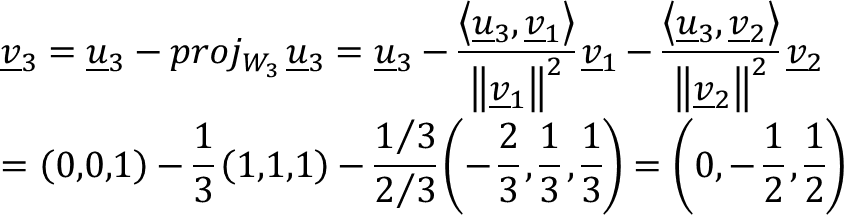

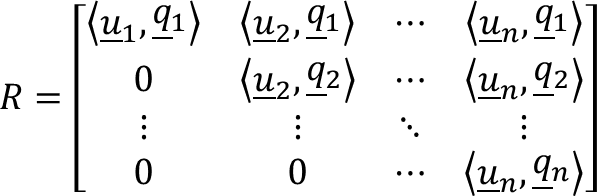







Komentar
Posting Komentar