Nilai Eigen dan Vektor Eigen
1. Nilai Eigen dan Vektor Eigen
Misal matriks A berukuran n × n, vektor taknol x di Rn disebut sebagai vektor eigen dari A jika Ax sama dengan kelipatan dari x, misalnya Ax = λx untuk suatu skalar λ. Skalar λ disebut sebagai nilai eigen dari A, sedang x disebut vektor eigen dari A yang bersesuaian dengan λ.
2. Menentukan Nilai Eigen
Untuk menentukan nilai eigen dari sebuah matriks A berukuran n × n, kita tulis ulang Ax = λx sebagai:
λIx = Ax, kurangi masing-masing ruas dengan Ax
(λI − A)x = 0, terbentuk SPL homogen
Agar λ menjadi nilai eigen, harus ada solusi non-trivial untuk SPL ini. Ingat kembali bahwa SPL homogen memiliki solusi non-trivial jika dan hanya jika determinan matriks koefisien adalah nol.
det(λI − A) = 0
Persamaan ini disebut persamaan karakteristik dari A. Skalar yang memenuhi persamaan ini adalah nilai eigen dari A. Ketika dijabarkan, determinan det(λI − A) selalu merupakan polinomial p dalam λ, yang disebut polinomial karakteristik dari A.
Karena A matriks n × n, polinomial karakteristik dari A memiliki derajat n dan koefisien dari λn adalah 1; dengan kata lain, polinomial karakteristik dari matriks n × n memiliki bentuk:
p(λ) = det(λI − A) = λn + c1λn-1 + c2λn-2 + ... + cn
Dari Teorema Dasar Aljabar, mengikuti bahwa persamaan karakteristik:
λn + c1λn-1 + c2λn-2 + ... + cn = 0
memiliki paling banyak n solusi berbeda, sehingga sebuah matriks n × n memiliki paling banyak n nilai eigen berbeda.
Contoh:
nilai eigennya adalah λ = −1 ∨ λ = 6.
3. Kasus Khusus untuk Matriks Segitiga
Nilai eigen dari matriks segitiga adalah entri-entri pada diagonal utama.
Ingat kembali bahwa determinan matriks segitiga adalah hasil kali entri-entri diagonal utama, agar determinannya nol, diperlukan adanya elemen 0 pada diagonal utama, sehingga nilai eigennya adalah entri-entri pada diagonal utama.
4. Menentukan Vektor Eigen dan Basis untuk Ruang Eigen
Vektor eigen dari A yang bersesuaian dengan nilai eigen λ adalah vektor-vektor taknol x yang memenuhi Ax = λx. Dengan kata lain, vektor eigen yang bersesuaian dengan λ adalah vektor-vektor taknol dalam ruang solusi dari (λI − A)x = 0, yaitu dalam ruang null dari (λI − A). Kita menyebut ruang solusi ini sebagai ruang eigen dari A yang bersesuaian dengan λ.
Contoh:
λ = −1 ∨ λ = 1 ∨ λ = 2
Untuk λ = −1, terbentuk SPL homogen:
Untuk λ = 1, terbentuk SPL homogen:
5. Nilai Eigen Perpangkatan Matriks
Setelah nilai eigen dan vektor eigen dari suatu matriks A ditemukan, sangat mudah untuk menemukan nilai eigen dan vektor eigen dari setiap pangkat bilangan bulat positif dari A; misalnya, jika λ adalah nilai eigen dari A dan x adalah vektor eigen yang bersesuaian, maka
A²x = A(Ax) = A(λx) = λ(Ax) = λ(λx) = λ²x
yang menunjukkan bahwa λ² adalah nilai eigen dari A² dan x adalah vektor eigen yang bersesuaian. Secara umum, kita memiliki hasil sebagai berikut:
"Jika k adalah bilangan bulat positif, λ adalah nilai eigen dari suatu matriks A, dan x adalah vektor eigen yang bersesuaian, maka λk adalah nilai eigen dari Ak dan x adalah vektor eigen yang bersesuaian."
6. Invertibilitas
Matriks persegi A dapat dibalik jika dan hanya jika λ = 0 bukan nilai eigen dari A.
Bukti:
Misal A adalah matriks berukuran n × n dan perhatikan bahwa λ = 0 adalah solusi dari persamaan karakteristik
λn + c1λn-1 + c2λn-2 + ... + cn = 0
jika dan hanya jika konstanta terakhir, cₙ, sama dengan nol. Dengan demikian, cukup untuk membuktikan bahwa A dapat dibalik jika dan hanya jika cₙ ≠ 0. Tetapi,
det(λI − A) = λn + c1λn-1 + c2λn-2 + ... + cn
atau, dengan mensubstitusikan λ = 0,
det(−A) = cₙ atau (−1)n.det(A) = cₙ
Dari persamaan terakhir, dapat disimpulkan bahwa det(A) = 0 jika dan hanya jika cₙ = 0, dan ini pada gilirannya menyiratkan bahwa A dapat dibalik jika dan hanya jika cₙ ≠ 0.


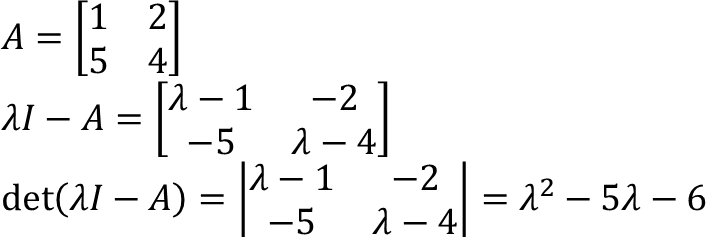





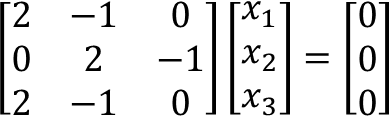



Komentar
Posting Komentar