Transformasi Linear dari Rn ke Rm

1. Fungsi dari Rn ke Rm

Jika domain dari suatu fungsi f adalah ℝⁿ dan kodomainnya adalah ℝᵐ (m dan n mungkin sama), maka f disebut pemetaan atau transformasi dari ℝⁿ ke ℝᵐ, dan kita katakan bahwa fungsi f memetakan ℝⁿ ke dalam ℝᵐ. Kita menotasikan ini dengan menulis 𝑓: ℝⁿ → ℝᵐ. Dalam kasus di mana m = n, transformasi 𝑓: ℝⁿ → ℝⁿ disebut operator pada ℝⁿ.

Untuk mengilustrasikan salah satu cara penting di mana transformasi dapat muncul, misalkan 𝑓₁, 𝑓₂, ..., 𝑓ₘ adalah fungsi-fungsi bernilai real dari n variabel real, katakanlah:

𝑤₁ = 𝑓₁(𝑥₁, 𝑥₂, ..., 𝑥ₙ)

𝑤₂ = 𝑓₂(𝑥₁, 𝑥₂, ..., 𝑥ₙ)

⋮

𝑤ₘ = 𝑓ₘ(𝑥₁, 𝑥₂, ..., 𝑥ₙ)

Persamaan-persamaan ini memberikan suatu titik tunggal (𝑤₁, 𝑤₂, ..., 𝑤ₘ) di ℝᵐ untuk setiap titik (𝑥₁, 𝑥₂, ..., 𝑥ₙ) di ℝⁿ dan dengan demikian mendefinisikan suatu transformasi dari ℝⁿ ke ℝᵐ. Jika kita notasikan transformasi ini dengan T, maka 𝑇: ℝⁿ → ℝᵐ dan

𝑇(𝑥₁, 𝑥₂, ..., 𝑥ₙ) = (𝑤₁, 𝑤₂, ..., 𝑤ₘ).

Sebagai contoh, fungsi dua variabel merupakan transformasi dari R2 ke R1, fungsi kurva bidang merupakan transformasi dari R1 ke R2, fungsi kurva ruang merupakan transformasi dari R1 ke R3.

2. Transformasi Linear dari Rn ke Rm

Dalam kasus khusus dimana transformasi dari Rn ke Rm bersifat linear, transformasi 𝑇: ℝⁿ → ℝᵐ yang didefinisikan oleh persamaan-persamaan tersebut disebut transformasi linear (atau operator linear jika m = n). Dengan demikian, suatu transformasi linear 𝑇: ℝⁿ → ℝᵐ didefinisikan oleh persamaan-persamaan dalam bentuk:

𝑤₁ = 𝑎₁₁𝑥₁ + 𝑎₁₂𝑥₂ + ... + 𝑎₁ₙ𝑥ₙ

𝑤₂ = 𝑎₂₁𝑥₁ + 𝑎₂₂𝑥₂ + ... + 𝑎₂ₙ𝑥ₙ

⋮

𝑤ₘ = 𝑎ₘ₁𝑥₁ + 𝑎ₘ₂𝑥₂ + ... + 𝑎ₘₙ𝑥ₙ

atau, dalam notasi matriks,

atau lebih singkat dengan

𝑤 = 𝐴𝑥 

Matriks 𝐴 = [𝑎ᵢⱼ] disebut matriks standar untuk transformasi linear T, dan T disebut perkalian dengan A.

Contoh: Transformasi linear dari R3 ke R2

Misal diberikan matriks transformasi sebagai berikut:

Terapkan transformasi linear ini pada x = (7, 8, 9)

Hasil transformasinya adalah w = (50, 122)

3. Notasi untuk Transformasi Linear

Jika 𝑇: ℝⁿ → ℝᵐ adalah perkalian dengan A, dan jika penting untuk menekankan bahwa A adalah matriks standar untuk T, maka kita akan menotasikan transformasi linear 𝑇: ℝⁿ → ℝᵐ dengan 𝑇_A: ℝⁿ → ℝᵐ. Dengan demikian,

𝑇_A(𝑥) = 𝐴𝑥 

Dalam persamaan ini, vektor 𝑥 di ℝⁿ dinyatakan sebagai matriks kolom.

Terkadang, agak rumit untuk memperkenalkan huruf baru untuk menotasikan matriks standar dari suatu transformasi linear 𝑇: ℝⁿ → ℝᵐ. Dalam kasus seperti itu, kita akan menotasikan matriks standar untuk T dengan simbol [𝑇]. Dengan notasi ini, persamaannya akan berbentuk

𝑇(𝑥) = [𝑇]𝑥 

Terkadang, kedua notasi untuk matriks standar akan dicampur, dalam hal ini kita memiliki hubungan

[𝑇_A] = 𝐴

Catatan: Di tengah semua notasi ini, penting untuk diingat bahwa kita telah membangun suatu korespondensi antara matriks 𝑚 × 𝑛 dan transformasi linear dari ℝⁿ ke ℝᵐ: Untuk setiap matriks A, terdapat suatu transformasi linear 𝑇_A (perkalian dengan A), dan untuk setiap transformasi linear 𝑇: ℝⁿ → ℝᵐ, terdapat suatu matriks 𝑚 × 𝑛 [𝑇] (matriks standar untuk T).

4. Interpretasi Geometri dari Transformasi Linear

Tergantung pada apakah n-tuple dianggap sebagai titik atau vektor, efek geometri dari suatu operator T: ℝⁿ → ℝⁿ adalah untuk mengubah setiap titik (atau vektor) di ℝⁿ menjadi titik baru (atau vektor).

5. Transformasi Nol dari Rn ke Rm

Jika O adalah matriks nol berukuran m × n dan 0 adalah vektor nol di ℝⁿ, maka untuk setiap vektor x di ℝⁿ,

T₀(x) = Ox = 0 

sehingga perkalian dengan matriks nol memetakan setiap vektor di ℝⁿ ke vektor nol di ℝᵐ. Kita menyebut T₀ sebagai transformasi nol dari ℝⁿ ke ℝᵐ. Kadang-kadang transformasi nol dinotasikan dengan 0. Meskipun ini adalah notasi yang sama yang digunakan untuk matriks nol, interpretasi yang tepat biasanya akan jelas dari konteksnya.

6. Operator Identitas di Rn

Jika I adalah matriks identitas berukuran n × n, maka untuk setiap vektor x di ℝⁿ,

T_I(x) = Ix = x 

sehingga perkalian dengan I memetakan setiap vektor di ℝⁿ ke dirinya sendiri. Kita menyebut T_I sebagai operator identitas pada ℝⁿ. Kadang-kadang operator identitas dinotasikan dengan I. Meskipun ini adalah notasi yang sama yang digunakan untuk matriks identitas, interpretasi yang tepat biasanya akan jelas dari konteksnya.

7. Operator Rotasi

Di antara operator linear yang paling penting pada ℝ² dan ℝ³ adalah yang menghasilkan refleksi, proyeksi, dan rotasi. Kita akan membahas operator rotasi tersebut pada poin ini.

Suatu operator yang memutar setiap vektor di ℝ² melalui sudut tetap θ disebut operator rotasi pada ℝ². Untuk mengetahui bagaimana rumus rotasi diperoleh, perhatikan operator rotasi yang memutar setiap vektor berlawanan arah jarum jam melalui sudut tetap positif θ. Untuk menemukan persamaan yang menghubungkan x dan w = T(x), misalkan θ adalah sudut dari sumbu x positif ke x, dan misalkan r adalah panjang yang sama dari x dan w.

Dari trigonometri dasar, kita dapatkan:

x = r.cos(φ), y = r.sin(φ) 

dan

w₁ = r.cos(θ + φ), w₂ = r.sin(θ + φ) 

Dengan menggunakan identitas trigonometri, kita peroleh:

w₁ = r.cos(θ).cos(φ) – r.sin(θ).sin(φ)

w₂ = r.sin(θ).cos(φ) + r.cos(θ).sin(φ)

dan dengan mensubstitusikan x dan y, kita dapatkan:

w₁ = x.cos(θ) – y.sin(θ)

w₂ = x.sin(θ) + y.cos(θ) 

Persamaan ini bersifat linear, sehingga T adalah operator linear. Lebih lanjut, dari persamaan-persamaan ini, kita dapat menyimpulkan bahwa matriks standar untuk T adalah

8. Yaw, Pitch, dan Roll

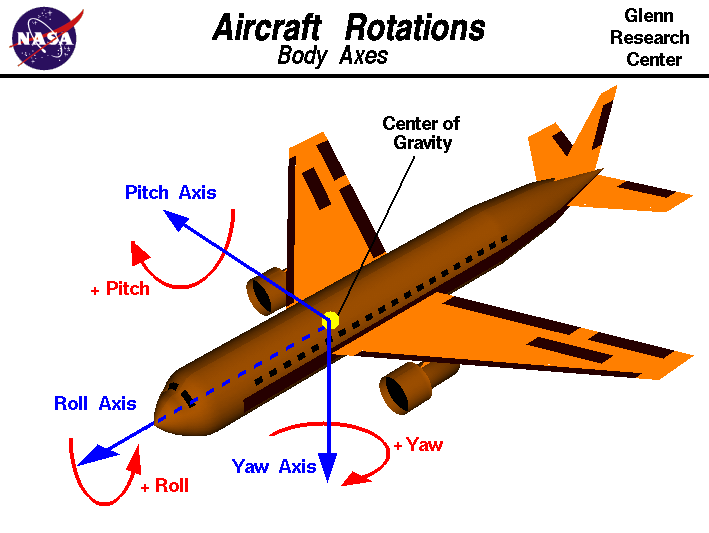
Dalam bidang aeronautika dan astronautika, orientasi suatu pesawat terbang atau pesawat ulang-alik relatif terhadap suatu sistem koordinat xyz seringkali dijelaskan dalam bentuk sudut yang disebut yaw, pitch, dan roll. Sebagai contoh, jika sebuah pesawat terbang bergerak sepanjang sumbu y dan bidang XOY mendefinisikan horisontal, maka sudut rotasi pesawat terhadap sumbu z disebut yaw, sudut rotasi terhadap sumbu x disebut pitch, dan sudut rotasi terhadap sumbu y disebut roll.

Kombinasi yaw, pitch, dan roll dapat dicapai melalui satu kali rotasi tunggal terhadap suatu sumbu yang melewati titik asal. Faktanya, inilah cara pesawat ulang-alik melakukan penyesuaian sikap – ia tidak melakukan setiap rotasi secara terpisah; ia menghitung satu sumbu, lalu berotasi terhadap sumbu tersebut untuk mendapatkan orientasi yang benar. Manuver rotasi seperti ini digunakan untuk menyelaraskan antena, mengarahkan hidung ke arah objek langit, atau memposisikan ruang muatan untuk docking.

Untuk melengkapi, kami catat bahwa matriks standar untuk rotasi berlawanan arah jarum jam sebesar sudut θ terhadap sumbu di R³ yang ditentukan oleh vektor satuan sembarang n = (a, b, c) dengan titik pangkal di O adalah:

9. Komposisi Transformasi Linear

Jika T_A: ℝⁿ → ℝᵏ dan T_B: ℝᵏ → ℝᵐ adalah transformasi linear, maka untuk setiap x di ℝⁿ, seseorang dapat pertama-tama menghitung T_A(x), yang merupakan vektor di ℝᵏ, dan kemudian seseorang dapat menghitung T_B(T_A(x)), yang merupakan vektor di ℝᵐ. Dengan demikian, penerapan T_A diikuti oleh T_B menghasilkan transformasi dari ℝⁿ ke ℝᵐ. Transformasi ini disebut komposisi dari T_B dengan T_A dan dinotasikan dengan T_B ∘ T_A (baca "T_B bundaran T_A"). Dengan demikian,

(T_B ∘ T_A)(x) = T_B(T_A(x))

Komposisi T_B ∘ T_A adalah linear karena

(T_B ∘ T_A)(x) = T_B(T_A(x)) = B(Ax) = BAx 

Jadi, T_B ∘ T_A adalah perkalian dengan BA, yang merupakan transformasi linear. Formula ini juga memberi tahu kita bahwa matriks standar untuk T_B ∘ T_A adalah BA. Ini dinyatakan oleh rumus

T_B ∘ T_A = T_BA 

Mengalikan matriks setara dengan mengkomposisikan transformasi linear yang sesuai dalam urutan kanan-ke-kiri dari faktor-faktornya.

Ada bentuk alternatif: Jika T₁: ℝⁿ → ℝᵏ dan T₂: ℝᵏ → ℝᵐ adalah transformasi linear, maka karena matriks standar untuk komposisi T₂ ∘ T₁ adalah hasil kali dari matriks standar T₂ dan T₁, kita memiliki

[T₂ ∘ T₁] = [T₂][T₁]

Perlu diketahui bahwa komposisi transformasi linear tidak komutatif, karena perkalian matriks tidak komutatif.

Transformasi linear bersifat asosiatif karena perkalian matriks bersifat asosiatif.