Transformasi Linear Satu-Satu, Sifat Linear, Matriks Standar
1. Transformasi Linear Satu-Satu
Transformasi linear T: ℝⁿ → ℝᵐ dikatakan satu-satu jika T memetakan vektor (atau titik) yang berbeda di ℝⁿ ke vektor (atau titik) yang berbeda di ℝᵐ.
Catatan: Dari definisi ini, kita dapat menyimpulkan bahwa untuk setiap vektor w dalam range (jangkauan) dari suatu transformasi linear satu-satu T, terdapat tepat satu vektor x sedemikian sehingga T(x) = w.
Transformasi linear yang memetakan vektor (atau titik) yang berbeda ke vektor (atau titik) yang berbeda memiliki kepentingan khusus. Salah satu contoh transformasi seperti itu adalah operator linear T: ℝ² → ℝ² yang merotasi setiap vektor melalui sudut θ. Secara geometris jelas bahwa jika u dan v adalah vektor berbeda di ℝ², maka vektor yang dirotasi T(u) dan T(v) juga berbeda.
2. Pernyataan yang Ekivalen
Misalkan A adalah matriks berukuran n × n, dan kita definisikan transformasi linear TA: ℝⁿ → ℝⁿ sebagai perkalian dengan A. Kita akan menyelidiki hubungan antara invertibilitas matriks A dan sifat-sifat transformasi linear TA.
Ingat kembali (dengan w menggantikan b) bahwa pernyataan berikut ini ekivalen:
• A dapat dibalik (invertible).
• Sistem persamaan linear Ax = w konsisten untuk setiap matriks w berukuran n × 1.
• Sistem persamaan linear Ax = w memiliki tepat satu solusi untuk setiap matriks w berukuran n × 1.
Namun, pernyataan terakhir sebenarnya lebih kuat daripada yang diperlukan, sehingga pernyataan berikut juga ekuivalen:
• A dapat dibalik (invertible).
• Sistem persamaan linear Ax = w konsisten untuk setiap matriks w berukuran n × 1.
• Sistem persamaan linear Ax = w memiliki tepat satu solusi ketika sistem tersebut konsisten.
Dengan menerjemahkan pernyataan-pernyataan ini ke dalam pernyataan yang setara tentang operator linear TA, kita dapat menyimpulkan bahwa pernyataan-pernyataan berikut ini ekuivalen:
• A dapat dibalik.
• Untuk setiap vektor w di ℝⁿ, terdapat suatu vektor x di ℝⁿ sedemikian sehingga TA(x) = w. Dengan kata lain, range dari TA adalah seluruh ℝⁿ.
• Untuk setiap vektor w dalam range dari TA, terdapat tepat satu vektor x di ℝⁿ sedemikian sehingga TA(x) = w. Dengan kata lain, TA adalah satu-satu.
Hal ini dapat dirangkum menjadi:
Misal A adalah matriks berukuran n × n dan TA: ℝⁿ → ℝⁿ adalah transformasi yang didefinisikan sebagai perkalian dengan A, pernyataan-pernyataan berikut ini ekuivalen:
(a) A dapat dibalik (invertible).
(b) Range dari TA adalah seluruh ℝⁿ.
(c) TA adalah satu-satu.
3. Invers Operator Linear Satu-Satu
Misal TA: ℝⁿ → ℝⁿ adalah operator linear satu-satu, matriks A dapat dibalik. Dengan demikian, TA⁻¹: ℝⁿ → ℝⁿ juga merupakan operator linear; ini disebut invers dari TA. Operator linear TA dan TA⁻¹ saling meniadakan efek satu sama lain dalam arti untuk setiap x di ℝⁿ,
TA(TA⁻¹(x)) = AA⁻¹x = Ix = x
dan
TA⁻¹(TA(x)) = A⁻¹Ax = Ix = x
atau, ekivalen,
TA o TA⁻¹ = TA⁻¹ o TA = I
Dari sudut pandang geometri, jika w adalah hasil transformasi TA dari x, maka TA⁻¹ memetakan w kembali ke x, karena
TA⁻¹(w) = TA⁻¹(TA(x)) = x
Kita bahas sedikit mengenai notasi. Ketika operator linear satu-satu pada ℝⁿ ditulis sebagai T: ℝⁿ → ℝⁿ (bukan TA: ℝⁿ → ℝⁿ), maka invers dari operator T dinotasikan dengan T⁻¹ (bukan TA⁻¹). Karena matriks standar untuk T⁻¹ adalah invers dari matriks standar untuk T, kita memiliki
[T⁻¹] = [T]⁻¹
Contoh: Diberikan transformasi linear berikut:
4. Sifat Linearitas
Suatu transformasi T: ℝⁿ → ℝᵐ adalah linear jika dan hanya jika hubungan berikut berlaku untuk semua vektor u dan v di ℝⁿ dan untuk setiap skalar c:
(a) Sifat Aditif
T(u + v) = T(u) + T(v)
T(u + v) = A(u + v) = Au + Av = T(u) + T(v)
(b) Sifat Homogen
T(cu) = cT(u)
T(cu) = A(cu) = c(Au) = cT(u)
Perluasan untuk poin (a):
Secara lebih umum, untuk setiap vektor v₁, v₂, ..., vₖ di ℝⁿ, kita memiliki:
T(v₁ + v₂ + ... + vₖ) = T(v₁) + T(v₂) + ... + T(vₖ)
Sekarang, untuk menemukan matriks A, misalkan e₁, e₂, ..., eₙ adalah vektor-vektor:
dan misalkan A adalah matriks yang kolom-kolomnya berturut-turut adalah T(e₁), T(e₂), ..., T(eₙ), yaitu:
A = [T(e₁) | T(e₂) | ... | T(eₙ)]
Misal
adalah sembarang vektor di ℝⁿ, hasil kali Ax adalah kombinasi linear dari kolom-kolom A dengan koefisien dari x, sehingga:
Ax = x₁T(e₁) + x₂T(e₂) + ... + xₙT(eₙ)
= T(x₁e₁) + T(x₂e₂) + ... + T(xₙeₙ)
= T(x₁e₁ + x₂e₂ + ... + xₙeₙ)
= T(x)
Rangkuman:
Jika T: ℝⁿ → ℝᵐ adalah transformasi linear, dan e₁, e₂, ..., eₙ adalah vektor basis standar untuk ℝⁿ, maka matriks standar untuk T adalah [T] = [T(e₁) | T(e₂) | ... | T(eₙ)]
5. Matriks Standar untuk Operator Proyeksi
Misalkan l adalah garis pada ℝ² yang melalui titik O dan membentuk sudut θ dengan sumbu x positif, di mana 0 ≤ θ < π. Misalkan T: ℝ² → ℝ² adalah operator linear yang memetakan setiap vektor ke proyeksi ortogonalnya pada l.
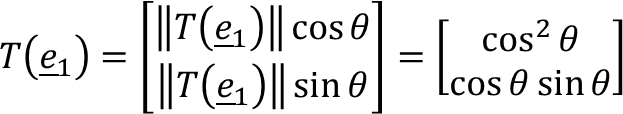
Komentar
Posting Komentar