Transformasi Linear Umum
1. Definisi
Jika T: V → W adalah suatu fungsi dari ruang vektor V ke ruang vektor W, maka T disebut transformasi linear dari V ke W jika untuk setiap vektor u dan v di V dan semua skalar c:
(a) T(u + v) = T(u) + T(v)
(b) T(cu) = cT(u)
Dalam kasus khusus di mana V = W, transformasi linear T: V → V disebut operator linear pada V.
2. Transformasi Matriks, Transformasi Nol, Operator Identitas
A. Transformasi Matriks
Kita akan menyebut transformasi linear dari ℝⁿ ke ℝᵐ sebagai transformasi matriks, karena dapat dilakukan dengan perkalian matriks.
B. Transformasi Nol
Misalkan V dan W adalah dua ruang vektor sembarang. Pemetaan T: V → W sedemikian sehingga T(v) = 0 untuk setiap v di V adalah transformasi linear yang disebut transformasi nol. Untuk melihat bahwa T adalah linear, perhatikan bahwa
T(u + v) = 0, T(u) = 0, T(v) = 0, dan T(ku) = 0
Oleh karena itu,
T(u + v) = T(u) + T(v) dan T(ku) = kT(u)
C. Operator Identitas
Misalkan V adalah sembarang ruang vektor. Pemetaan T: V → V yang didefinisikan oleh T(v) = v untuk setiap v di V disebut operator identitas pada V.
3. Proyeksi Ortogonal
Proyeksi ortogonal dapat didefinisikan pada ruang hasil kali dalam secara umum. Misalkan W adalah subruang berdimensi hingga dari suatu ruang hasil kali dalam V, maka proyeksi ortogonal V ke W adalah transformasi yang didefinisikan oleh
T(v) = projW(v)
T(v) = projW(v) = 〈v, w₁〉w₁ + 〈v, w₂〉w₂ + ... + 〈v, wₖ〉wₖ
T adalah transformasi linear mengikuti dari sifat-sifat hasil kali dalam. Misal,
T(u + v) = 〈u + v, w₁〉w₁ + 〈u + v, w₂〉w₂ + ... + 〈u + v, wₖ〉wₖ
= (〈u, w₁〉 + 〈v, w₁〉)w₁ + (〈u, w₂〉 + 〈v, w₂〉)w₂ + ... + (〈u, wₖ〉 + 〈v, wₖ〉)wₖ
= (〈u, w₁〉w₁ + 〈u, w₂〉w₂ + ... + 〈u, wₖ〉wₖ) + (〈v, w₁〉w₁ + 〈v, w₂〉w₂ + ... + 〈v, wₖ〉wₖ)
= T(u) + T(v)
Demikian pula, T(ku) = kT(u).
4. Transformasi Linear dari V ke Rn
Misalkan S = {w₁, w₂, ..., wₙ} adalah basis untuk ruang vektor V berdimensi n, dan misalkan (v)ₛ = (k₁, k₂, ..., kₙ) adalah vektor koordinat relatif terhadap S dari suatu vektor v di V; dengan demikian
v = k₁w₁ + k₂w₂ + ... + kₙwₙ
Definisikan T: V → ℝⁿ sebagai fungsi yang memetakan v ke vektor koordinat relatif terhadap S, yaitu,
T(v) = (v)ₛ = (k₁, k₂, ..., kₙ)
Fungsi T adalah transformasi linear. Untuk melihat bahwa ini benar, misalkan u dan v adalah vektor di V sedemikian sehingga
u = c₁w₁ + c₂w₂ + ... + cₙwₙ dan v = d₁w₁ + d₂w₂ + ... + dₙwₙ
Dengan demikian
(u)ₛ = (c₁, c₂, ..., cₙ) dan (v)ₛ = (d₁, d₂, ..., dₙ)
Tetapi
u + v = (c₁ + d₁)w₁ + (c₂ + d₂)w₂ + ... + (cₙ + dₙ)wₙ
ku = (kc₁)w₁ + (kc₂)w₂ + ... + (kcₙ)wₙ
sehingga
(u + v)ₛ = (c₁ + d₁, c₂ + d₂, ..., cₙ + dₙ)
(ku)ₛ = (kc₁, kc₂, ..., kcₙ)
Oleh karena itu,
(u + v)ₛ = (u)ₛ + (v)ₛ dan (ku)ₛ = k(u)ₛ
Dengan menyatakan persamaan ini dalam bentuk T, kita dapatkan
T(u + v) = T(u) + T(v) dan T(ku) = kT(u)
yang menunjukkan bahwa T adalah transformasi linear.
5. Operator Linear di Pn
Misalkan p = p(x) = c₀ + c₁x + ... + cₙxⁿ adalah suatu polinomial berderajat n, dan misalkan a dan b adalah sembarang skalar. Fungsi T yang didefinisikan oleh
T(p) = T(p(x)) = p(ax + b) = c₀ + c₁(ax + b) + ... + cₙ(ax + b)ⁿ
adalah suatu operator linear.
6. Transformasi Linear menggunakan Hasil Kali Dalam
Misalkan V adalah suatu ruang hasil kali dalam, dan misalkan v₀ adalah suatu vektor tetap di V. Misalkan T: V → ℝ adalah transformasi yang memetakan suatu vektor v ke hasil kali dalam-nya dengan v₀, dengan kata lain,
T(v) = 〈v, v₀〉
Dari sifat-sifat hasil kali dalam,
T(u + v) = 〈u + v, v₀〉 = 〈u, v₀〉 + 〈v, v₀〉 = T(u) + T(v)
dan
T(ku) = 〈ku, v₀〉 = k〈u, v₀〉 = kT(u)
jadi T adalah suatu transformasi linear.
7. Transformasi Linear dari C¹(−∞, ∞) ke F(−∞, ∞)
Misalkan V = C¹(−∞, ∞) adalah ruang vektor dari semua fungsi yang memiliki turunan pertama kontinu pada interval (−∞, ∞), dan misalkan W = F(−∞, ∞) adalah ruang vektor dari semua fungsi bernilai real yang didefinisikan pada interval (−∞, ∞). Misalkan D: V → W adalah transformasi yang memetakan suatu fungsi f = f(x) ke turunan pertamanya, yaitu,
D(f) = f'(x)
Dari sifat-sifat pendiferensialan, kita memiliki
D(f + g) = D(f) + D(g) dan D(kf) = kf'(x) = kD(f)
Dengan demikian, D adalah suatu transformasi linear.
8. Transformasi Linear dari C(−∞, ∞) ke C¹(−∞, ∞)
Misalkan V = C(−∞, ∞) adalah ruang vektor dari semua fungsi kontinu pada interval (−∞, ∞), dan misalkan W = C¹(−∞, ∞) adalah ruang vektor dari semua fungsi yang memiliki turunan pertama kontinu pada interval (−∞, ∞). Misalkan J: V → W adalah transformasi yang memetakan suatu fungsi f = f(x) ke integral
9. Determinan Bukan Transformasi Linear
Misalkan T: Mₙₙ → ℝ adalah transformasi yang memetakan suatu matriks n × n menjadi determinannya:
T(A) = det(A)
Jika n > 1, maka transformasi ini tidak memenuhi salah satu sifat yang diperlukan untuk menjadi transformasi linear. Kita telah mengetahui bahwa
det(A₁ + A₂) ≠ det(A₁) + det(A₂)
secara umum. Selain itu, det(cA) = cⁿ det(A), sehingga
det(cA) ≠ c.det(A)
secara umum. Dengan demikian, T bukan merupakan transformasi linear.
10. Kombinasi Linear dari Transformasi
Jika T: V → W adalah suatu transformasi linear, maka untuk setiap vektor v₁ dan v₂ di V dan setiap skalar c₁ dan c₂, kita memiliki:
T(c₁v₁ + c₂v₂) = T(c₁v₁) + T(c₂v₂) = c₁T(v₁) + c₂T(v₂)
dan, secara lebih umum, jika v₁, v₂, ..., vₙ adalah vektor di V dan c₁, c₂, ..., cₙ adalah skalar, maka:
T(c₁v₁ + c₂v₂ + ... + cₙvₙ) = c₁T(v₁) + c₂T(v₂) + ... + cₙT(vₙ)
Jadi, transformasi linear mempertahankan kombinasi linear.
11. Sifat-Sifat Transformasi Linear
Jika T: V → W adalah suatu transformasi linear, maka:
(a) T(0) = 0
Ini merupakan kasus khusus dari perkalian skalar, yaitu skalar nol pasti menghasilkan vektor nol.
(b) T(−v) = −T(v) untuk semua v di V
Ini merupakan kasus khusus dari perkalian skalar, yaitu ketika skalarnya −1.
(c) T(v − w) = T(v) − T(w) untuk semua v dan w di V
Ini merupakan kasus khusus kombinasi linear.
Poin (a) menyatakan bahwa sebuah transformasi linear memetakan vektor nol (0) ke vektor nol (0). Sifat ini sangat berguna untuk mengidentifikasi transformasi yang bukan linear. Sebagai contoh, jika x₀ adalah vektor taknol yang tetap di R², maka transformasi
T(x) = x + x₀
memiliki efek geometris menggeser setiap titik x pada arah yang sejajar dengan x₀ sejauh ‖x₀‖
Transformasi ini tidak mungkin linear, karena T(0) = x₀, sehingga T tidak memetakan 0 ke 0.
12. Bayangan Vektor Basis
Jika T adalah transformasi matriks, maka matriks standar untuk T dapat diperoleh dari bayangan vektor-vektor basis standar. Dengan kata lain, sebuah transformasi matriks sepenuhnya ditentukan oleh bayangan vektor-vektor basis standarnya. Ini adalah kasus khusus dari hasil yang lebih umum:
Jika T: V → W adalah transformasi linear, dan {v₁, v₂, ..., vₙ} adalah basis untuk V, maka bayangan T(v) dari setiap vektor v di V dapat dihitung dari bayangan
T(v₁), T(v₂), ..., T(vₙ)
dari vektor-vektor basis. Hal ini dapat dilakukan dengan pertama-tama menyatakan v sebagai kombinasi linear dari vektor-vektor basis, yaitu:
v = c₁v₁ + c₂v₂ + ... + cₙvₙ
dan kemudian masukkan ke T
T(v) = c₁T(v₁) + c₂T(v₂) + ... + cₙT(vₙ)
Dengan kata lain, sebuah transformasi linear sepenuhnya ditentukan oleh bayangan dari setiap kumpulan vektor basis.
Contoh:
Perhatikan basis S = {v₁, v₂, v₃} untuk ℝ³, di mana v₁ = (1, 1, 1), v₂ = (1, 1, 0), dan v₃ = (1, 0, 0). Misalkan T: ℝ³ → ℝ² adalah transformasi linear sedemikian sehingga
T(v₁) = (1, 0), T(v₂) = (2, −1), T(v₃) = (4, 3)
Temukan rumus untuk T(x₁, x₂, x₃); kemudian gunakan rumus ini untuk menghitung T(2, −3, 5).
Pertama, kita nyatakan (x₁, x₂, x₃) sebagai kombinasi linear dari v₁ = (1, 1, 1), v₂ = (1, 1, 0), dan v₃ = (1, 0, 0). Jika kita tulis
(x₁, x₂, x₃) = c₁(1, 1, 1) + c₂(1, 1, 0) + c₃(1, 0, 0)
kemudian dengan menyamakan komponen-komponen yang bersesuaian, kita dapatkan
c₁ + c₂ + c₃ = x₁
c₁ + c₂ = x₂
c₁ = x₃
yang menghasilkan c₁ = x₃, c₂ = x₂ − x₃, dan c₃ = x₁ − x₂. Sehingga
(x₁, x₂, x₃) = x₃(1, 1, 1) + (x₂ − x₃)(1, 1, 0) + (x₁ − x₂)(1, 0, 0)
= x₃v₁ + (x₂ − x₃)v₂ + (x₁ − x₂)v₃
Dengan demikian,
T(x₁, x₂, x₃) = x₃T(v₁) + (x₂ − x₃)T(v₂) + (x₁ − x₂)T(v₃)
= x₃(1, 0) + (x₂ − x₃)(2, −1) + (x₁ − x₂)(4, 3)
= (4x₁ − 2x₂ − x₃, 3x₁ − 4x₂ + x₃)
Dari rumus ini, kita dapatkan
T(2, −3, 5) = (9, 23)
13. Komposisi Transformasi Linear
A. Definisi
Jika T₁: U → V dan T₂: V → W adalah transformasi linear, maka komposisi dari T₂ dengan T₁, dinotasikan dengan T₂ ∘ T₁ (yang dibaca "T₂ bundaran T₁"), adalah fungsi yang didefinisikan oleh rumus
(T₂ ∘ T₁)(u) = T₂(T₁(u))
di mana u adalah vektor di U.
Perhatikan bahwa definisi ini mensyaratkan bahwa domain dari T₂ (yaitu V) harus mengandung range dari T₁. Hal ini sangat penting agar rumus T₂(T₁(u)) memiliki arti.
B. Komposisi dari transformasi linear dengan transformasi linear menghasilkan transformasi linear
Jika T₁: U → V dan T₂: V → W adalah transformasi linear, maka T₂ ∘ T₁: U → W juga merupakan transformasi linear.
Jika u dan v adalah vektor di U dan c adalah skalar, maka dari linearitas T₁ dan T₂ diperoleh bahwa
(T₂ ∘ T₁)(u + v) = T₂(T₁(u + v)) = T₂(T₁(u) + T₁(v))
= T₂(T₁(u)) + T₂(T₁(v))
= (T₂ ∘ T₁)(u) + (T₂ ∘ T₁)(v)
dan
(T₂ ∘ T₁)(cu) = T₂(T₁(cu)) = T₂(cT₁(u))
= cT₂(T₁(u)) = c(T₂ ∘ T₁)(u)
Dengan demikian, T₂ ∘ T₁ memenuhi dua syarat untuk menjadi transformasi linear.
C. Perluasan untuk komposisi tiga transformasi linear
Komposisi dapat didefinisikan untuk lebih dari dua transformasi linear. Sebagai contoh, jika
T₁: U → V, T₂: V → W, dan T₃: W → Y
adalah transformasi linear, maka komposisi T₃ ∘ T₂ ∘ T₁ didefinisikan oleh
(T₃ ∘ T₂ ∘ T₁)(u) = T₃(T₂(T₁(u)))
Komposisi ini bisa diperluas untuk lebih dari tiga transformasi linear.


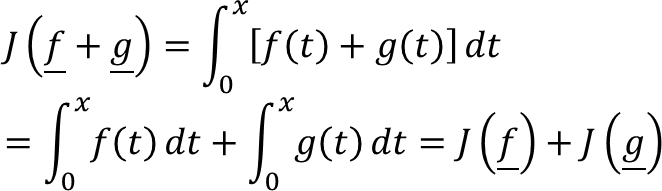




Komentar
Posting Komentar