Persamaan Bidang Singgung Paraboloid Elliptik
1. Bidang Singgung Paraboloid di Titik P(x1, y1, z1) pada Paraboloid yang Puncaknya di O(0, 0, 0)
CALCULUS REQUIRED!
• Suatu paraboloid elliptik umumnya memiliki persamaan:
• Persamaan ini sudah dalam bentuk f(x, y, z) = 0. Gradien garis singgung dapat ditentukan menggunakan turunan parsial pertama, yaitu:
Gradiennya adalah (2x/a², 2y/b², –2p/a²), sederhanakan menjadi (x/a², y/b², –p/a²)
• Misal titik P(x1, y1, z1) terletak pada paraboloid elliptik, gradiennya menjadi (x1/a², y1/b², –p/a²)
• Persamaan bidang melalui P(x1, y1, z1) dengan bilangan arah (x1/a², y1/b², –p/a²):
Bentuk terakhir ini adalah persamaan bidang singgung paraboloid elliptik melalui titik P(x1, y1, z1) yang terletak pada paraboloid elliptik.
2. Bidang Singgung Paraboloid di Titik P(x1, y1, z1) pada Paraboloid yang Puncaknya di M(a, b, g)
Misal suatu paraboloid elliptik puncaknya di O(0, 0, 0), puncaknya digeser ke M(a, b, g), posisi relatifnya akan tergeser, sehingga persamaannya menjadi:
3. Bidang Singgung Paraboloid yang Puncaknya di O(0, 0, 0) dengan Bilangan Arah (A, B, C)
• Misal persamaan paraboloid adalah

• Persamaan bidang singgung melalui titik P(x1, y1, z1) pada paraboloid adalah:
bilangan arahnya (x1/a², y1/b², –p/a²)
• Misal bilangan arah bidang singgung diketahui (A, B, C), diharuskan sebanding dengan (x1/a², y1/b², –p/a²), berlaku perbandingan:
x1/(a²A) = y1/(b²B) = –p/(a²C) = k, dengan k sebagai skala pembanding
kita dapat menuliskan:
x1 = kAa², y1 = kBb²
• Masukkan x1 = kAa², y1 = kBb², p = –kCa² ke persamaan bidang singgung
Bentuk ini adalah persaman bidang singgung paraboloid elliptik dengan bilangan arah (A, B, C)

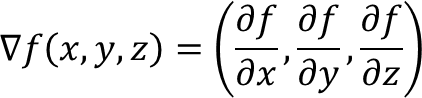





Komentar
Posting Komentar