Fungsi Rasional atau Fungsi Pecah
1. Suku Banyak (Polinomial)
Suku banyak adalah bentuk aljabar yang terdiri dari variabel, konstanta, dan eksponen (pangkat). Bentuk umum suku banyak berderajat n adalah:
P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + aₙ₋₂xⁿ⁻² + ... + a₂x² + a₁x + a₀ dengan aₙ ≠ 0
Keterangan:
n: Derajat suku banyak, sama dengan pangkat tertingginya
a₀, a₁, a₂, ..., aₙ: Koefisien-koefisien suku banyak
Berdasarkan koefisiennya, suku banyak dibagi menjadi:
a. Real Polynomials: Suku banyak dengan koefisien-koefisien yang merupakan bilangan-bilangan real, baik rasional maupun irasional.
b. Rational Polynomials: Suku banyak dengan koefisien-koefisien yang merupakan bilangan-bilangan rasional.
2. Jenis-Jenis Fungsi Rasional (Rational Function) / Fungsi Pecah (Fractional Function)
Fungsi pecah atau rasional adalah suatu fungsi yang dirumuskan sebagai berikut:
f(x) = P(x) / Q(x)
dengan Q(x) ≠ 0, x ∈ R.
dengan P(x) dan Q(x) adalah suku banyak (polinomial).
Berikut ini jenis-jenis fungsi pecah:
A. Fungsi Pecah Rasional (Rational Function)
Fungsi yang berbentuk f(x) = P(x) / Q(x) dengan P(x) dan Q(x) merupakan polinomial dan keduanya tidak memiliki faktor persekutuan.
Contoh:
f(x) = (x² − x − 6)/(x + 5) = (x − 3)(x + 2)/(x + 5)
B. Fungsi Pecah Rasional Tidak Sejati (Improper Rational Function)
Fungsi yang berbentuk f(x) = P(x) / Q(x) dengan P(x) dan Q(x) merupakan polinomial serta derajat P(x) lebih besar atau sama dengan derajat Q(x).
Contoh:
f(x) = x²/(x + 2)
f(x) = (x² − x)/(x² + 5)
f(x) = (x + 1)/(x − 5)
C. Fungsi Pecah Rasional Sejati (Proper Rational Function)
Fungsi yang berbentuk f(x) = P(x) / Q(x) dengan P(x) dan Q(x) merupakan polinomial serta derajat P(x) lebih kecil dari derajat Q(x).
Contoh:
f(x) = x/(x² − 4)
f(x) = (2x − 1)/(x² + 5)
3. Pembuat Nol Fungsi Pecah
Pembuat nol dari suatu fungsi pecah adalah nilai-nilai x yang membuat fungsi tersebut bernilai nol.
Secara matematis, jika kita memiliki fungsi pecah:
f(x) = P(x) / Q(x)
maka pembuat nol dari fungsi f(x) adalah nilai-nilai x yang memenuhi persamaan:
f(x) = 0
Artinya, kita perlu mencari nilai-nilai x yang membuat pembilang P(x) bernilai nol, sementara penyebut Q(x) tidak boleh bernilai nol.
Mengapa demikian?
Jika P(x) = 0 dan Q(x) ≠ 0, maka hasil pembagiannya akan menjadi 0.
Jika Q(x) = 0, maka fungsi tersebut tidak terdefinisi (karena pembagian dengan nol tidak terdefinisi).
Contoh:
Diberikan f(x) = (x² + 3x + 2)/(x + 5)
Pembuat nol pembilang adalah x² + 3x + 2 = 0 ↔ (x + 1)(x + 2) = 0 ↔ x = −1 ∨ x = −2
Pembuat nol penyebut adalah x + 5 = 0 ↔ x = −5
Baik ketika x = −1 maupun x = −2, penyebutnya taknol, sehingga keduanya merupakan pembuat nol.
4. Nilai Kutub Fungsi Pecah
Nilai kutub adalah nilai yang menyebabkan suatu fungsi tidak terdefinisi atau tidak mempunyai nilai.
Jika kita memiliki suatu fungsi yang berbentuk:
f(x) = P(x) / Q(x)
maka nilai yang menyebabkan Q(x) = 0 disebut sebagai nilai kutub dari f(x).
Contoh:
Diberikan f(x) = (x² + 3x + 2)/(x + 5)
Pembuat nol penyebut adalah x + 5 = 0 ↔ x = −5
Jadi, nilai kutubnya adalah −5.
5. Asimtot Fungsi Pecah
Asimtot grafik fungsi f(x) adalah sebuah garis lurus l yang didekati oleh grafik lengkung fungsi f(x) dengan jarak semakin lama semakin kecil mendekati nol di jauh tak terhingga. Dengan kata lain, antara grafik fungsi f(x) dan garis l semakin lama akan semakin berdekatan, tetapi tidak akan memotongnya. Tidak semua grafik fungsi f(x) mempunyai asimtot. Misalnya Grafik fungsi linear dan grafik fungsi kuadrat. Terdapat tiga jenis asimtot pada fungsi rasional pecah, yaitu:
A. Asimtot Tegak
Asimtot tegak terjadi ketika nilai fungsi tidak terdefinisi dan semakin mendekati tak hingga, baik positif maupun negatif.
Untuk menentukannya, cek apakah pembilang dan penyebut memiliki akar persekutuan. Jika ada, sederhanakan terlebih dahulu. Asimtot tegak adalah ketika penyebut bernilai 0 dan pembilang taknol.
Contoh:
Diberikan f(x) = (x² + 3x + 2)/(x² − 1)
difaktorkan menjadi f(x) = (x + 1)(x + 2)/[(x + 1)(x − 1)]
pembilang dan penyebut memiliki akar persekutuan, sehingga disederhanakan menjadi (x + 2)/(x − 1)
Pembuat nol penyebut adalah x − 1 = 0 ↔ x = 1
Asimtot tegaknya adalah x = 1.
B. Asimtot Mendatar
Asimtot mendatar terjadi ketika nilai x semakin mendekati tak hingga, baik positif maupun negatif. Untuk menentukannya dengan melimitkan x menuju tak hingga:
• Derajat P(x) < Q(x), asimtot mendatarnya adalah sumbu x
• Derajat P(x) = Q(x), asimtot mendatarnya adalah hasil bagi koefisien tertinggi
• Derajat P(x) > Q(x), tidak ada asimtot mendatar
Contoh:
Diberikan f(x) = (3x² + x − 2)/(2x² − 5x − 3)
derajat pembilang dan penyebut sama, sehingga asimtot mendatarnya adalah hasil bagi koefisien tertinggi
koefisien tertinggi pembilang adalah 3 dan koefisien tertinggi penyebut adalah 2, sehingga asimtot mendatarnya adalah y = 3/2
C. Asimtot Miring
Asimtot miring adalah asimtot yang tidak sejajar dengan sumbu x maupun sumbu y. Asimtot miring fungsi rasional hanya dimiliki oleh fungsi yang derajat pembilang sama dengan derajat penyebut ditambah satu.
Untuk menentukan asimtot miring, lakukan pembagian pembilang dengan penyebut dan abaikan sisanya, akan diperoleh persamaan asimtot miring.
Contoh:
Diberikan f(x) = (x² + 3x + 2)/(x + 5)
Derajat pembilang adalah 2 dan derajat penyebut adalah 1, ini berarti derajat pembilan sama dengan derajat penyebut ditambah satu, sehingga memiliki asimtot miring.
(x² + 3x + 2)/(x + 5) = x − 2 + 12/(x + 5)
Asimtot miringnya adalah y = x − 2.
Tambahan:
Untuk derajat yang lebih tinggi, akan sulit dilakukan pembagian. Cukup ambil 3 derajat tertinggi untuk pembilang dan ambil 2 derajat tertinggi untuk penyebut, akan diperoleh asimtot miring.
6. Titik Balik Fungsi Pecah
CALCULUS REQUIRED!
Titik balik suatu fungsi adalah ketika garis singgungnya mendatar. Gradien garis singgung dapat ditentukan menggunakan turunan pertama dari suatu fungsi. Garis singgung mendatar ketika gradiennya 0, hal ini terjadi ketika turunan pertama bernilai nol.
Misal f(x) = P(x)/Q(x), turunannya adalah:
f'(x) = [P'(x).Q(x) − P(x).Q'(x)]/[Q(x)]²
Pembilangnya adalah P'(x).Q(x) − P(x).Q'(x) dan penyebutnya adalah [Q(x)]².
Cek apakah memiliki akar persekutuan, jika ada sederhanakan. Bentuk yang sudah disederhanakan, dicari pembuat nol pembilang, sehingga diperoleh titik balik fungsi.
Contoh:
Diberikan f(x) = (x² + 2x + 1)/(x + 2), tentukan titik baliknya.
P(x) = x² + 2x + 1, P'(x) = 2x + 2
Q(x) = x + 2, Q'(x) = 1
Pembilang = P'(x).Q(x) − P(x).Q'(x) = (2x + 2)(x + 2) − (x² + 2x + 1).1 = x² + 4x + 3
pembuat nol pembilang adalah x² + 4x + 3 = 0 ↔ (x + 1)(x + 3) = 0 ↔ x = −1 ∨ x = −3
Penyebut = [Q(x)]² = (x + 2)²
pembuat nol penyebut adalah (x + 2)² = 0 ↔ x = −2
Bentuk sudah sederhana, sehingga kita bisa menentukan titik balik
Untuk x = −1, y = f(x) = ((−1)² + 2(−1) + 1)/(−1 + 2) = 0
Untuk x = −3, y = f(x) = ((−3)² + 2(−3) + 1)/(−3 + 2) = −4
Titik baliknya adalah (−1, 0) dan (−3, −4)
7. Menggambar Grafik Fungsi Pecah
Untuk menggambar grafik fungsi pecah, berikut langkah-langkahnya:
(i) Tentukan titik potong sumbu x dan titik potong sumbu y
(ii) Tentukan asimtot tegak, mendatar, miring (jika ada)
(iii) Buat titik-titik bantu (jika diperlukan)
(iv) Hubungkan titik-titik tersebut menjadi sebuah kurva yang mendekati asimtot tetapi tidak menyentuh
Contoh:
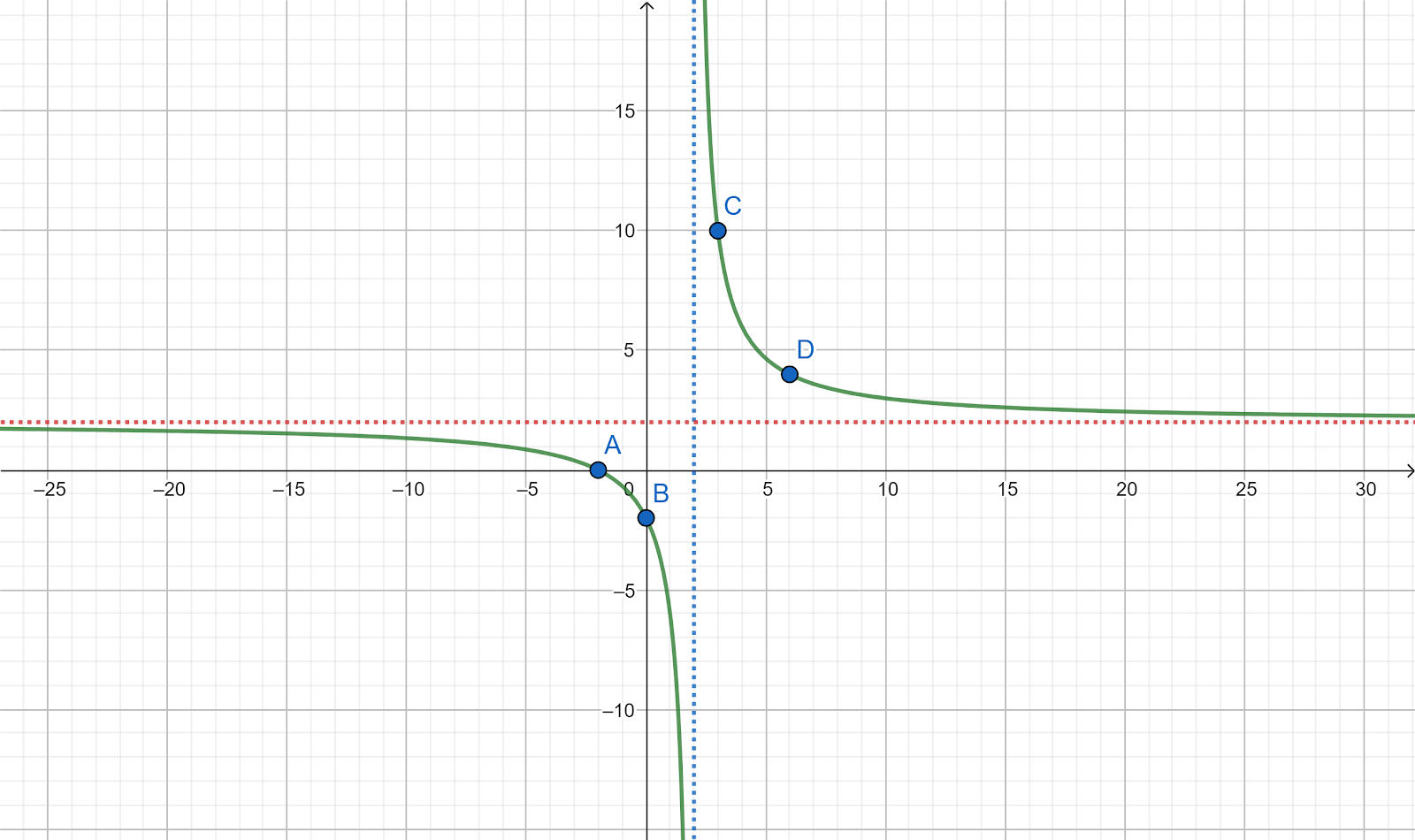
1. Gambarlah grafik fungsi f(x) = (2x + 4)/(x − 2)
• Titik potong sumbu x, yaitu ketika y = f(x) = 0
(2x + 4)/(x − 2) = 0
2x + 4 = 0
x = −2, titik potong sumbu x adalah (−2, 0)
• Titik potong sumbu y, yaitu ketika x = 0
y = f(0) = (2.0 + 4)/(0 − 2) = −2
titik potong sumbu y adalah (0, −2)
• Asimtot tegak, ketika penyebut 0
x − 2 = 0
x = 2
• Asimtot mendatar
Karena pembilang dan penyebut berderajat sama, asimtot mendatarnya adalah hasil bagi koefisien tertinggi, yaitu 2/1 = 2
y = 2
• Titik bantu
x = 3, f(x) = (2.3 + 4)/(3 − 2) = 10, titik (3, 10)
x = 6, f(x) = (2.6 + 4)/(6 − 2) = 4, titik (6, 4)
Berikut grafiknya:
• Titik potong sumbu x, yaitu ketika y = f(x) = 0
(x² − 2x − 3)/(x² − 4) = 0
(x + 1)(x − 3) = 0
x = −1, ∨ x = 3
titik potong sumbu x adalah (−1, 0) dan (3, 0)
• Titik potong sumbu y, yaitu ketika x = 0
y = f(0) = (0² − 2.0 − 3)/(0² − 4) = ¾
titik potong sumbu y adalah (0, ¾)
• Asimtot tegak, ketika penyebut 0
x² − 4 = 0
(x + 2)(x − 2) = 0
x = −2 ∨ x = 2
• Asimtot mendatar
Karena pembilang dan penyebut berderajat sama, asimtot mendatarnya adalah hasil bagi koefisien tertinggi, yaitu 1/1 = 1
y = 1
• Titik bantu
x = −4, y = f(x) = ((−4)² − 2(−4) − 3)/((−4)² − 4) = 7/4, titik (−4, 7/4)
x = −3, y = f(x) = ((−3)² − 2(−3) − 3)/((−3)² − 4) = 12/5, titik (−3, 12/5)
x = 1, y = f(x) = (1² − 2.1 − 3)/(1² − 4) = 4/3, titik (1, 4/3)
x = 4, y = f(x) = (4² − 2.4 − 3)/(4² − 4) = 5/12, titik (4, 5/12)
Berikut grafiknya:



Komentar
Posting Komentar