Identitas Fungsi Siklometri
1. Pengelompokan Fungsi Siklometri menurut Range
Ingat kembali tabel domain dan range fungsi siklometri:
Fungsi | Domain | Range |
x = sin⁻¹(y) | [–1, 1] | [–π/2, π/2] |
x = cos⁻¹(y) | [–1, 1] | [0, π] |
x = tan⁻¹(y) | (–∞, ∞) | (–π/2, π/2) |
x = csc⁻¹(y) | (–∞, –1] ∪ [1, ∞) | [–π/2, 0) ∪ (0, π/2] |
x = sec⁻¹(y) | (–∞, –1] ∪ [1, ∞) | [0, π/2) ∪ (π/2, π] |
x = cot⁻¹(y) | (–∞, ∞) | (0, π) |
Untuk fungsi cos⁻¹, sec⁻¹, dan cot⁻¹, range nya adalah kuadran I dan II, sehingga kita bisa menentukan hubungan antara ketiganya.
Adapun fungsi-fungsi yang berbeda range, kita perlu berhati-hati dalam menentukan hubungannya.
2. Hubungan antara Invers Sinus, Kosekan, dan Tangen
Fungsi-fungsi sin⁻¹, csc⁻¹, dan tan⁻¹, range nya adalah kuadran I dan IV.
Untuk p negatif, sin⁻¹(p), csc⁻¹(p), dan tan⁻¹(p) di kuadran IV, sedangkan untuk p positif, sin⁻¹(p), csc⁻¹(p), dan tan⁻¹(p) di kuadran I.
A. Menentukan Kosekan dan Tangen jika Diketahui Sinus
Misal diberikan sin(θ) = p, kita dapat menentukan csc(θ) dan tan(θ).
B. Menentukan Sinus dan Kosekan jika Diketahui Tangen
Misal diberikan tan(θ) = p, kita dapat menentukan sin(θ) dan csc(θ).
sehingga diperoleh identitas:C. Menentukan Sinus dan Tangen jika Diketahui Kosekan
Misal diberikan csc(θ) = p, kita dapat menentukan sin(θ) dan tan(θ).
Fungsi-fungsi cos⁻¹, sec⁻¹, dan cot⁻¹, range nya adalah kuadran I dan II.
Untuk p negatif, cos⁻¹(p), sec⁻¹(p), dan cot⁻¹(p) di kuadran II, sedangkan untuk p positif, cos⁻¹(p), sec⁻¹(p), dan cot⁻¹(p) di kuadran I.
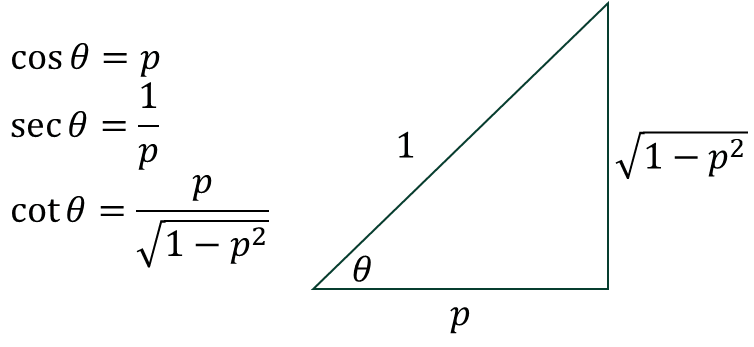
A. Menentukan Sekan dan Kotangen jika Diketahui Kosinus
Misal diberikan cos(θ) = p, kita dapat menentukan sec(θ) dan cot(θ).
sehingga diperoleh identitas:
B. Menentukan Kosinus dan Kotangen jika Diketahui Sekan
Misal diberikan sec(θ) = p, kita dapat menentukan cos(θ) dan cot(θ).
sehingga diperoleh identitas:C. Menentukan Kosinus dan Sekan jika Diketahui Kotangen
Misal diberikan cot(θ) = p, kita dapat menentukan cos(θ) dan sec(θ).
A. Resiprokal dengan Range Sama
Ingat kembali:
sin(x) = 1/csc(x)
csc(x) = 1/sin(x)
cos(x) = 1/sec(x)
sec(x) = 1/cos(x)
Sehingga berlaku:
sin⁻¹(1/p) = csc⁻¹(p)
csc⁻¹(1/p) = sin⁻¹(p)
cos⁻¹(1/p) = sec⁻¹(p)
sec⁻¹(1/p) = cos⁻¹(p)
B. Resiprokal dengan Range Beda
Ingat kembali:
tan(x) = 1/cot(x)
cot(x) = 1/tan(x)
Akan tetapi perlu diketahui bahwa range dari tan⁻¹(x) adalah (–π/2, π/2) dan range dari cot⁻¹(x) adalah (0, π), sehingga diperlukan kehati-hatian dalam identitas resiprokal.
Ingat juga sudut yang berelasi:
tan(π + x) = tan(x), dan cot(π + x) = cot(x)
Rumus ini bisa kita gunakan untuk menyesuaikan range, sehingga:
tan⁻¹(1/p) = cot⁻¹(p), untuk p positif
tan⁻¹(1/p) = cot⁻¹(p) – π, untuk p negatif
cot⁻¹(1/p) = tan⁻¹(p), untuk p positif
cot⁻¹(1/p) = tan⁻¹(p) + π, untuk p negatif
4. Identitas Berlawanan Tanda
Ingat kembali sudut yang berelasi:
sin(–x) = –sin(x)
tan(–x) = –tan(x)
csc(–x) = –csc(x)
cos(π – x) = –cos(x)
sec(π – x) = –sec(x)
cot(π – x) = –cot(x)
Sehingga berlaku:
sin⁻¹(p) + sin⁻¹(–p) = 0
tan⁻¹(p) + tan⁻¹(–p) = 0
csc⁻¹(p) + csc⁻¹(–p) = 0
cos⁻¹(p) + cos⁻¹(–p) = π
sec⁻¹(p) + sec⁻¹(–p) = π
cot⁻¹(p) + cot⁻¹(–p) = π
5. Identitas Komplementer
Ingat kembali sudut yang berelasi:
sin(π/2 – α) = cos(α), csc(π/2 – α) = sec(α)
cos(π/2 – α) = sin(α), sec(π/2 – α) = csc(α)
tan(π/2 – α) = cot(α), cot(π/2 – α) = tan(α)
Sehingga berlaku:
sin⁻¹(p) + cos⁻¹(p) = π/2
sec⁻¹(p) + csc⁻¹(p) = π/2
tan⁻¹(p) + cot⁻¹(p) = π/2
6. Hubungan Antar Fungsi di Kuadran I
Semua fungsi siklometri memiliki range di kuadran I, dimana semua perbandingan trigonometri bernilai positif. Berikut tabel yang berlaku hanya di kuadran I:
Untuk p positif, range fungsi-fungsi siklometri adalah kuadran I, sehingga bisa diperoleh hubungan antar fungsi-fungsi siklometri.
7. Jumlah dan Selisih Fungsi Siklometri di Kuadran I
A. Jumlah dan Selisih Invers Sinus
Diberikan p dan q dengan 0 < p < 1 dan 0 < q < 1. Misal sin⁻¹(p) = α dan sin⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Selisih invers sinus
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers sinus range nya adalah range invers sinus
sin⁻¹(p) – sin⁻¹(q) = α – β, ingat kembali rumus sinus selisih sudut
sin(α – β) = sin(α).cos(β) – cos(α).sin(β)
0 < α + β < π, sehingga untuk jumlah invers sinus range nya adalah range invers kosinus
sin⁻¹(p) + sin⁻¹(q) = α + β, ingat kembali rumus kosinus jumlah sudut
cos(α + β) = cos(α).cos(β) – sin(α).sin(β)
B. Jumlah dan Selisih Invers Kosinus
Diberikan p dan q dengan 0 < p < 1 dan 0 < q < 1. Misal cos⁻¹(p) = α dan cos⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Jumlah invers kosinus
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
0 < α + β < π, sehingga untuk jumlah invers kosinus range nya adalah range invers kosinus
cos⁻¹(p) + cos⁻¹(q) = α + β, ingat kembali rumus kosinus jumlah sudut
cos(α + β) = cos(α).cos(β) – sin(α).sin(β)
• Selisih invers kosinus
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers kosinus range nya adalah range invers sinus
cos⁻¹(p) – cos⁻¹(q) = α – β, ingat kembali rumus sinus selisih sudut
sin(α – β) = sin(α).cos(β) – cos(α).sin(β)
AIO jumlah dan selisih invers sinus dan kosinus:Diberikan p dan q dengan p > 0 dan q > 0. Misal tan⁻¹(p) = α dan tan⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Selisih invers tangen
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers tangen range nya adalah range invers tangen
tan⁻¹(p) – tan⁻¹(q) = α – β, ingat kembali rumus tangen selisih sudut
• Jumlah invers tangen
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
0 < α + β < π, sehingga untuk jumlah invers tangen range nya adalah range invers kotangen
tan⁻¹(p) + tan⁻¹(q) = α + β, ingat kembali rumus kotangen jumlah sudut
D. Jumlah dan Selisih Invers Kotangen
Diberikan p dan q dengan p > 0 dan q > 0. Misal cot⁻¹(p) = α dan cot⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Jumlah invers kotangen
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
0 < α + β < π, sehingga untuk jumlah invers kotangen range nya adalah range invers kotangen
cot⁻¹(p) + cot⁻¹(q) = α + β, ingat kembali rumus kotangen jumlah sudut
• Selisih invers kotangen
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers kotangen range nya adalah range invers tangen
cot⁻¹(p) – cot⁻¹(q) = α – β, ingat kembali rumus tangen selisih sudut
AIO jumlah dan selisih invers tangen dan kotangen:E. Jumlah dan Selisih Invers Sekan
Diberikan p dan q dengan p > 1 dan q > 1. Misal sec⁻¹(p) = α dan sec⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Jumlah invers sekan
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
0 < α + β < π, sehingga untuk jumlah invers sekan range nya adalah range invers sekan
sec⁻¹(p) + sec⁻¹(q) = α + β, ingat kembali rumus sekan jumlah sudut
• Selisih invers sekan
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers sekan range nya adalah range invers kosekan
sec⁻¹(p) – sec⁻¹(q) = α – β, ingat kembali rumus kosekan selisih sudut
F. Jumlah dan Selisih Invers Kosekan
Diberikan p dan q dengan p > 1 dan q > 1. Misal csc⁻¹(p) = α dan csc⁻¹(q) = β, interval untuk α dan β adalah 0 < α < π/2 dan 0 < β < π/2.
• Selisih invers kosekan
Selisih α – β ada pada interval 0 – π/2 < α – β < π/2 – 0
– π/2 < α – β < π/2, sehingga untuk selisih invers kosekan range nya adalah range invers kosekan
csc⁻¹(p) – csc⁻¹(q) = α – β, ingat kembali rumus kosekan selisih sudut
• Jumlah invers kosekan
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
Jumlah α + β ada pada interval 0 + 0 < α + β < π/2 + π/2
0 < α + β < π, sehingga untuk jumlah invers kosekan range nya adalah range invers sekan
csc⁻¹(p) + csc⁻¹(q) = α + β, ingat kembali rumus sekan jumlah sudut
AIO jumlah dan selisih invers sekan dan kosekan:Contoh Soal
1. Tentukan domain dan range dari fungsi
θ = 3.sin⁻¹(x/4 + 1)
domain:
–1 ≤ x/4 + 1 ≤ 1
–2 ≤ x/4 ≤ 0
–8 ≤ x ≤ 0
domainnya adalah [–8, 0]
range:
3.(–π/2) ≤ θ ≤ 3.(π/2)
–3π/2 ≤ θ ≤ 3π/2
rangenya adalah [–3π/2, 3π/2]
Jadi, domainnya adalah [–8, 0] dan rangenya adalah [–3π/2, 3π/2]
2. Hitunglah cot⁻¹(3) + sin⁻¹(1/√5)
Misal cot⁻¹(3) = α ↔ cot(α) = 3, karena cot(α) positif, kita bisa menentukan sin(α)
sin(α) = 1/√10 → cos(α) = 3/√10
sin(β) = 1/√5 → cos(β) = 2/√5
cos(α + β) = cos(α).cos(β) – sin(α).sin(β)
= (3/√10).(2/√5) – (1/√10).(1/√5)
= 5/√50
= 1/√2
α + β = cos⁻¹(1/√2) = π/4
3. Hitunglah tan⁻¹(3) + 2.tan⁻¹(½) + 3.tan⁻¹(⅓)
tan⁻¹(3) + 2.tan⁻¹(½) + 3.tan⁻¹(⅓) = tan⁻¹(3) + tan⁻¹(⅓) + 2.tan⁻¹(½) + 2.tan⁻¹(⅓)
= tan⁻¹(3) + tan⁻¹(⅓) + 2[tan⁻¹(½) + tan⁻¹(⅓)]
4. Buktikan bahwa
= cos⁻¹(2.cos²(α) – 1)
= cos⁻¹(1 + x – 1)
= cos⁻¹(x) ∎






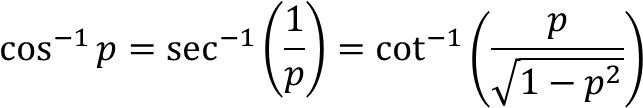







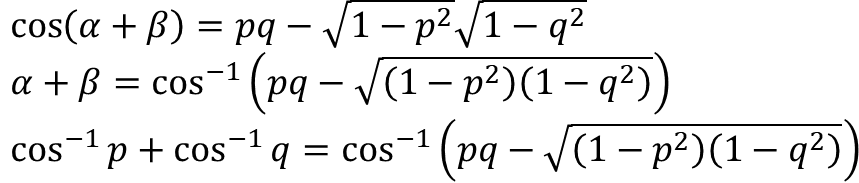
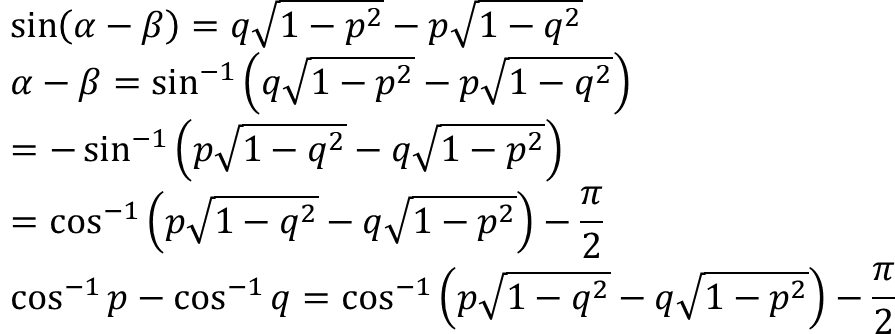












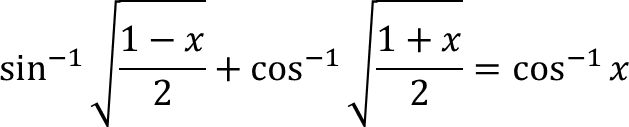




Komentar
Posting Komentar