Peluang (Teopro)
1. Peluang
Definisi: Misalkan 𝐴 adalah kejadian yang bersesuaian dengan suatu eksperimentasi untuk ruang sampel 𝑆 yang berhingga dengan setiap titik sampel berkemungkinan sama untuk terjadi. Peluang kejadian 𝐴, yaitu 𝑃(𝐴), didefinisikan sebagai:
contoh:
Sebuah dadu yang bernomorkan 1 - 6 di lempar, tentukan peluang munculnya matadadu genap!
A = {2, 4, 6}, n(A) = 3
S = {1, 2, 3, 4, 5, 6}, n(S) = 6
P(A) = n(A) / n(S) = 3 / 6 = ½
2. Gabungan dan Irisan Kejadian
Gabungan dua kejadian A dan B, dinyatakan dengan 𝐴 ∪ 𝐵, merupakan kejadian yang mengandung semua elemen yang termasuk A atau B atau keduanya.
Irisan dua kejadian A dan B, dinyatakan dengan 𝐴 ∩ 𝐵, merupakan kejadian yang elemennya termasuk dalam A dan B.
Jika 𝐴 dan 𝐵 adalah kejadian-kejadian dalam ruang sampel 𝑆, maka
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
3. Kejadian Saling Asing / Saling Lepas
Definisi: Kejadian A dan B di dalam ruang sampel S disebut kejadian yang saling asing (disjoint) jika dan hanya jika A ∩ B = ∅.
Dengan kata lain, kejadian yang saling asing adalah kejadian yang tidak mungkin terjadi bersamaan.
Berdasarkan definisi, peluang gabungan kejadian yang saling asing adalah:
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
= 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(∅)
= 𝑃(𝐴) + 𝑃(𝐵) − 0
= 𝑃(𝐴) + 𝑃(𝐵)
Jadi, peluang gabungan kejadian yang saling asing adalah 𝑃(𝐴) + 𝑃(𝐵).
4. Kejadian Saling Bebas
Definisi: Jika A dan B kejadian saling bebas, maka 𝑃(𝐴 | 𝐵) = 𝑃(𝐴) karena terjadinya kejadian A tidak dipengaruhi oleh kejadian B. Akibatnya kejadian A dan B saling bebas jika dan hanya jika
P(A ∩ B) = P(A).P(B)
contoh:
Di dalam sebuah kotak terdapat 4 bola merah, 3 bola putih, dan 1 bola hitam. Sebuah bola diambil secara acak lalu dikembalikan ke kotak, peluang terambilnya bola merah pada pengambilan pertama dan bola putih pada pengambilan kedua adalah:
P(A ∩ B) = P(A).P(B) = ½ × ⅜ = 3/16
5. Kejadian bersyarat
Kejadian B dengan syarat kejadian A adalah terjadinya kejadian B jika kejadian A telah terjadi, dinotasikan dengan B | A.
Jika A dan B dua kejadian dalam ruang sampel S dengan P(A) ≠ 0, maka peluang kejadian B jika diketahui kejadian A didefinisikan sebagai :
yang mana ekivalen dengan:
𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴) × 𝑃(𝐵 | 𝐴)
contoh:Misalkan dalam sebuah kotak terdapat 6 bola kuning dan 4 bola hitam. Dua bola akan diambil berturut-turut tanpa dikembalikan. Tentukan peluang diperolehnya bola hitam pada pengambilan pertama dan bola kuning pada pengambilan kedua!
Peluang diperolehnya bola hitam pada pengambilan pertama = 4/10 = ⅖
Setelah terambil bola hitam pada pengambilan pertama, dan tidak dikembalikan lagi, banyak bola dalam kotak tersisa 9, sehingga n(S) = 9, sehingga:
Peluang diperolehnya bola kuning pada pengambilan kedua = 6/9 = ⅔
Sehingga
𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴) × 𝑃(𝐵 | 𝐴) = ⅖ × ⅔ = 4/15
Contoh Soal
1. Iwan dan Doni mengikuti ujian penerimaan PNS. Peluang Iwan diterima PNS adalah 1/4, sedangkan peluang Doni diterima PNS adalah adalah 2/5. Jika hasil ujian iwan dan Doni tidak saling mempengaruhi (saling bebas), maka tentukan peluang bahwa “Iwan tidak diterima tetapi Doni diterima PNS”!
Misal kejadian D = Doni diterima PNS, I = Iwan diterima PNS
P(D) = 2/5, P(I) = 1/4
Karena saling bebas, P(D ∩ I) = P(D) × P(I) = 2/5 × 1/4 = 1/10
P(D ∩ IC) = P(D) − P(D ∩ I) = 2/5 − 1/10 = 3/10.
Jadi, peluang bahwa Iwan tidak diterima tetapi Doni diterima PNS adalah 3/10.
2. Setelah lulus dari SMA peluang Andi kuliah adalah 0,6 dan peluang Andi bekerja adalah 0,5. Sementara itu jika ternyata Andi tidak kuliah peluang Andi bekerja 0,7. Jika Andi tidak bekerja, tentukan peluang Andi kuliah!
Misal kejadian K = Andi kuliah, B = Andi bekerja
P(K) = 6/10, P(KC) = 1 − P(K) = 1 − 6/10 = 4/10
P(B) = 5/10, P(BC) = 1 − P(B) = 1 − 5/10 = 5/10
P(B | KC) = 7/10
P(B ∩ KC) = P(KC) × P(B | KC) = 4/10 × 7/10 = 28/100
P(B ∩ K) = P(B) − P(B ∩ KC) = 5/10 − 28/100 = 22/100
P(K ∩ BC) = P(K) − P(K ∩ B) = 6/10 − 22/100 = 38/100
P(K | BC) = (K ∩ BC) / P(BC) = (38/100) / (5/10) = 76/100 = 0,76
Jadi, jika Andi tidak bekerja, peluang Andi kuliah adalah 0,76.
3. Diberikan P(A) = 1/2, P(B) = 1/3, dan P(A ∩ B) = 1/4, tentukan P(AC | BC)!
P(A) = 1/2, P(AC) = 1 − P(A) = 1/2
P(B) = 1/3, P(BC) = 1 − P(B) = 2/3
P(A ∩ B) = 1/4
P(A ∩ BC) = P(A) − P(A ∩ B) = 1/2 − 1/4 = 1/4
P(AC ∩ BC) = P(BC) − P(A ∩ BC) = 2/3 − 1/4 = 5/12
P(AC | BC) = P(AC ∩ BC) / P(BC) = (5/12) / (2/3) = 5/8
4. Dua buah dadu dilempar secara bersama sebanyak 1 kali. Berapa probabilitas kejadian munculnya angka 1 untuk dadu kedua dengan syarat kejadian munculnya jumlah kedua dadu kurang dari 4 terjadi lebih dahulu ?
Misal kejadian A = Munculnya angka 1 untuk dadu kedua, B = Jumlah kedua dadu kurang dari 4
n(S) = 6 × 6 = 36
A = {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1)}
B = {(1, 1), (1, 2), (2, 1)}, n(B) = 3
P(B) = n(B) / n(S) = 3/36 = 1/12
A ∩ B = {(1, 1), (2, 1)}, n(A ∩ B) = 2
P(A ∩ B) = n(A ∩ B)/n(S) = 2/36 = 1/18
P(A | B) = P(A ∩ B)/P(B) = (1/18) / (1/12) = 2/3
Jadi, peluang munculnya angka 1 untuk dadu kedua dengan syarat munculnya jumlah kedua dadu kurang dari 4 adalah 2/3.
5. Sebuah dompet berisi uang logam, 5 keping lima ratusan dan 2 keping seratusan rupiah. Dompet yang lain berisi uang logam 1 keping lima ratusan dan 3 keping seratusan rupiah. Jika sebuah uang logam diambil secara acak dari salah satu dompet, tentukan probabilitas untuk mendapatkan uang logam seratusan rupiah.
Misal kejadian A = Terambil dari dompet 1, AC = Terambil dari dompet 2
B = Terambil uang logam seratusan rupiah, BC = Terambil uang logam lima ratusan
Karena tidak diberikan peluang terambil dari masing-masing dompet secara khusus, anggap saja peluang terambil dari masing-masing dompet adalah sama, yaitu 1/2.
P(A) = 1/2, P(AC) = 1/2
P(B | A) = n(B ∩ A)/n(A) = 2/(5 + 2) = 2/7
P(B ∩ A) = P(B | A) × P(A) = 2/7 × 1/2 = 1/7
P(B | AC) = n(B ∩ AC)/n(AC) = 3/(1 + 3) = 3/4
P(B ∩ AC) = P(B | AC) × P(AC) = 3/4 × 1/2 = 3/8
P(B) = P(B ∩ A) + P(B ∩ AC) = 1/7 + 3/8 = 29/56
6. Diberikan A dan B dua kejadian yang saling bebas, tetapi tidak saling lepas dengan P(A) = 1/3 dan P(A ∪ B) = 3/5. Tentukan P(B)!
P(A) = 1/3, P(A ∪ B) = 3/5
P(A ∩ B) = P(A) + P(B) − P(A ∪ B) = 1/3 + P(B) − 3/5 = P(B) − 4/15
Karena saling bebas, P(A ∩ B) = P(A).P(B), sehingga
(1/3).P(B) = P(B) − 4/15
(2/3).P(B) = 4/15
P(B) = (4/15) × (3/2) = 2/5



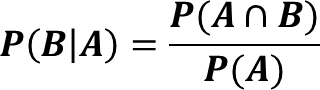


Komentar
Posting Komentar