Analisis Regresi Linear Sederhana
Pengujian Inferensial yang sering digunakan:
➢ Pengujian Komparasi (Dua Sampel → Uji t, Tiga Sampel atau lebih → Analisis Variansi)
➢ Pengujian Asosiasi, yaitu Menguji apakah terdapat hubungan (relasi) antara dua atau lebih variabel
Suatu hubungan dapat dinyatakan dalam suatu rumusan model matematika, yang dengan rumusan tersebut dapat dilakukan suatu prediksi → Analisis Regresi (Regression)
Reliabilitas dari prediksi akan bergantung pada kekuatan relasi antara variabel-variabel yang terikat oleh rumusan → Analisis Korelasi (Correlation)
Regresi vs Korelasi
▪ Regresi digunakan untuk melakukan prediksi melalui model statistika (formula matematika) nilai variabel terikat berdasar nilai variabel bebas, sedangkan korelasi digunakan untuk menentukan kekuatan hubungan (the strength of association) antara variabel-variabel bebas dan variabel terikat.
▪ Setiap regresi pasti korelasi, tetapi belum tentu setiap korelasi merupakan regresi.
▪ Regresi tidak berlaku hubungan bolak-balik, sedangkan korelasi berlaku hubungan bolak-balik.
Analisis regresi merupakan suatu studi yang mempelajari ketergantungan satu variabel (variabel yang diterangkan / the explained variable) dengan satu atau dua variabel yang menerangkan (the explanatory variable).
Variabel pertama disebut variabel dependen / terikat / respon dan variabel kedua kedua disebut variabel independen / bebas / prediktor. Analisis regresi merupakan pengujian statistika inferensial yang bertujuan untuk predikasi atau peramalan yang didasarkan pada model statistik (dalam bentuk rumusan matematika) nilai-nilai variabel terikat Y (variabel respon) berdasarkan nilai-nilai variabel bebas X (variabel prediktor) dengan variabel-variabelnya berskala interval.
Secara sederhana, regresi linear sederhana merupakan analisis regresi yang hanya melibatkan satu variabel terikat dan satu variabel bebas. Dalam analisis regresi linear sederhana, dikonstruksi model linear untuk memprediksi nilai variabel terikat berdasarkan nilai dari satu variabel bebas.
➤ Misalkan terdapat n pasangan observasi yang independen yaitu (X₁,Y₁), (X₂,Y₂), ..., (Xₙ, Yₙ) dengan Xᵢ adalah nilai ke-i dari variabel bebas dan Yᵢ adalah nilai ke-i dari variabel terikat. Pasangan-pasangan observasi tersebut digunakan untuk membangun model linear yang dapat digambarkan dalam diagram pencar pada bidang kartesius dimana setiap pasangan dapat dinyatakan dengan sebuah titik.
1. Model Regresi Linear Sederhana
Persamaan regresi linear sederhana merupakan persamaan matematika yang memungkinkan peramalan nilai suatu variabel terikat dari suatu nilai variabel bebas. Model hubungan linear sederhana variabel terikat Y atas variabel bebas X pada populasi:
Yᵢ = α + βXᵢ + εᵢ
Keterangan
Yᵢ: nilai ke-i variabel Y
𝛼: konstanta atau suku tetap (rerata populasi jika X = 0)
𝛽: koefisien regresi Y atas X
εᵢ: galat random dari Y pada pengamatan ke-i yang berdistribusi normal dengan rerata 0 dan variansi 𝜎²
Efek perubahan variabel bebas pada variable terikat → setiap perubahan satu unit pada variable bebas diharapkan akan terjadi perubahan 𝛽 unit pada variable terikat.
2. Data Sampel
Pada pengujian statistika inferensial yang melibatkan sampel, tidak dapat ditentukan nilai α dan β sehingga perlu digunakan estimator-estimator untuk α, β, dan ε. Misal a adalah estimator untuk α, b estimator untuk β, dan e estimator untuk ε, maka model regresi linear sederhana antara X dan Y pada sampel:
Yᵢ = a + bXᵢ + eᵢ
Garis regresi merupakan suatu garis yang digunakan untuk memprediksi nilai Y jika nilai X diketahui. Adapun persamaan garis regresi linear sederhana adalah sebagai berikut.
Ŷ = a + bX
dengan Ŷ (Y topi) merupakan nilai Y prediktif jika nilai X diketahui yang memungkinkan tidak sama dengan nilai Y sesungguhnya pada data, a disebut intercept, dan b disebut slope. Selisih antara nilai Y sesungguhnya dengan nilai Ŷ prediktif yang disebut dengan galat atau residu yaitu eᵢ = Yᵢ − Ŷᵢ.
Garis regresi harus berada di sekitar titik (Xᵢ, Yᵢ) dan umumnya hanya dapat menarik garis lurus disekitar titik (Xᵢ, Yᵢ) → tidak semua titik dilalui oleh garis. Konsekuensinya kita harus mencari garis yang paling dekat dengan semua titik-titik (Xᵢ, Yᵢ).
Garis regresi akan dekat dengan titik-titik (Xᵢ, Yᵢ) jika jumlah kuadrat residu paling kecil. Akibatnya metode pencarian persamaan garis regresi dicari (menentukan nilai a dan b) dengan menggunakan metode kuadrat terkecil (least squares method).
3. Metode Kuadrat Terkecil (Least Squares Method)
Persamaan garis regresi linear sederhana (mencari nilai 𝑎 dan 𝑏) dilakukan dengan dengan meminimalkan nilai dari
Perhatikan bahwa jika nilai 𝐷 = 0 yaitu selisih antara nilai data yang akan didekati dengan hasil pemodelan mendekati 0, maka menunjukkan bahwa hasil pemodelan akan berhimpit dengan data sesunguhnya.
Mendapatkan varians sisa yang mendekati 0 adalah dengan mendapatkan nilai kritis 𝑎 dan 𝑏 sehingga nilai 𝐷 minimum.
Turunkan D terhadap a secara parsial, untuk meminimumkan D, diharuskan turunannya 0
Turunkan D terhadap b secara parsial, untuk meminimumkan D, diharuskan turunannya 0
Masukkan (i) ke (ii)
Masukkan (i) ke (ii)
Cara lain untuk menentukan a dan b
Contoh:
Penelitian untuk mengetahui ada tidaknya hubungan antara variabel frekuensi penyiraman per pekan (x) dan kecepatan pertumbuhan tanaman (y) pada 10 kali eksperimen.
Buat tabel bantu:
|
Freq (X) |
Kec (Y) |
XY |
X2 |
Y2 |
|
8 |
2,8 |
22,4 |
64 |
7,84 |
|
9 |
3,1 |
27,9 |
81 |
9,61 |
|
7 |
2,5 |
17,5 |
49 |
6,25 |
|
6 |
2,2 |
13,2 |
36 |
4,84 |
|
7 |
2,3 |
16,1 |
49 |
5,29 |
|
8 |
2,7 |
21,6 |
64 |
7,29 |
|
9 |
2,9 |
26,1 |
81 |
8,41 |
|
6 |
2,1 |
12,6 |
36 |
4,41 |
|
5 |
1,9 |
9,5 |
25 |
3,61 |
|
5 |
1,6 |
8 |
25 |
2,56 |
|
70 |
24,1 |
174,9 |
510 |
60,11 |
Sehingga persamaan regresi kecepatan pertumbuhan tanaman pada frekuensi penyiraman per pekan adalah:
Ŷ = 0,24 + 0,31X
Persamaan regresi tersebut menunjukkan bahwa setiap perubahan satu unit pada frekuensi penyiraman, diperkirakan akan terjadi perubahan sebesar 0,31 pada kecepatan pertumbuhan.
4. Prediksi
Dengan menggunakan persamaan regresi Ŷ = 0,24 + 0,31X, dapat dilakukan prediksi terhadap kecepatan pertumbuhan tanaman (variabel Y) menurut frekuensi penyiraman per pekan (variabel X), misal pada suatu eksperimen dilakukan 10 kali penyiraman per pekan, maka kecepatan pertumbuhan diprediksi:
Ŷ = 0,24 + (0,31)(10) = 3,34
Ini berarti jika dilakukan 10 kali penyiraman per pekan, maka kecepatan pertumbuhan diprediksi 3,34 (prediksi ini tidak sepenuhnya benar, namun peluangnya sangat tinggi).
➤ Perlu dipahami bahwa pada prediksi yang dimaksud adalah interpolasi, bukan ekstrapolasi → kita melakukan prediksi hanya untuk nilai-nilai X yang berada pada domainnya (di luar domain tidak diperbolehkan melakukan prediksi karena memungkinkan model tidak linear lagi).
Misal domain untuk X dibatasi pada 3 sampai 15 kali penyiraman per pekan, maka model ini tidak bisa digunakan untuk memprediksi penyiraman 16 kali per pekan, karena diluar domain.
5. Variasi Regresi Linear
Untuk suatu nilai Xᵢ variasi nilai pengamatan Y disebabkan oleh (Sumber Variasi):
➤ Menyimpangnya nilai amatan Yᵢ terhadap dugaan nilai harapan Ŷᵢ = a + bXᵢ
Yᵢ − Ŷᵢ = eᵢ → karena galat / sesatan / sisaan
➤ a dan b bervariasi sehingga menghasilkan dugaan garis regresi yang bervariasi
Menyimpangnya suatu dugaan garis regresi terhadap rerata sehingga menyebabkan bervariasinya data
Ŷᵢ − Ȳ = a + bXᵢ − Ȳ → karena model regresi
Variasi pada regresi linear digunakan untuk mengetahui seberapa baik variabel bebas dapat
memprediksi variabel terikat.
➢ Variasi Total (Total Variation)
Ukuran variasi nilai-nilai 𝑌 (Variable Terikat) amatan disekitar nilai reratanya, tanpa memperhatikan sama sekali nilai-nilaia 𝑋 (Variable Bebas)
Rumus Variasi Total (Jumlah Kuadrat Total)
Dengan melibatkan skor mentah diperoleh
Variasi total dapat didekomposisi menjadi dua yaitu:
1) Variasi yang dapat dijelaskan (Explained Variation), berkontribusi terhadap model yang berkaitan dengan X dan Y → Jumlah Kuadrat karena Regresi (Sum of Squares due to Regression)
2) Variasi yang tidak dapat dijelaskan (Unexplained Variation), tidak berkontribusi terhadap model → Jumlah Kuadrat Galat (Error Sum of Squares)
Ini berarti berlaku hubungan:
JKT = JKR + JKG
➢ Explained Variation
Variasi yang dapat dijelaskan disebut Jumlah Kuadrat karena Regresi (JKR) yang menunjukkan dirumuskan:
Dengan melibatkan skor mentah diperoleh:
➢ Unexplained Variation
Variasi yang tidak dapat dijelaskan disebut Jumlah Kuadrat Galat (JKG) yang menunjukkan dirumuskan:
Menyimpangnya nilaia amatan Y terhadap dugaan nilai harapan Ŷ dikarenakan eror/galat
Dengan melibatkan skor mentah diperoleh:Koefisien determinasi merupakan persentase atau proporsi varians Y (variabel terikat) yang dapat dijelaskan oleh X (variabel bebas) melalui model hubungan yang diperoleh.
Koefisein determinasi regresi linear antara X dan Y dinyatakan sebagai berikut.
r² = JKR/JKT = 1 − JKG/JKT
Dapat dilihat bahwa Koefisien Determinasi bagian dari Varians Total yang dijelaskan oleh model hubungan linear sederhana.
Perhatikan JKT = JKR + JKG sehingga nilai JKT akan lebih besar daripada JKG, sehingga nilai pembagian JKG dan JKT akan berada pada rentang antara 0 dan 1. Akibatnya bahwa
0 ≤ r² ≤ 1
Berdasarkan pada contoh penerapan sebelumnya diperoleh persamaan garis regresi kecepatan pertumbuhan pada frekuensi penyiraman.
Ŷ = 0,24 + 0,31X
Akibatnya nilai varians pada regresi tersebut:
r² = JKR/JKT = (1,922)/(2,029) = 0,947265
Ini berarti bahwa 94,7% nilai-nilai Y (kecepatan pertumbuhan) dapat dijelaskan oleh model regresi linearnya berdasarkan nilai-nilai X (frekuensi penyiraman). Atau dengan kata lain sebesar 94,7% variasi pada kecepatan pertumbuhan terjelaskan oleh frekuensi penyiraman melalui regresi linear
Ŷ = 0,24 + 0,31X
7. Kesalahan Baku Taksiran dan Koefisien Regresi
Metode kuadrat terkecil menyatakan bahwa garis yang diperoleh merupakan garis dengan jarak vertikal antara Y amatan dan Y prediktif (Ŷ) di atas garis dan di bawah garis seimbang sedemikian sehingga Σ(Y – Ŷ) = 0 untuk setiap Y.
Kesalahan Baku/Selisih Taksir Standar yaitu indeks yang digunakan untuk mengukur tingkat ketepatan regresi (pendugaan) dan koefisien regresi (penduga) atau mengukur variasi titik-titik di sekitar garis regresi. Sehingga terdapat batasan seberapa jauh melesatnya perkiraan dalam memprediksikan data dapat diketahui.
Jika semua data amatan terletak pada garis regresi, maka kesalahan baku akan sama dengan nol. Dengan kata lain prediksi yang dilakukan terhadap data sesuai dengan data sebenarnya.
Kesalahan baku taksiran (Standard Error Estimate) yaitu untuk mengukur tingkat variabilitas nilai-nilai Y di sekitar garis regresi ditentukan dengan kesalahan baku taksiran, yaitu sy.x atau sy|x dirumuskan dengan:
Semakin tinggi kesalahan baku estimasi maka semakin lemah persamaan regresi tersebut untuk digunakan sebagai alat prediksi.
Kesalahan baku koefisien regresi (b) yaitu mengukur tingkat penyimpangan dari masing-masing koefisien regresi, dinyatakan dengan sb dan dirumuskan sebagai berikut
Semakin tinggi kesalahan baku koefisien regresi maka semakin lemah variabel tersebut untuk diikutkan dalam model persamaan regresi (semakin tidak berpengaruh).
Berdasarkan pada contoh penerapan sebelumnya diperoleh persamaan garis regresi kecepatan pertumbuhan pada frekuensi penyiraman.
Ŷ = 0,24 + 0,31X
JKG = JKT − JKR = 2,029 − 1,922 = 0,107
Sehingga kesalahan baku taksiran
Ini menunjukkan bahwa nilai pengamatan variable terikat (kecepatan pertumbuhan) menyebar dari persamaan garis regresi sekitar 0,11565.
Sedangkan kesalahan baku koefisien regresi












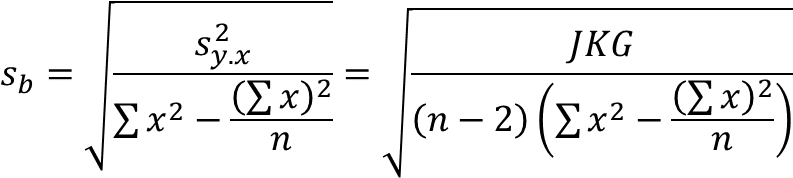




Komentar
Posting Komentar