Distribusi Geometrik (Teopro)
1. Definisi dan Formula
Misalkan sebuah eksperimen terdiri dari serangkaian percobaan dengan kondisi-kondisi berikut:
1. Percobaan-percobaan tersebut saling bebas (independen).
2. Setiap percobaan dapat menghasilkan salah satu dari dua kemungkinan hasil, yaitu sukses dan gagal.
3. Probabilitas sukses adalah sama untuk semua percobaan.
Sebuah variabel acak geometrik didefinisikan sebagai
x = banyak percobaan sampai keberhasilan pertama diamati (termasuk percobaan yang berhasil)
Distribusi probabilitas dari x disebut distribusi probabilitas geometrik.
Jika X merupakan variabel random dengan peluang sukses untuk setiap percobaan adalah p, maka
2. Fungsi Pembangkit Momen, Rerata, dan Variansi
A. Fungsi Pembangkit Momen
B. Mean dan Variansi
Sebelum menentukan mean dan variansi, kita tentukan terlebih dahulu turunan parsial pertama dan kedua dari fungsi pembangkit momen
Tentukan mean dan variansi
Mean = E[X] = 1/p
Var[X] = E[X²] − (E[X])² = (2 − p)/p² − 1/p² = (1 − p)/p²
Contoh Soal
Dua buah dadu dilempar secara bersamaan. Tentukan probabilitas bahwa jumlah kedua matadadu adalah 7 terjadi sebelum lemparan kelima.
A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}; n(A) = 6
n(S) = 6 × 6 = 36.
p = 6/36 = ⅙; 1 − p = 1 − ⅙ = ⅚
P[X < 5] = f(1) + f(2) + f(3) + f(4)
= ⅙ + ⅙.⅚ + ⅙.(⅚)² + ⅙.(⅚)³
= 671/1296 ≈ 0,517747
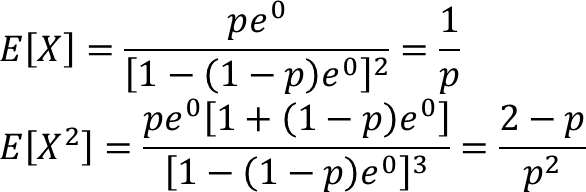
Komentar
Posting Komentar