Estimasi Interval: Konsep Dasar dan Prosedur Umum
1. Konsep Dasar dan Bentuk Umum
Untuk menentukan estimasi interval dari θ, harus ditentukan dua nilai batas θₘᵢₙ dan θₘₐₓ sedemikian hingga
P(θₘᵢₙ ≤ θ ≤ θₘₐₓ) = 1 − α
dimana α adalah taraf signifikansi, sedangkan 1 − α adalah taraf konfidensi.
Estimasi interval untuk θ dengan taraf signifikansi α adalah θₘᵢₙ ≤ θ ≤ θₘₐₓ.
2. Prosedur Umum
A. Prosedur Umum
Misal ingin ditentukan estimasi interval untuk θ, berikut prosedurnya secara umum:
1. Tentukan estimasi titik dari θ dan distribusinya
2. Tentukan besaran pivot, yaitu besaran yang memuat θ dan θ̂ sehingga distribusinya tidak tergantung pada θ; juga tentukan distribusi dari pivot
3. Misal pivotnya adalah Q, masukkan ke bentuk umum estimasi interval, yaitu
P(a ≤ Q ≤ b) = 1 − α
4. Uraikan sehingga diperoleh bentuk
P(c ≤ θ ≤ d) = 1 − α
B. Margin of Error (E)
Khusus untuk distribusi simetris, ada istilah margin of error (E), yang mana pada bentuk
P(c ≤ θ ≤ d) = 1 − α
margin of error dirumuskan:
• E = θ − c = d − θ = ½(d − c)
• d − c = 2E
• c = θ̂ − E
• d = θ̂ + E
untuk distribusi simetris, perhitungan agak lebih mudah, dengan adanya margin of error. Bentuk estimasi interval untuk distribusi simetris adalah:
θ̂ − E ≤ θ ≤ θ̂ + E
C. Distribusi Simetris
Diantara distribusi yang simetris:
• Distribusi Normal, X~N(μ, σ²), simetris terhadap garis x = μ
• Distribusi Student, X~t(v), simetris terhadap garis x = 0
• Distribusi Uniform (baik diskrit maupun kontinu), simetris terhadap mediannya
dan lain-lain.
Contoh Soal
1. Misal X₁, X₂, ..., Xₙ merupakan sampel random dari VR X~N(μ, σ²), tentukan estimasi interval untuk μ.
a. Estimasi Titik
Pada pembahasan estimasi titik, kita telah mendapati bahwa μ̂ = x̄
juga x̄~N(μ, σ²/n)
b. Pivot
Pada pembahasan distribusi fungsi VR, kita telah mendapati bahwa transformasi dari X~N(μ, σ²) menjadi Y = (x − μ)/σ memiliki distribusi yang tidak tergantung pada μ, dimana Y~N(0, 1).
Lakukan cara yang sama pada x̄, diperoleh pivotnya
P[−zα/2 ≤ z ≤ zα/2] = 1 − α
d. Interval Parameter
jadi, estimasi interval untuk μ adalah
distribusinya simetris, margin of error dari μ adalah
2. Misal X₁, X₂, ..., Xₙ merupakan sampel random dari VR X yang terdistribusi normal tetapi σ² tidak diketahui, tentukan estimasi interval untuk μ.
distribusinya simetris, margin of error dari μ adalah
2. Misal X₁, X₂, ..., Xₙ merupakan sampel random dari VR X yang terdistribusi normal tetapi σ² tidak diketahui, tentukan estimasi interval untuk μ.
a. Estimasi Titik
Estimasi titik untuk μ adalah x̄, akan tetapi variansi populasi tidak diketahui, sehingga tidak memungkinkan menyatakan x̄ menggunakan distribusi normal. Sebagai gantinya, gunakan distribusi t yang tidak memerlukan diketahui variansi populasi, juga distribusi t akan semakin mendekati distribusi normal tergantung dari banyaknya sampel.
x̄~t(n − 1).
b. Pivot
Untuk ini, pivotnya adalah dengan menggunakan variansi sampel sebagai ganti dari variansi populasi.
d. Interval Parameter
3. Misal X₁₁, X₁₂, ..., X₁n1 merupakan sampel random dari VR X₁~N(μ1, σ1²), dan X₂₁, X₂₂, ..., X₂n2 merupakan sampel random dari VR X₂~N(μ2, σ2²), tentukan estimasi interval untuk μ₁ − μ₂.
a. Estimasi Titik
Estimasi titik untuk μ₁ adalah x̄₁ dan untuk μ₂ adalah x̄₂, sehingga estimasi titik untuk μ₁ − μ₂ adalah
x̄₁ − x̄₂.
Untuk menentukan distribusinya, tentukan fungsi pembangkit momen
Karena berdistribusi normal dan variansi diketahui, gunakan bilangan baku sebagai pivot.
c. Interval Pivot
P[−zα/2 ≤ z ≤ zα/2] = 1 − α
d. Interval Parameter
jadi, estimasi interval untuk μ₁ − μ₂ adalah
distribusinya simetris, margin of error dari μ₁ − μ₂ adalah
distribusinya simetris, margin of error dari μ₁ − μ₂ adalah
4. Misal X₁₁, X₁₂, ..., X₁n1 merupakan sampel random dari VR X₁ yang berdistribusi normal, dan X₂₁, X₂₂, ..., X₂n2 merupakan sampel random dari VR X₂ yang berdistribusi normal, sedangkan variansi dari masing-masing tidak diketahui tentukan estimasi interval untuk μ₁ − μ₂.
a. Estimasi Titik
Estimasi titik untuk μ₁ adalah x̄₁ dan untuk μ₂ adalah x̄₂, sehingga estimasi titik untuk μ₁ − μ₂ adalah
x̄₁ − x̄₂.
akan tetapi variansi masing-masing populasi tidak diketahui, sehingga tidak memungkinkan menyatakan x̄₁ − x̄₂ menggunakan distribusi normal. Sebagai gantinya, gunakan distribusi t yang tidak memerlukan diketahui variansi populasi, juga distribusi t akan semakin mendekati distribusi normal tergantung dari banyaknya sampel.
(x̄₁ − x̄₂)~t(n₁ + n₂ − 2)
b. Pivot
Untuk ini, pivotnya adalah dengan menggunakan variansi sampel sebagai ganti dari variansi populasi.
jadi, estimasi interval untuk μ₁ − μ₂ adalah
distribusinya simetris, margin of error dari μ₁ − μ₂ adalah
5. Misal X₁, X₂, ..., Xₙ merupakan sampel random dari VR X~Exp(θ), tentukan estimasi interval untuk θ.
a. Estimasi Titik
Pada pembahasan estimasi titik, kita telah mendapati bahwa θ̂ = x̄. Perhatikan bahwa
fungsi pembangkit momen ini bukanlah FPM dari distribusi apapun, akan tetapi mendekati distribusi chi-square. Kita bisa membawanya kepada distribusi chi-square dengan mengalikan x̄ dengan 2n/θ, sehingga 2nx̄/θ berdistribusi chi-square.
b. Pivot
Menurut poin (a), kita bisa memilih 2nx̄/θ sebagai pivot.
𝜒² = 2nx̄/θ
c. Interval Pivot
P[𝜒²1−α/2;2n ≤ 𝜒² ≤ 𝜒²α/2;2n] = 1 − α
d. Interval Parameter
P[𝜒²1−α/2;2n ≤ 2nx̄/θ ≤ 𝜒²α/2;2n] = 1 − α
P[2nx̄/𝜒²α/2;2n ≤ θ ≤ 2nx̄/𝜒²1−α/2;2n] = 1 − α
jadi, estimasi interval untuk θ adalah
6. Misal X₁, X₂, ..., Xₙ merupakan sampel random dari VR X~N(μ, σ²), tentukan estimasi interval untuk σ².
a. Estimasi Titik
Pada pembahasan estimasi titik, kita telah mendapati bahwa estimator takbias untuk σ² adalah
bentuk ini masih belum diketahui distribusinya. Akan tetapi ingat kembali bahwa Z = (x − μ)/σ berdistribusi N(0, 1).
b. Pivot
Misal Y = Z², berikut fungsi distribusi kumulatif dari Y:
∑Y~𝜒²(n).
𝜒² = ∑Y = ∑Z² ini dipilih sebagai pivot.
𝜒² = ∑Y = ∑Z² ini dipilih sebagai pivot.
c. Interval Pivot
P[𝜒²1−α/2;n ≤ 𝜒² ≤ 𝜒²α/2;n] = 1 − α
d. Interval Parameter
P[𝜒²1−α/2;n ≤ ∑Z² ≤ 𝜒²α/2;n] = 1 − α





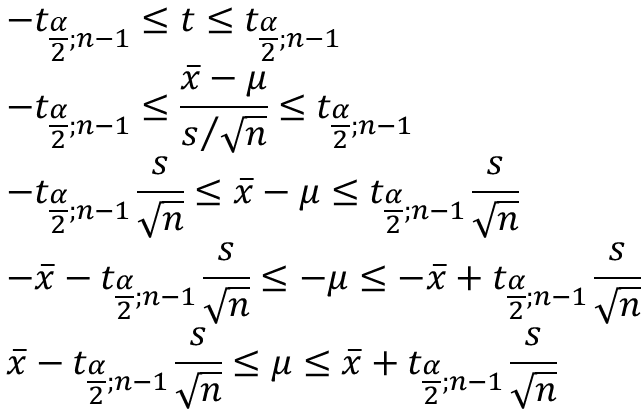



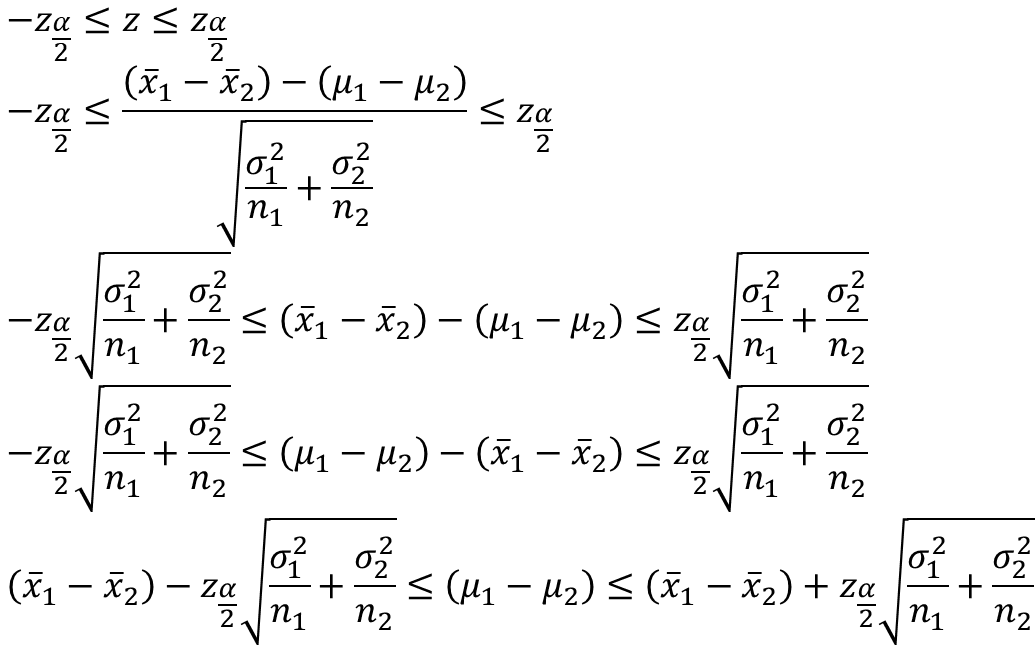

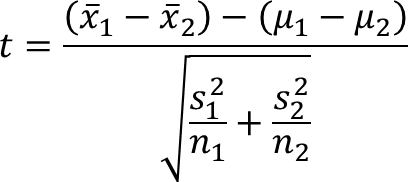














Komentar
Posting Komentar