Uji Hipotesis (Statmat)
Ilustrasi:
Misalkan seorang petani melakukan suatu eksperimen untuk melihat pupuk A atau B yang paling baik untuk pertumbuhan suatu tanaman X.
▪ Penelitian 1 menyatakan bahwa pupuk A dapat menumbuhkan tanaman X dengan kecepatan 4cm per pekan setelah diberikan pupuk.
▪ Penelitian 2 menyatakan bahwa pupuk B dapat menumbuhkan tanaman X dengan kecepatan 2cm per pekan setelah diberikan pupuk.
Dengan menggunakan teori, referensi, dan hasil penelitian yang relevan, petani tersebut menduga bahwa pupuk A lebih baik dari pupuk B untuk menumbuhkan tanaman X.
1. Hipotesis Statistik
Hipotesis merupakan pernyataan atau dugaan mengenai nilai suatu parameter θ, yang dituliskan dalam bentuk:
H₀: θ ∈ ω vs H₁: θ ∉ ω; dengan ω ⊂ Ω.
Pada umumnya untuk ruang lengkap, Ω = {θ | θ ∈ ℝ} = ℝ. Akan tetapi terkadang adakalanya Ω bukanlah ruang lengkap, dimana Ω ⊂ ℝ.
Berikut ini formulasi hipotesis untuk ruang lengkap:
• Formulasi hipotesis dua pihak
H₀: θ = θ₀ vs H₁: θ ≠ θ₀
• Formulasi hipotesis pihak kanan
H₀: θ ≤ θ₀ vs H₁: θ > θ₀
• Formulasi hipotesis pihak kiri
H₀: θ ≥ θ₀ vs H₁: θ < θ₀
2. Hipotesis Sederhana dan Hipotesis Komposit
• Hipotesis sederhana adalah hipotesis yang hanya memungkinkan satu nilai
Bentuk umum: θ = θ₀
Pada bentuk ini hanya ada satu kemungkinan nilai θ, yaitu θ₀.
• Hipotesis komposit adalah hipotesis yang memungkinkan lebih dari satu nilai
Bentuk-bentuk umum: θ ≠ θ₀, θ ≤ θ₀, θ ≥ θ₀, θ > θ₀, θ < θ₀
Pada bentuk-bentuk ini masing-masing memiliki kemungkinan lebih dari satu nilai untuk θ.
3. Daerah Kritis
Misal ruang variabel random (Ω) dipartisi menjadi dua bagian C dan C*, dengan:
• C merupakan daerah dimana H₀ ditolak, daerah ini disebut sebagai daerah kritis
• C* merupakan daerah dimana H₀ tidak ditolak
Jadi, daerah kritis adalah daerah dimana H₀ ditolak.
4. Kesalahan Uji
Suatu pengujian hipotesis bisa saja mengalami kesalahan, berikut tipe kesalahannya:
A. Kesalahan Tipe I
Kesalahan tipe I adalah menolak H₀ padahal H₀ benar, dituliskan (x₁, x₂, ..., xₙ) ∈ C : H₀.
Peluang melakukan kesalahan tipe I disimbolkan dengan α.
α = P[(x₁, x₂, ..., xₙ) ∈ C : H₀], dinamakan tingkat signifikan.
1 – α = P[(x₁, x₂, ..., xₙ) ∈ C* : H₀], dinamakan tingkat konfidensi.
B. Kesalahan Tipe II
Kesalahan tipe II adalah tidak menolak H₀ padahal H₀ salah, dituliskan (x₁, x₂, ..., xₙ) ∈ C* : H₁.
Peluang melakukan kesalahan tipe II disimbolkan dengan β.
β = P[(x₁, x₂, ..., xₙ) ∈ C* : H₁], tidak memiliki nama khusus.
1 – β = P[(x₁, x₂, ..., xₙ) ∈ C : H₁], dinamakan kuasa uji.
C. Sifat dari Kesalahan Tipe I dan Tipe II
1. Kesalahan tipe I dan II saling terkait, yaitu memperkecil nilai α akan memperbesar nilai β dan sebaliknya.
2. Ukuran tingkat signifikansi, yaitu α, dapat selalu diperkecil dengan menyesuaikan nilai kritisnya.
3. Menaikan ukuran sampel akan memperkecil nilai α maupun β.
Contoh Soal
1. Misal X₁, X₂, ..., Xₙ sampel random dari VR X~N(⅔θ, 9). Akan dilakukan uji hipotesis
H₀: θ = 6 vs H₁: θ ≠ 6
1a. Tentukan nilai k, sehingga α = 5% dan C = {(x₁, x₂, ..., x₈₁): (x̄ – 4)² > k}
5% = α = P[(x₁, x₂, ..., xₙ) ∈ C : H₀] = P[(x̄ – 4)² > k : H₀]
Karena simetris,
Jadi, nilai k adalah 0,42683; sehingga C = {(x₁, x₂, ..., x₈₁): (x̄ – 4)² > 0,42683}
Jadi, nilai k adalah 0,42683; sehingga C = {(x₁, x₂, ..., x₈₁): (x̄ – 4)² > 0,42683}
1b. Tentukan banyak sampel sehingga α = 2% dan C = {(x₁, x₂, ..., xₙ): |x̄ – 4| > 0,5}
2% = α = P[(x₁, x₂, ..., xₙ) ∈ C : H₀] = P[|x̄ – 4| > 0,5 : H₀] = P[x̄ – 4 < –0,5 ∨ x̄ – 4 > 0,5 : H₀]
2. Misal X₁, X₂, ..., Xₙ sampel random dari VR X~N(𝜇, 36). Akan dilakukan uji hipotesis
H₀: 𝜇 = 50 vs H₁: 𝜇 = 55
Tentukan tingkat signifikansi dan kuasa uji jika daerah kritisnya adalah
C = {(x₁, x₂, ..., x₁₆) : x̄ ≥ 53}
2a. Tingkat signifikansi
Perhatikan
α = P[(x₁, x₂, ..., xₙ) ∈ C : H₀] = P[x̄ ≥ 53 : 𝜇 = 50]
2b. Kuasa uji
1 – β = P[(x₁, x₂, ..., xₙ) ∈ C : H₁] = P[x̄ ≥ 53 : 𝜇 = 55]



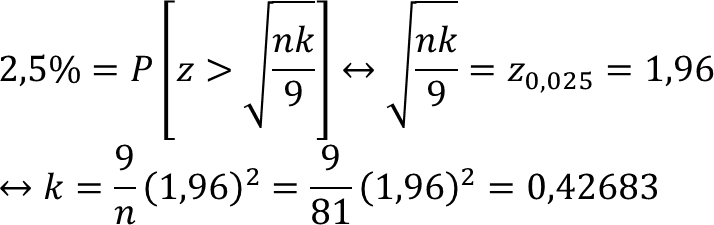



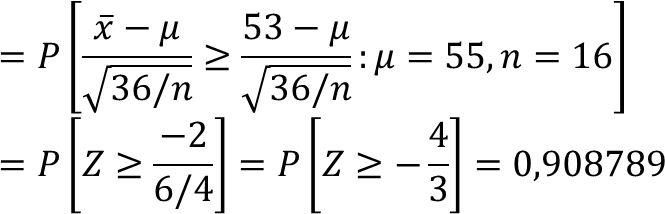


Komentar
Posting Komentar