Sixty Four Science

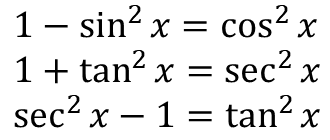
Ingat kembali identitas trigonometri berikut: Bentuk-bentuk ini dapat disubstitusikan trigonometri sebagai: Untuk bentuk selisih kuadrat konstanta dikurangi variabel gunakan substitusi sinus. Untuk bentuk selisih kuadrat variabel dikurangi konstanta gunakan substitusi sekan. Untuk bentuk jumlah kuadrat gunakan substitusi tangen. contoh untuk substitusi sinus: sampai sini diperoleh bentuk selisih kuadrat konstanta dikurangi variabel, kita dapat mengambil substitusi sinus untuk mengubahnya menjadi bentuk trigonometri kembalikan ke variabel sebelumnya contoh untuk substitusi sekan: sampai sini diperoleh bentuk selisih kuadrat variabel dikurangi konstanta, kita dapat mengambil substitusi sekan untuk mengubahnya menjadi bentuk trigonometri sampai bentuk ini dapat dipisahkan kembalikan ke variabel asal contoh untuk substitusi tangen: sampai sini diperoleh bentuk jumlah kuadrat, kita dapat mengambil substitusi tangen untuk mengubahnya menjadi bentuk trigonometri kembalikan ke variabel asal

1. Integral Fungsi Sinus dan Kosinus Berpangkat A. Fungsi Sinus dan Kosinus Berpangkat Ganjil Untuk pangkat ganjil, ambil satu pangkat untuk substitusi, bentuk umum: contoh: dengan ini bisa mengambil substitusi: B. Fungsi Sinus dan Kosinus Berpangkat Genap Ingat identitas trigonometri kosinus sudut rangkap: dengan melakukan pemindahan ruas, akan diperoleh: contoh: 2. Integral Hasil Kali Sinus dengan Kosinus Berpangkat Ingat identitas ini, barangkali terpakai: A. Keduanya Berpangkat Genap Ambil salah satu untuk diterapkan aturan genap, contoh: selesaikan satu persatu, untuk yang berpangkat 4 sudah dibahas sebelumnya: untuk yang berpangkat 6: hasil akhirnya adalah: bisa juga menggunakan identitas sinus rangkap: B. Salahsatu atau Keduanya Berpangkat Ganjil Untuk kasus dimana salahsatu berpangkat ganjil, ambil satu pangkat dari yang ganjil untuk substitusi, contoh: Adapun untuk kasus dimana keduanya berpangkat ganjil, bisa memilih salahsatu untuk disubstitusikan. 3. Integral Hasil Kali Sin...

1. Integral Fungsi Invers Trigonometri Berikut integral fungsi invers sinus: Berikut integral fungsi invers kosinus: Berikut integral fungsi invers tangen: Berikut integral fungsi invers kotangen: Berikut integral fungsi invers sekan: Berikut integral fungsi invers kosekan: All in one integral fungsi invers trigonometri: 2. Integral Fungsi Invers Hiperbolik Sebelum membahas integral fungsi invers hiperbolik, ingat kembali fungsi invers hiperbolik: Ingat juga integral fungsi hiperbolik: Berikut integral fungsi invers sinus hiperbolik: Berikut integral fungsi invers kosinus hiperbolik: Berikut integral fungsi invers tangen hiperbolik: Berikut integral fungsi invers kotangen hiperbolik: Berikut integral fungsi invers kosekan hiperbolik: Berikut integral fungsi invers sekan hiperbolik: All in one integral fungsi invers hiperbolik: