Kejadian Bersyarat dan Partisi (Stadas)
1. Kejadian bersyarat
A. Untuk 2 kejadian
Kejadian B dengan syarat kejadian A adalah terjadinya kejadian B jika kejadian A telah terjadi, dinotasikan dengan B | A.
Jika A dan B dua kejadian dalam ruang sampel S dengan P(A) ≠ 0, maka peluang kejadian B jika diketahui kejadian A didefinisikan sebagai :
yang mana ekivalen dengan:
𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴) × 𝑃(𝐵 | 𝐴)
Misalkan dalam sebuah kotak terdapat 6 bola kuning dan 4 bola hitam. Dua bola akan diambil berturut-turut tanpa dikembalikan. Tentukan peluang diperolehnya bola hitam pada pengambilan pertama dan bola kuning pada pengambilan kedua!
Peluang diperolehnya bola hitam pada pengambilan pertama = 4/10 = ⅖
Setelah terambil bola hitam pada pengambilan pertama, dan tidak dikembalikan lagi, banyak bola dalam kotak tersisa 9, sehingga n(S) = 9, sehingga:
Peluang diperolehnya bola kuning pada pengambilan kedua = 6/9 = ⅔
Sehingga
𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴) × 𝑃(𝐵 | 𝐴) = ⅖ × ⅔ = 4/15
B. Perluasan untuk lebih dari 2 kejadian
Jika A1, A2, A3, … kejadian-kejadian dalam ruang sampel S, maka
Ingat kembali tentang partisi himpunan. Kita dapat mendefinisikan partisi sebagai:
Himpunan A1, A2, A3, …, Ak membentuk partisi dalam ruang sampel 𝑆 jika:
1. Gabungan seluruh partisi adalah S
2. Irisan masing-masing sepasang adalah himpunan kosong
Ai ∩ Aj = ∅ untuk setiap 1 ≤ i ≤ k, 1 ≤ j ≤ k, i ≠ j
Ai ∩ Aj = ∅ untuk setiap 1 ≤ i ≤ k, 1 ≤ j ≤ k, i ≠ j
Ilustrasi untuk partisi:
Peluang Total
Jika kejadian B1, B2, B3, …, Bk membentuk partisi di dalam ruang sampel S dan 𝑃(Bi) ≠ 0 untuk 𝑖 = 1, 2, 3, …, 𝑘, maka untuk sembarang kejadian A didalam S dengan 𝑃(𝐴) ≠ 0 berlaku:
Misal terdapat 3 kotak berisi lampu, dengan:
• Kotak 1 berisi 12 lampu, dengan 4 rusak
• Kotak 2 berisi 10 lampu, dengan 3 rusak
• Kotak 3 berisi 8 lampu, dengan 2 rusak
Akan diambil lampu secara acak dari kotak yang ditentukan berdasarkan matadadu:
• Diambil dari kotak 1 untuk matadadu bilangan prima (2, 3, 5)
• Diambil dari kotak 2 untuk matadadu bilangan komposit (4, 6)
• Diambil dari kotak 3 untuk matadadu 1
Peluang terambilnya lampu rusak adalah:
P(R) = P(K1).P(R | K1) + P(K2).P(R | K2) + P(K3).P(R | K3)
3. Teorema Bayes
Jika kejadian B1, B2, B3, …, Bk membentuk partisi di dalam ruang sampel S dan 𝑃(Bi) ≠ 0 untuk 𝑖 = 1, 2, 3, …, 𝑘, maka untuk sembarang kejadian A didalam S dengan 𝑃(𝐴) ≠ 0 berlaku:
kembali ke masalah lampu rusak, jika terambil 1 lampu rusak, maka peluang terambil dari kotak 2 adalah:
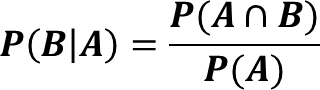







Komentar
Posting Komentar