Metode Momen untuk Estimasi Titik
Misalkan X adalah variabel random dengan fungsi densitas probabilitas f(x) dan parameter populasi θ, maka untuk sampel random X1, X2, ..., Xn statistik θ̂ = g(X1, X2, ..., Xn) dinamakan estimator dari θ.
Terdapat berbagai macam metode untuk menentukan estimasi titik, diantaranya:
1. Metode Momen
2. Metode Maximum Likelihood
dan lain-lain. Disini akan kita bahas metode momen.
Berikut langkah-langkah menentukan estimator menggunakan metode momen:
1. Tentukan momen populasi
Momen ke-t dari populasi didefinisikan:
μt = E(Xt)
dengan t = 1, 2, ..., k (sebanyak k momen)
2. Tentukan momen sampel
Momen ke-t dari sampel didefinisikan:
Setelah diperoleh momen-momen populasi dan sampel, samakan setiap momen yang bertepatan.
μt = mt; t = 1, 2, ..., k
Contoh Soal
1. FDP dari distribusi Poisson dari VR X dengan parameter λ adalah
tentukan estimator untuk λ.
a. Momen populasi
μ1 = E(X) = λ
b. Momen sampel
λ̂ = x̄
Jadi, estimator untuk λ adalah x̄
2. FDP dari distribusi Normal dari VR X dengan parameter μ dan σ² adalah
tentukan estimator untuk μ dan σ².
a. Momen populasi
μ1 = E(X) = μ
μ2 = E(X²) = 𝜎² + 𝜇²
𝜎² = μ2 − (μ1)²
b. Momen sampel
m1 = x̄
Estimator untuk μ2 adalah m2
sehingga estimator untuk 𝜎² adalah m2 − (m1)², yaitu
tentukan estimator untuk θ.
a. Momen populasi
μ1 = E(X) = θ
b. Momen sampel
m1 = x̄
c. Samakan momen populasi dan momen sampel
θ̂ = x̄
4. FDP dari distribusi Binomial dari VR X dengan parameter p adalah
a. Momen populasi
μ1 = E(X) = np ↔ p = μ1/n
b. Momen sampel
m1 = x̄
c. Samakan momen populasi dan momen sampel
μ1 = m1
p̂ = m1/n = x̄/n
jadi, estimator untuk p adalah x̄/n.





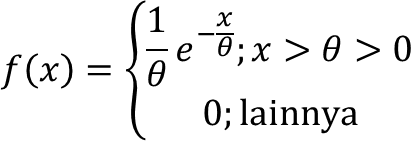



Komentar
Posting Komentar