Estimator Efisien
θ̂ = g(X1, X2, ..., Xn) merupakan estimator yang baik dari θ jika memenuhi ketiga kriteria:
1. Tak bias (tepat sasaran)
2. Konsisten (tidak berubah-ubah)
3. Efisien
Disini kita akan membahas estimator efisien.
Jika θ̂₁ dan θ̂₂ merupakan estimator tak bias bagi θ, maka θ̂₁ dikatakan estimator efisien bagi parameter θ jika Var(θ̂₁) < Var(θ̂₂).
Jika terdapat beberapa estimator tak bias bagi θ, maka estimator efisien ditentukan yang mempunyai variansi minimum. Untuk keperluan tersebut dapat memanfaatkan batas bawah Cramer-Rao sebagai berikut:
1. Variabel random X berdistribusi Poisson dengan parameter λ, apakah estimator λ̂ = x̄ efisien?
Untuk menentukan batas bawah Cramer-Rao, mula-mula ingat kembali FDP VR X:
tarik logaritma
ln(f(x)) = −λ + x.ln(λ) − ln(x!)
turunankan 2 kali terhadap λ
2. VR X berdistribusi Binomial dengan parameter p, apakah estimator p̂ = x̄/n efisien?
Untuk menentukan batas bawah Cramer-Rao, mula-mula ingat kembali FDP VR X:
tarik logaritma
turunkan terhadap p dua kali
tentukan ekspektasi turunan parsial kedua
tentukan BBCR
Var[p̂] = BBCR, ini berarti p̂ merupakan estimator efisien untuk p.
tentukan ekspektasi turunan parsial kedua
tentukan BBCR
Var[p̂] = BBCR, ini berarti p̂ merupakan estimator efisien untuk p.
3. Variabel random X berdistribusi Eksponensial dengan parameter θ, apakah estimator θ̂ = x̄ efisien?











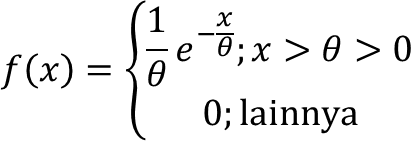





Komentar
Posting Komentar