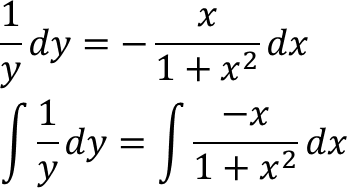Sixty Four Science

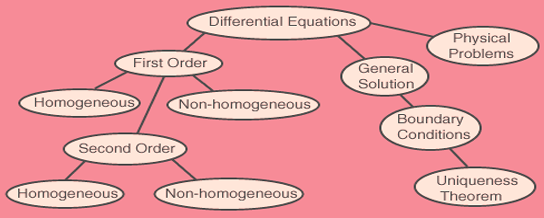
Persamaan diferensial linier orde satu dengan variabel terikat y dan variabel bebas x, dapat ditulis dalam bentuk: dy/dx + P(x)⋅y = Q(x) Bentuk lain [P(x)⋅y − Q(x)]dx + dy = 0 Perdif linier orde satu memiliki faktor integral μ(x) = exp[∫P(x) dx] Langkah-langkah untuk menyelesaikan Persamaan Diferensial Linier Orde satu adalah sebagai berikut: 1. Nyatakan perdif linier orde 1 dalam bentuk standar dy/dx + P(x)⋅y = Q(x) 2. Tentukan faktor integral μ(x) = exp[∫P(x) dx] 3. Bentuk persamaan y.μ(x) = ∫μ(x).Q(x) dx + C Contoh Soal 1. (x)dy/dx + (x + 1)y = x³ bagi masing-masing ruas dengan x dy/dx + (1 + 1/x)y = x² P(x) = 1 + 1/x, Q(x) = x² μ(x) = exp[∫P(x) dx] = exp[∫1 + 1/x dx] = exp(x + ln(x)) = x⋅exp(x); untuk x > 0 y.μ(x) = ∫μ(x).Q(x) dx + C y = x² − 3x + 6 − 6/x + C/x 2. dy/dx + 3y/x = 6x² P(x) = 3/x, Q(x) = 6x² μ(x) = exp[∫P(x) dx] = exp[∫3/x dx] = exp[3.ln(x)] = x³ y.μ(x) = ∫μ(x).Q(x) dx + C y.x³ = ∫x³.6x² dx + C = ∫6x⁵ dx + C = x⁶ + C y = x³ + C/x³ 3. dy/dx + 3y = 3x²⋅exp(−3x) P(x) ...

Bentuk umum Perdif non homogen bentuk khusus: (ax + by + c)dx + (px + qy + r)dy = 0 terdapat 3 kondisi: • a/p = b/q = c/r • a/p = b/q ≠ c/r • a/p ≠ b/q 1. Perdif Non Homogen Bentuk Khusus dengan a/p = b/q = c/r Misal suatu Perdif (ax + by + c)dx + (px + qy + r)dy = 0 dengan a/p = b/q = c/r = λ Misal px + qy + r = u ↔ ax + by + c = λu, perdif menjadi λu dx + u dy = 0, bagi masing-masing ruas dengan u λ dx + dy = 0 ∫λ dx + ∫dy = 0 λx + y = C Jadi, hasil akhirnya adalah λx + y = C. 2. Perdif Non Homogen Bentuk Khusus dengan a/p = b/q  ≠  c/r Misal suatu Perdif (ax + by + c)dx + (px + qy + r)dy = 0 dengan a/p = b/q ≠ c/r Misal a/p = b/q = μ; px + qy = u → p dx + q dy = du ↔ dy = (du − p dx)/q perdif menjadi (μu + c)dx + (u + r)(du − p dx)/q = 0, kalikan q (μuq + cq − pu − pr)dx + (u + r)du = 0 dx = −(u + r)/(μuq + cq − pu − pr) du bentuk terakhir ini separabel. 3. Perdif Non Homogen Bentuk Khusus dengan a/p ≠ b/q Misal suatu Perdif...

1. Fungsi Homogen Misal f fungsi dua variabel x dan y, fungsi f dikatakan homogen berderajat n jika berlaku: f(kx, ky) = kⁿ.f(x, y); k ∈ ℝ contoh: f(x, y) = x² + 3xy + 2y², masukkan kx dan ky f(kx, ky) = (kx)² + 3(kx)(ky) + 3(ky)² = k²x² + 3k²xy + 2k²y² = k²(x² + 3xy + 2y²) fungsi ini merupakan fungsi homogen berderajat 2. 2. Persamaan Diferensial Homogen Persamaan diferensial berbentuk M(x, y) dx + N(x, y) dy = 0 dikatakan homogen jika M(x, y) dan N(x, y) keduanya fungsi homogen berderajat sama. 3. Langkah Menyelesaikan Perdif Homogen Misal suatu Perdif berbentuk M(x, y) dx + N(x, y) dy = 0 homogen, berikut langkah penyelesaiannya: 1. Misalkan y = vx → dy = v dx + x dv, akan membentuk Perdif separabel dalam v dan x. 2. Selesaikan Perdif separabel yang terbentuk. 3. Kembalikan ke bentuk semula, yaitu v = y/x. Catatan: Perlu berhati-hati dengan Perdif yang mana M(x, y) dan N(x, y) keduanya fungsi homogen tetapi derajatnya berbeda, karena tidak bisa diselesaikan menggunakan meto...

Untuk Persamaan Diferensial Separabel orde satu yang berbentuk y′ = f(x), dimana f fungsi kontinu dari satu variabel bebas x, maka kita dapat mengintegralkan secara langsung kedua ruas untuk memperoleh penyelesainnya. Bentuk umum: dy/dx = f(x, y) Untuk mencari penyelesaian umum dari persamaan diferensial separabel, terlebih dahulu kita pisahkan variabel x dan y, sehingga kita peroleh fungsi f(x, y) = p(x).q(y) Contoh 1. (xy)dx + (1 + x²)dy = 0 (1 + x²)dy = (−xy)dx Misal u = 1 + x²; du = 2x dx; −½du = −x dx eksponenkan kedua ruas 2.  Bentuk ini juga merupakan Perdif separabel, coba faktorkan masing-masing pembilang dan penyebut. integralkan masing-masing ruas Misal u = 4 + y ↔ y = u − 4 → du = dy v = 1 − x² → dv = −2x dx ↔ −½dv = x dx kembalikan ke bentuk semula 4 + y − 4⋅ln|4 + y| + C₁ = −½⋅ln|1 − x²| + C₂ y − 4⋅ln|4 + y| + ½⋅ln|1 − x²| = C₃ 3. dy/dx = cot(x)⋅tan(y) cot(y) dy = cot(x) dx ∫cot(⁡y) dy = ∫cot(⁡x) dx ln|sin(y)| + C₁ = ln|sin(x)| + C₂ ln|sin(y)| = ln|sin(...

Balai Pengembangan Talenta Indonesia (BPTI) setiap tahun menyelenggarakan Olimpiade Nasional bidang Matematika dan Ilmu Pengetahuan Alam Perguruan Tinggi (ONMIPA-PT) untuk mengembangkan talenta dan prestasi mahasiswa di bidang sains, riset, dan teknologi. ONMIPA-PT merupakan salah satu upaya untuk memenuhi kebijakan Merdeka Belajar Kampus Merdeka (MBKM) dan Indeks Kinerja Utama (IKU) perguruan tinggi, yaitu memfasilitasi mahasiswa untuk berprestasi di berbagai kompetisi. ONMIPA-PT diharapkan dapat menumbuhkan kecintaan pada Matematika dan IPA, menemukan talenta-talenta terbaik di bidang ini, serta mendorong kualitas pembelajaran dan prestasi perguruan tinggi. ONMIPA-PT diselenggarakan untuk meningkatkan penguasaan Matematika dan IPA. Penguasaan MIPA penting untuk mendorong daya saing bangsa dalam pengembangan sains dan teknologi. ONMIPA-PT telah diselenggarakan sejak tahun 2009 dan terdiri dari tiga tahap seleksi, yaitu seleksi tingkat perguruan tinggi, tingkat wilayah, dan tingkat nas...

1. Persamaan Diferensial Persamaan diferensial adalah suatu persamaan yang menyatakan hubungan fungsi yang tidak di ketahui dan turunan-turunannya. Misalkan f(x) mendefinisikan sebuah fungsi dari x pada suatu interval I[a, b] dimana a ≤ x ≤ b. Persamaan diferensial adalah persamaan yang memuat derivatif dari f(x). Orde dari suatu persamaan diferensial adalah orde tertinggi derivatif yang termuat dalam persamaan itu. 2. Penyelesaian Persamaan Diferensial Penyelesaian suatu persamaan diferensial ialah mencari suatu fungsi yang tidak memuat turunan dan memenuhi persamaan diferensial yang diberikan. Penyelesaian dapat saja dilakukan satu atau beberapa kali integrasi. 3. Persaman Diferensial Biasa dan Parsial Jika hanya ada satu variabel bebas, maka disebut Persamaan Diferensial Biasa (PDB). Sedangkan jika persamaan memuat dua atau lebih peubah bebas, maka disebut Persamaan Diferensial Parsial (PDP). 4. Masalah Nilai Awal Misalkan kita akan mencari penyelesaian dari y = y(x) dari PDB or...

1. Prinsip Inklusi-Eksklusi A . Untuk 2 himpunan, lalu 3 himpunan Untuk sebarang dua himpunan A dan B, untuk mendapatkan banyaknya anggota gabungan kedua himpunan, setiap anggota gabungan dihitung satu kali. Ketika menghitung banyaknya anggota A dan menghitung banyaknya anggota B ada kemungkinan ada anggota kedua himpunan yang dihitung dua kali. Sehingga untuk menghindari hal tersebut dalam menghitung banyaknya anggota gabungan dua himpunan A dan B kita lakukan dengan menghitung jumlah dari banyaknya anggota A dan banyaknya anggota B dan dikurangi dengan banyaknya anggota irisan dari kedua himpunan. |A ∪ B| = |𝐴| + |B| − |𝐴 ∩ B| Contoh: Berapa banyak string biner dengan panjang 8 dimulai dengan bit 1 atau diakhiri dengan bit 00. Ingat, bahwa string biner pada setiap digitnya dapat diisi dengan 0 atau 1. |A| = Banyak string biner 8 digit dimulai dengan bit 1 = 1 × 2⁷ = 128 |B| = Banyak string biner 8 digit diakhiri dengan bit 00 = 2⁶ × 1² = 64 |𝐴 ∩ B| = 1 × 2⁵ × 1² = 32 |A ∪ B| = |𝐴...

1. Kombinasi tanpa Perulangan Kombinasi r dari n obyek berbeda adalah banyak cara mengambil r obyek dari n obyek di mana urutan tidak diperhatikan dan tidak boleh ada perulangan. Karena tidak boleh ada perulangan, diharuskan r ≤ n. Kombinasi r obyek dari n obyek dinotasikan dengan n C r     atau     C n,r     atau      C r n     atau C(n, r) Ingat kembali bahwa P(n, r) = [n × (n − 1) × (n − 2) × ... × (n − r + 1) × (n − r)!]/(n − r)! = n!/(n − r)! Dan dikarenakan urutan tidak diperhatikan, maka susunan r obyek sebanyak r! dianggap sama, sehingga rumus kombinasi adalah rumus permutasi dibagi r! C(n, r) = P(n, r)/r! = n!/[(n − r)!r!] Dari rumus ini, kita mendapati bahwa kombinasi bersifat simetris, dimana C(n, r) = C(n, n − r). contoh: 1. Berapa banyak cara memilih 3 orang dari 8 anggota OSIS untuk dikirim pelatihan kepemimpinan? Banyak cara adalah 8!/[(8 − 3)!3!] = 8!/[5!3!] = (8 × 7 × 6)/(3 × 2 × 1) = 56 Ada sebanyak 56 cara. 2. Him...